16.1. Количество движения и кинетическая энергия точки. Импульс силы.

Количество движения и кинетическая энергия являются основными динамическими характеристиками движения точки.

Количество движения материальной точки называется векторная величина , равная произведению массы точки на ее скорость. Векторнаправлен так же, как и скорость точки, т.е по касательной к ее траектории.

Кинетической энергией материальной точки называется скалярная величина , равная половине произведения массы точки на квадрат ее скорости.

Элементарным импульсом силы называется векторная величина, равная произведению силына элементарный промежуток времениdt:

Полный импульс силы за некоторый конечный промежуток времени будет

В проекциях на оси координат:

,,

Если , тоили

В проекциях на оси координат: ,,

Если к точке приложено несколько сил то их равнодействующая. Умножим обе части этого равенства наи проинтегрируем

, откуда, т.е импульс равнодействующей равен геометрической сумме импульсов всех равнодействующих на точку сил.

В проекциях на оси координат:

16.2. Теорема об изменении количества движения точки.

Пусть точка М массы mдвижется под действием сил(рисунок 1). Запишем для данной точки основное уравнение динамики (1.2)

Так как ,то основное уравнение динамики запишется в виде:

(3.1)

Равенство (3.1) выражает теорему об изменении количества движения точки в дифференциальной форме: производная по времени от количества движения точки равна геометрической сумме всех действующих на точку сил.

Пусть в момент времени t=0 скорость точки, а в момент времениtскорость точки. Разделяя переменные в равенстве и интегрируя, получим:

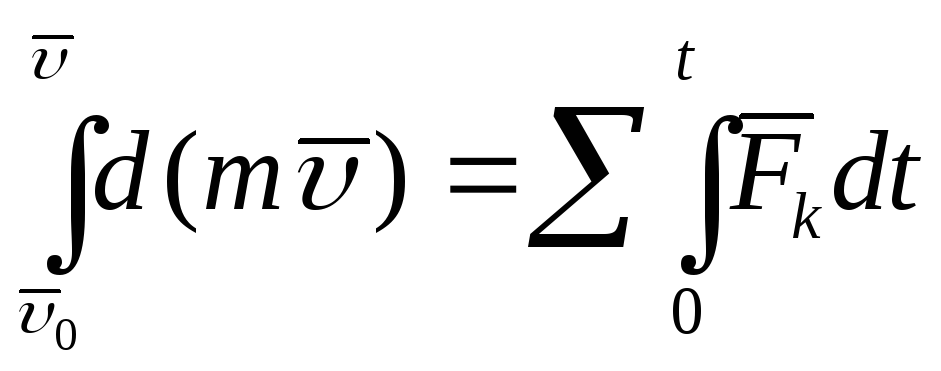
Так как , геометрической сумме импульсов сил, то

(3.2)

Равенство (3.2) выражает теорему об изменении количества движения точки в конечном виде: изменение количества движения точки за некоторый конечный промежуток времени равно геометрической сумме импульсов всех действующих на точку за тот же промежуток времени в проекциях на оси координат:

;

;

.

Теорема об изменении количества движения точки в основном применяется на тех участках траектории движения точки, на которых задано время движения точки или это время нужно определить.

16.3. Момент количества движения точки относительно центра и оси. Теорема об изменении момента количества движения точки (теорема моментов)

В некоторых задачах в качестве динамической характеристики движения точки вместо самого вектора количества движения рассматривают его момент относительно некоторого центра или оси.

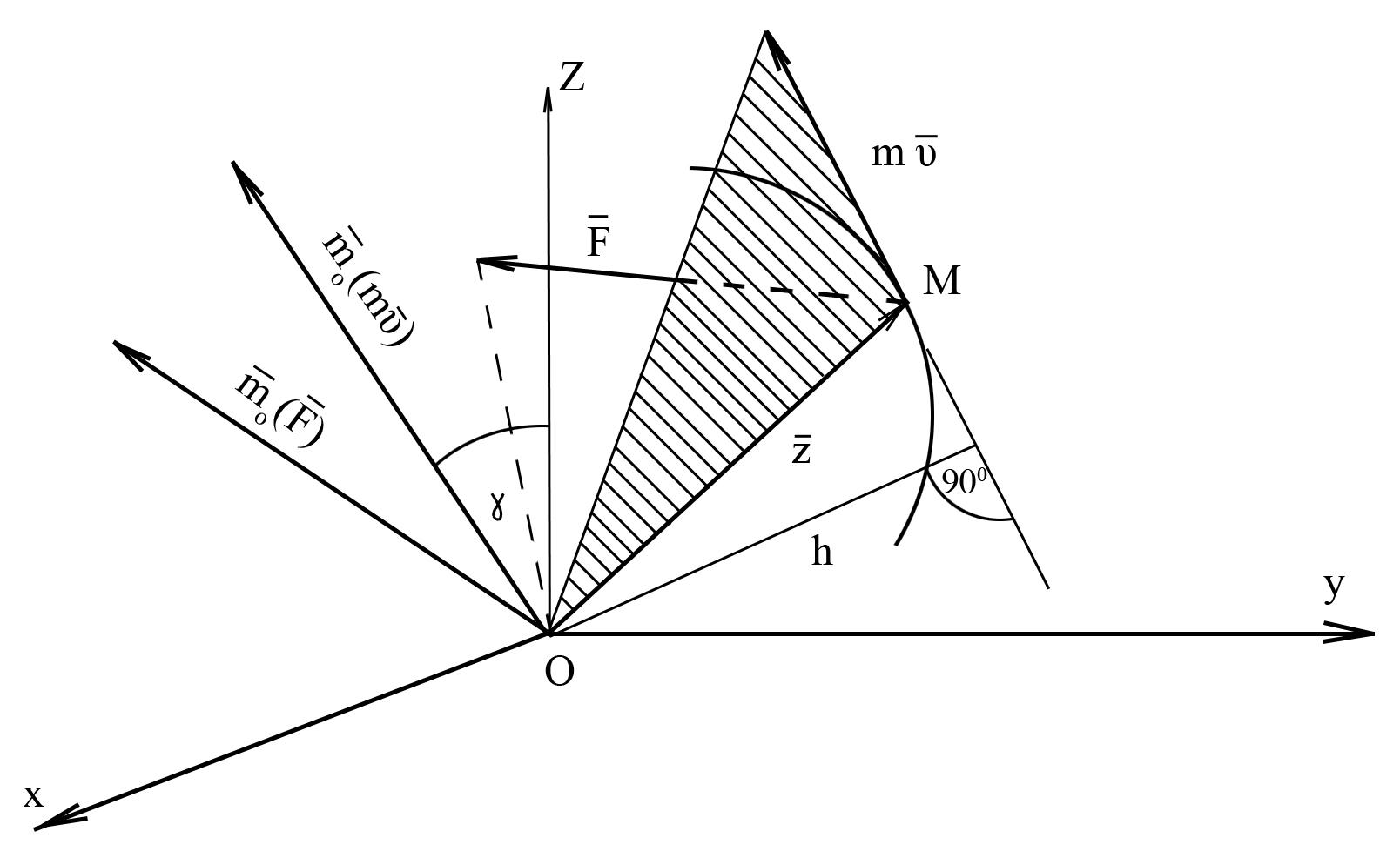
Рис. 5

Эти моменты определяются так же, как и моменты силы в статике.

Таким образом, моментом количества движения точки относительно некоторого центра О называется векторная величина , определяемая равенством:

(3.3)

где r– радиус – вектор движущейся точки М, проведенный из центра О. Векторнаправлен перпендикулярно плоскости, проходящей через вектори центр О, а(рис. 5: для сравнения на нем показан и вектор, который перпендикулярен плоскости, проходящей черези центр О)

Момент количества движения точки относительно какой-нибудь оси , проходящей через центр О, будет равен проекции вектора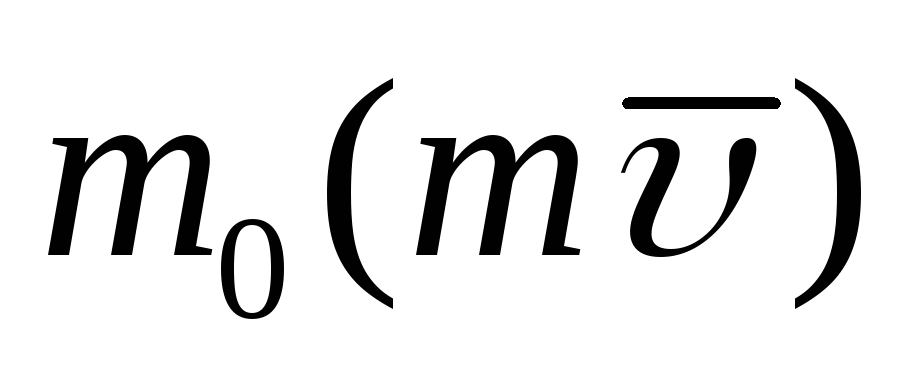на эту ось:

,

где – угол между вектороми осью.

Теорема моментов устанавливает, как изменится со временем вектор . Для доказательства продифференцируем по времени равенство (3.3) . Получим:

Но как векторное произведение двух параллельных векторов, а

Следовательно, или

(3.4)

Равенство (3.4) выражает теорему моментов относительно центра: производная по времени от момента количества движения точки, взятого относительно какого-нибудь неподвижного центра равна моменту действующей на точку силы относительно того же центра.

Проецируя равенство (3.4) на какую-нибудь ось , проходящую через центр О, получим:.

Равенство (3.5) выражает теорему моментов относительно оси

Из равенства (3.4) следует, что если , то