15.5. Интегрирование дифференциальных уравнений движения материальной точки

Вторая основная задача динамики точки является более сложной и ее рекомендуется решать по следующему плану:

15. Выбрать начало отсчета и ввести необходимую систему координат

16. показать точку в произвольном положении и изобразить все действующие на нее силы

17. составить дифференциальные уравнения движения точки на оси введенной системы координат

18. решить полученные дифференциальные уравнения.

Приведем примеры интегрирования дифференциальных уравнений движения материальной точки. Пусть точка М массы mдвижется, например, по осиxпод действием силы. Ее начальное положение, начальная скорость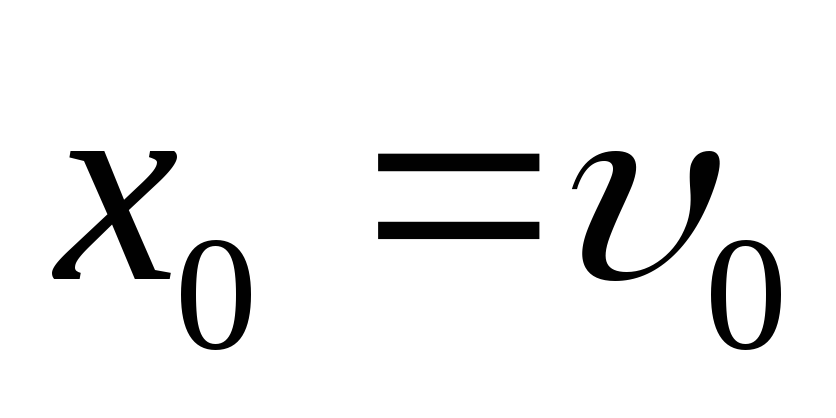. Найти закон (уравнение) движения точки по оси.

Дифференциальное уравнение движения точки в проекции на ось будет:или

(a)

Решим уравнение (а).

1.

уравнение (а) будет

Так как , то- это уравнение с разделяющимися переменными. Разделим переменные и проинтегрируем:

;

;

;

;

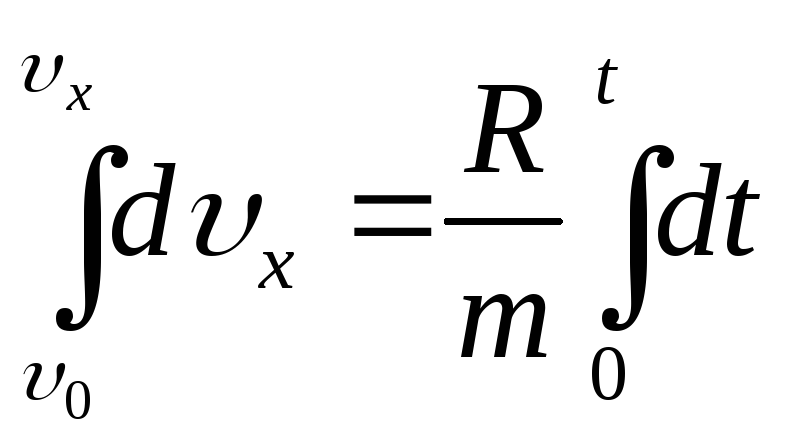Откуда

Так как , то

Разделим переменные и проинтегрируем:

;

;

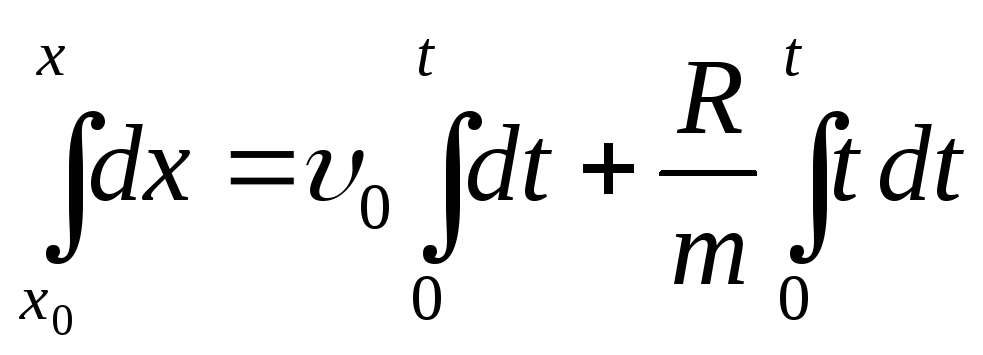окончательно: – закон движения точки М относительно оси.

2.

Уравнение (а) будет или

Разделим переменные и проинтегрируем:

;

;

;

где

.

Далее или

Разделим переменные и проинтегрируем:

;

;

;

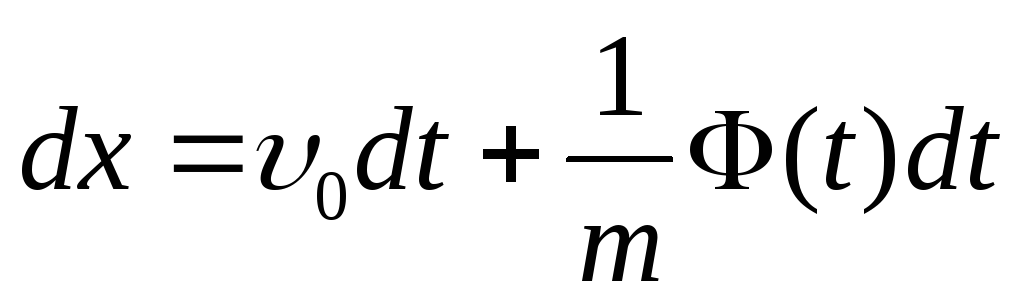– Закон движения

3.

Уравнение (а) будет или

Умножив обе части на, получим:

Так как , то, интегрируя, получим:;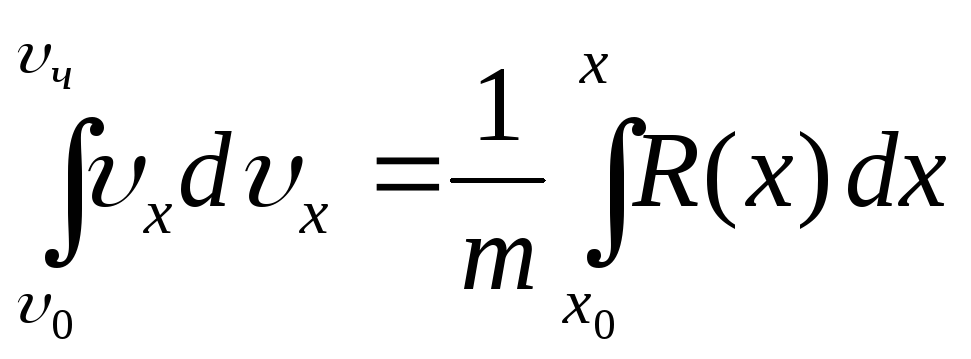

(б)

где

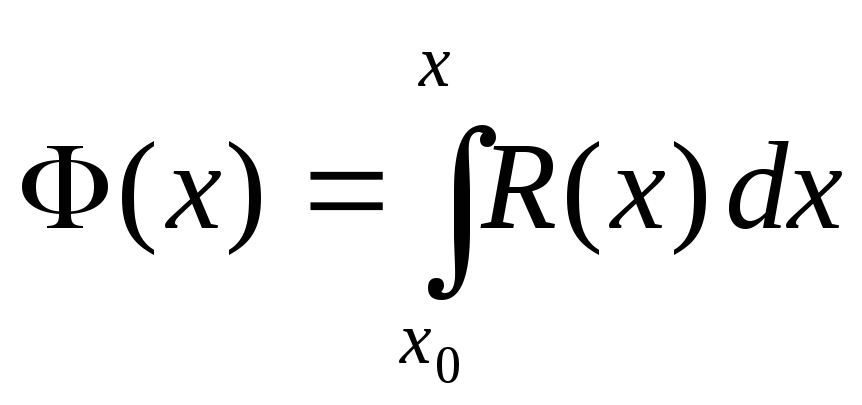
Из равенства (б), имеем , откуда

При дальнейшем решении знак перед корнем выбираем в зависимости от того, в каком направлении (положительном или отрицательном движется точка относительно оси x).

Далее

Разделим переменные и проинтегрируем:

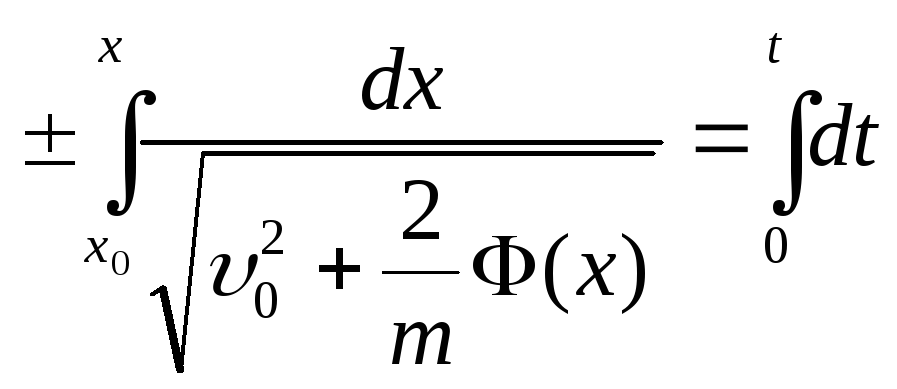
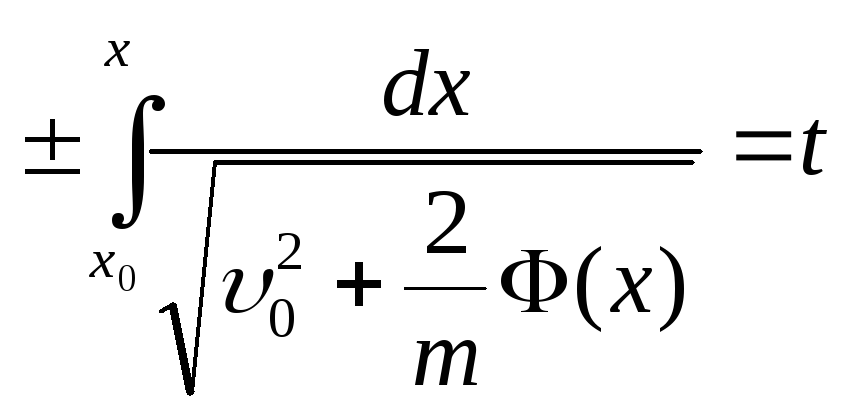
Замечание 1.

Если , где, то уравнение (а) будет, которое рекомендуется решать, как линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами

Замечание 2.

Если , гдеили, то уравнение (а) будет

, которое рекомендуется решать, как линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами

4.

Уравнение (а) будет: или

(в)

Первый способ решения.

Разделим переменные и проинтегрируем

;

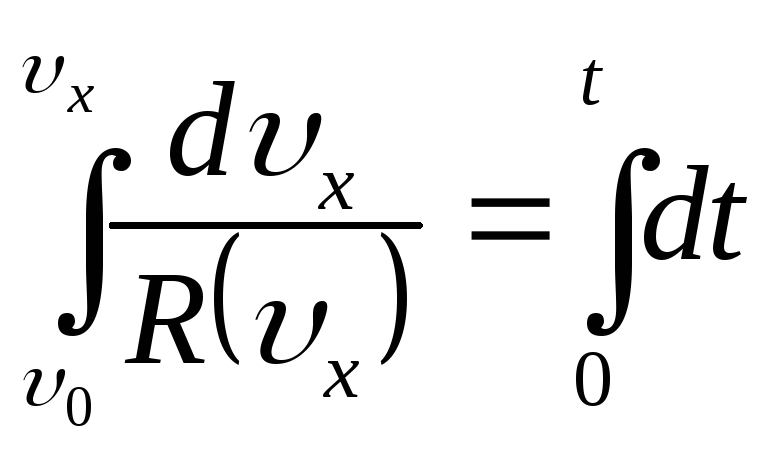(г)

где 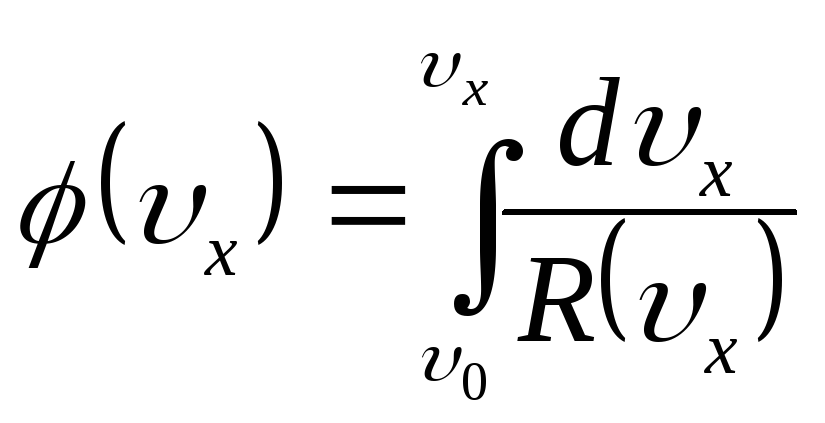. Из уравнения (г) находим.

Далее . Разделим переменные и проинтегрируем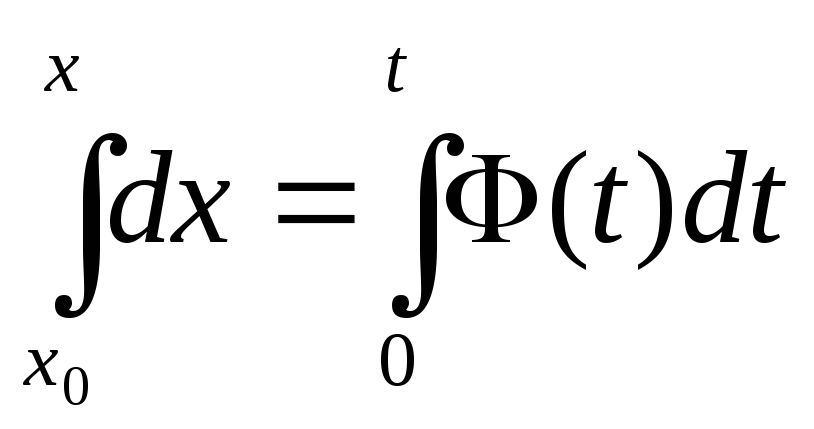

откуда

Второй способ решения.

Умножим обе части уравнения (в) на , получим

.

Разделим переменные и проинтегрируем: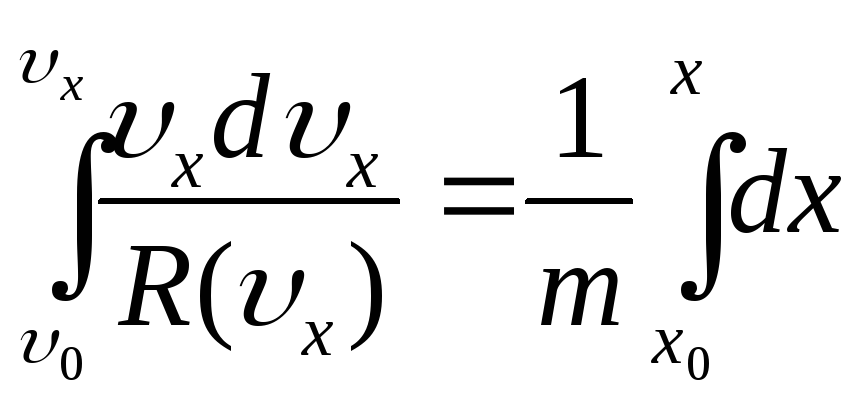

(д)

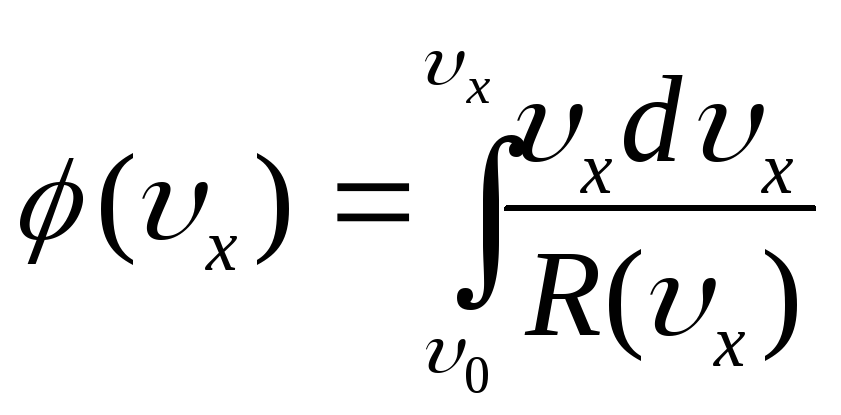. Из уравнения (д)или

Разделим переменные м проинтегрируем:

Замечание 3

Если , где, то уравнение (1) будет:, которое рекомендуется решать, как и в замечании 1.

Замечание 4

Если , где, или, то уравнениние (а) будет, которое рекомендуется решать, как и в замечании 2

Замечание 5

Если , то уравнение (а) будет,которое рекомендуется решать, как и в замечании 1

Замечание 6.

Если, где, или, то уравнение (а) будет, которое рекомендуется решать, как и в замечании 2.

16. Общие теоремы динамики точки

16.1 Количество движения и кинетическая энергия точки. Импульс силы.

16.2 Теорема об изменении количества движения точки.

16.3 Момент количества движения точки относительно центра и оси. Теорема об изменении количества движения точки (теорема моментов)

4. Работа силы. Мощность.

5. Примеры вычисления работы.

6. Теорема об изменении кинетической энергии точки.