15.2. Дифференциальные уравнения движения материальной точки в проекциях на оси естественного трехгранника.

Пусть точка М массы mдвижется по заданной гладкой кривой, лежащей в одной плоскости(рисунок 2).

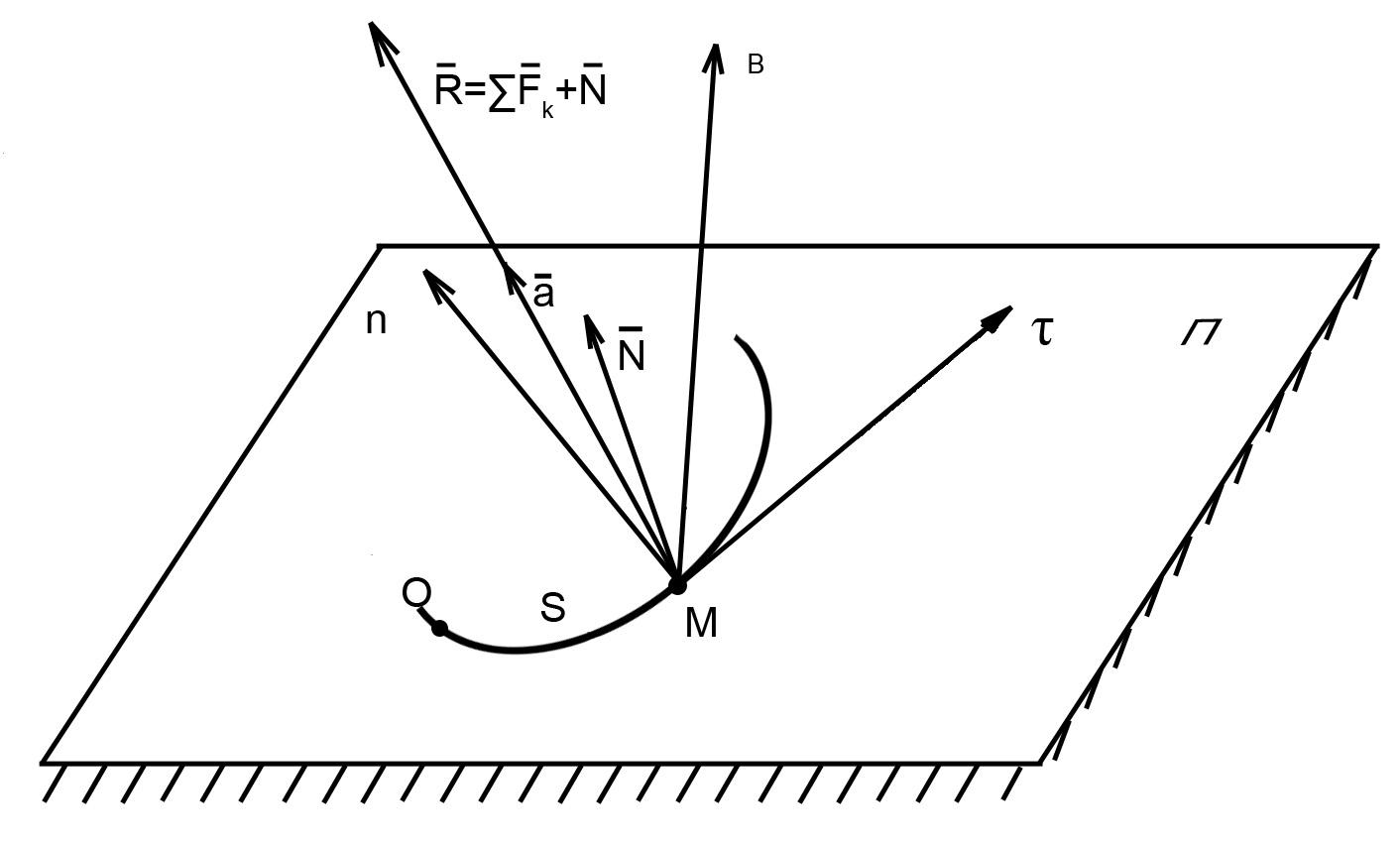
Рис. 2

Выберем на кривой начало отсчета 0, и будем определять положение точки М координатой . Поместим начало отсчета подвижных осей естественного трехгранникаMinв точкеM, где осьMiнаправлена по касательной к траектории в сторону положительного отсчета координатыS; осьMn– по нормам к траектории, лежащей в плоскости П и направленной в сторону вогнутости траектории: осьMb(b- бинормаль) – перпендикулярна к первым двум так, чтобы она образовала с ними первую систему осей.

По аксиоме связей из статики, данную точку сделаем свободной, заменив связь ее реакцией

Запишем для данной точки основное уравнение динамики

Проецируя это равенство на оси естественного трехгранника, учитывая, что вектор ускорения расположен в плоскости П, а, получим:

,,

Так как ,, то дифференциальные уравнения движения точки будут:

(2.3)

Если точка Mбудет свободной, тои дифференциальные уравнения движения будут:

(2.4)

15.3. Принцип Даламбера для материальной точки

Пусть точка М массы mдвижется прямолинейно под действием сили, и получает некоторое ускорение.

Запишем для данной точки основное уравнение динамики (1.2)

, где

Введем в рассмотрение величину , имеющую размерность силы. Эта сила, равная по модулю произведению массе точки на модуль ее ускорения и направленная противоположно ускорению называется силой инерции точки

Так как ,, тоили

(2.5)

Равенство (2.5) выражает принцип Даламбера для материальной точки: геометрическая сумма заданных сил, силы реакции и силы инерции точки равны нулю.

Если точка будет двигаться по некоторой криволинейной траектории, то

и сила инерции или, где,(рисунок 3).

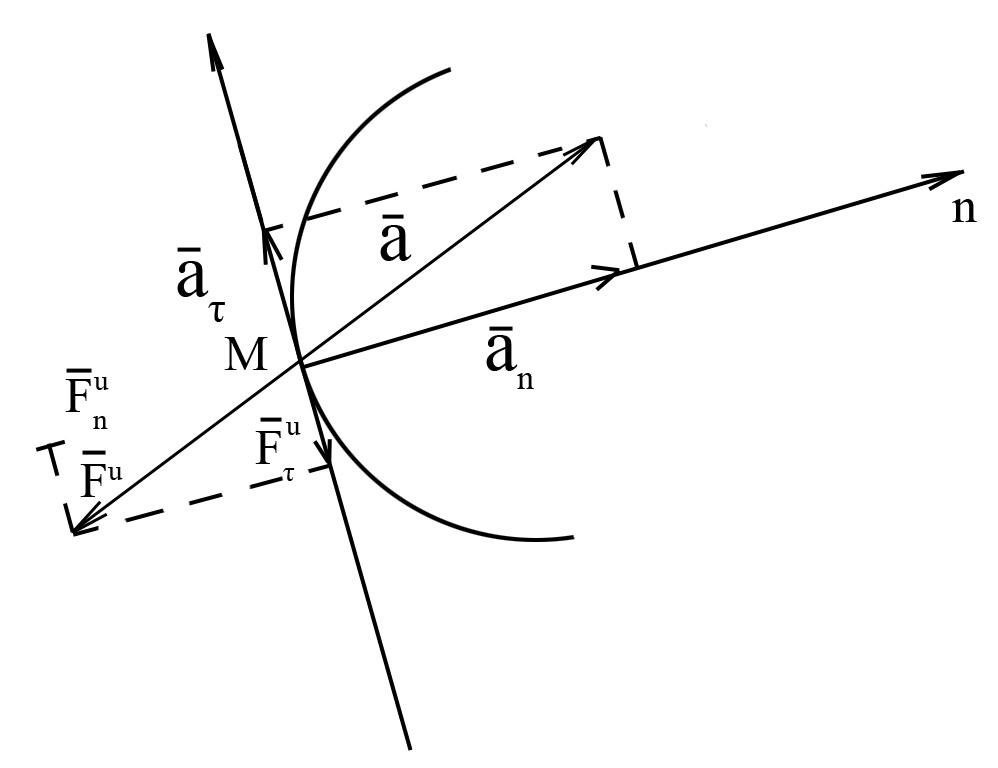
Рис. 3

По модулю ,.

В этом случае принцип Даламбера запишется в виде .

Так как все силы приложены к одной точке, то принцип Даламбера позволяет перейти от динамики точки к рассмотрению равновесия системы сходящихся сил статики.

15.4. Две основные задачи материально точки

Первая задача.

Зная массу точки и закон (уравнение) движения определить равнодействующую или одну из сил, действующих на точку сил. Эта задача решается составлением дифференциальных уравнений материальной точки ((2.1), (2.2), (2.3), (2.4)), или принципа Даламбера (2.5).

Вторая задача.

Зная массу точки, все действующие на нее силы, а также ее начальное положение и начальную скорость определить закон (уравнение) движения точки.

Эта задача решается составлением дифференциальных уравнений движения материальной точки ((2.1), (2.2), (2.3), (2.4)) и их интегрированием.

Пример 1. Точка массы m= 8 кг движется в плоскостиoxyсогласно уравнениямx= 0,05t³,y= 0,3t². Определить модуль равнодействующей сил, приложенных к точке, в момент времениt= 4с.

Решение. Составим дифференциальные уравнения точки в проекциях на оси xиy:

. ТогдаВ момент времени,находим

Ответ: .

Пример 2. Точка массы m = 22кг движется по окружности радиуса r = 10м по закону S = 0,3t². Определить модуль равнодействующей сил, действующих на точку, в момент времени t = 5c.

Решение. Составим дифференциальные уравнения движения точки в проекциях на и естественного трехгранника.

,.

У нас ;.

Так как , то;

Тогда

Ответ: R = 23,8н

Пример 3. Груз массы 0,2 кг поднимается посредством нити по закону S = 1,25t³. Найти натяжение нити в момент времени t = .

Решение.

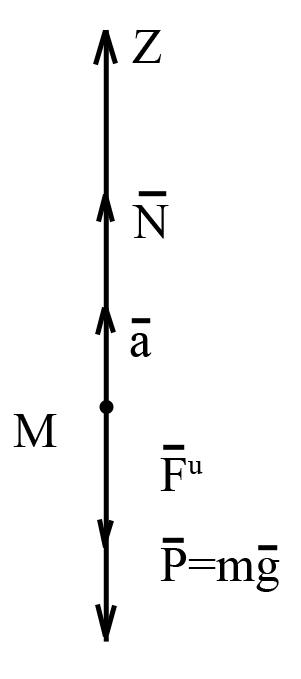
Рис. 4

Груз движется под действием силы тяжести и реакции. Для определения натяжения нитиN воспользуемся принципом Даламбера (рисунок 4.):

. Спроецируем это равенство на осьZ, получим , откуда. У нас. Тогда.

Ответ: 2,46н.