24. Теория удара

24.1 Исходные предположения и основной закон

В теории удара изучаются явления, связанные с воздействием на материальные объекты мгновенных бесконечно больших сил , действующих в продолжении бесконечно малых интервалов времени. Такие силы называют ударными. Под бесконечно большой и бесконечно малой величинами (силы и времени) понимаются такие величины, при которых результирующая величина:

, (11.1)

называемая ударным импульсом, остается величиной конечной.

Основными допущениями теории удара являются:

1. Действия неударных (конечных) сил за время удара ничтожно малы, а потому такие силы можно не учитывать.

2. Материальные точки в процессе удара не изменяют своего положения.

3. При ударе происходят лишь мгновенные ( конечные ) изменения скоростей точек системы.

Основное уравнение теории удара следует из теоремы об изменении количества движения материальной точки и записывается так:

, (11.2)

где - масса,- скорости в начале и конце удара,- ударный импульс. Закон (11.2) гласит: изменение количества движения материальной точки за время удара равно ударному импульсу. Если точка подвержена действию нескольких ударных сил, то в (11.2) справа будет стоять геометрическая сумма ударных импульсов отдельных сил.

Ускорения точек при ударе оказываются бесконечно большими и потому не рассматриваются. По этой причине задачи на удар сводятся к решению конечных (алгебраических или геометрических) уравнений, а не дифференциальных, к которым приводит второй закон Ньютона.

Заметим еще, что в результате действия ударных сил на несвободную систему материальных точек возникают ударные реакции связей.

А потому изменение скорости каждой точки системы определяется не только импульсом приложенной к ней ударной силы, но также и импульсами мгновенно развивающихся реакции связей. Эти последние не известны и определяются вместе с изменениями скоростей точек системы.

24.2 Упругий и неупругий удары. Коэффициент восстановления

Представим себе два абсолютно гладких шара, которые движутся поступательно, прямолинейно с разными скоростями (), и в некоторый момент времени происходит их столкновение (рис. 52)

Прямую линию ХХ, совпадающую с общей нормалью к поверхностям в точке соприкосновения, называют линией удара. Удар называют центральным если центры масс тел лежат на линии удара. И, наконец, центральный удар называют прямым, если скорости центров масс тел в начале удара направлены по линии удара. Именно таком случай предполагается на рис.

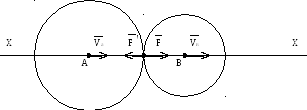
Рис. 52

Итак, пусть происходит соприкосновение шаров и наступает удар. Весь процесс удара занимает две фазы.

1. Фаза деформации. Тела деформируются, отрезок АВ сокращается. Фаза заканчивается в тот момент, когда скорости тел становятся равными. Ударный импульс за фазу деформации равен:

,

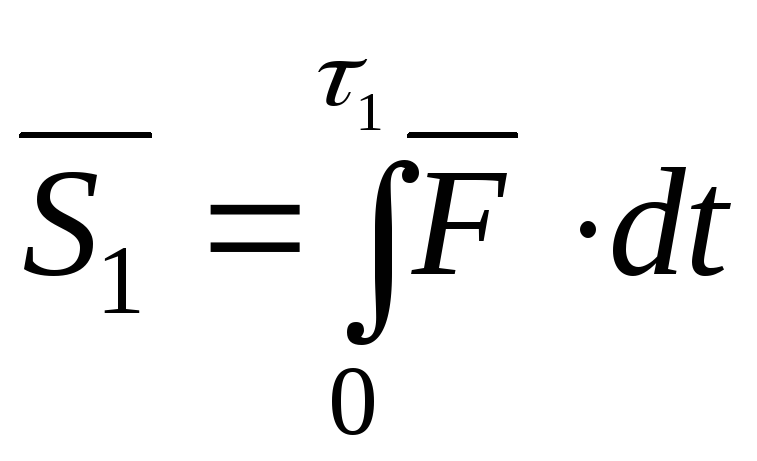где - продолжительность фазы деформации.

2. Фаза восстановления. Длина отрезка АВ увеличивается. Фаза заканчивается моментом отделения тел. Ударный импульс за эту фазу равен:

,

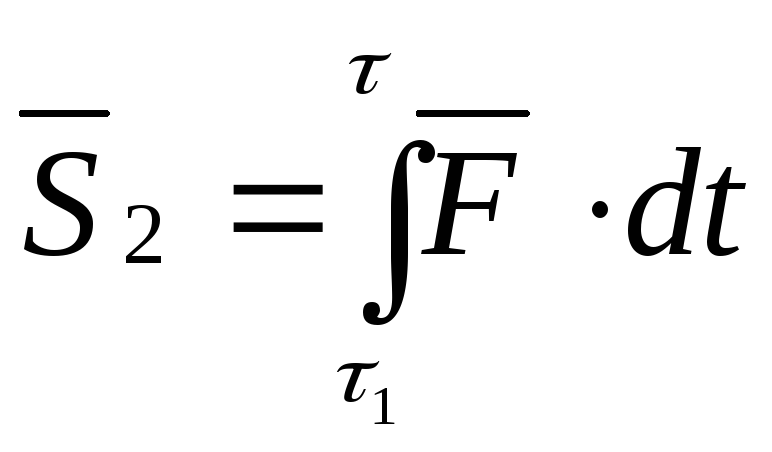Здесь: - время удара,- продолжительность фазы восстановления.

Для оценки характера удара вводится безразмерная величина

которую называют коэффициентом восстановления. Определяется данный коэффициент опытным путем. Его действительные численные значения заключены между 0 и 1. в теоретической механике рассматривают и предельные значения, а потому .

При k=0 импульс, т.е. фаза восстановления отсутствует. Такой удар называют абсолютно неупругим. Приk=1,. Это означает, что за фазу восстановления тела полностью восстанавливают свою форму. Такой удар называют абсолютно упругим.