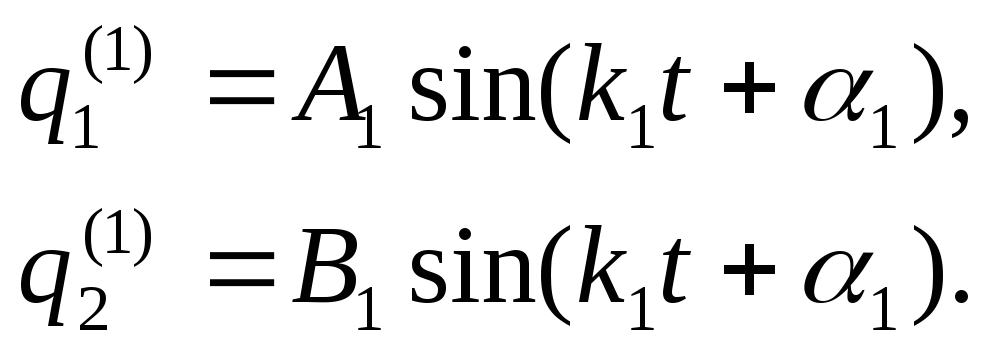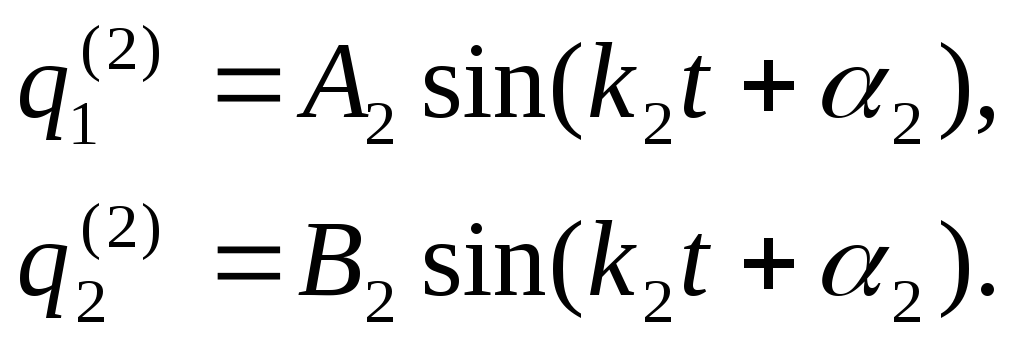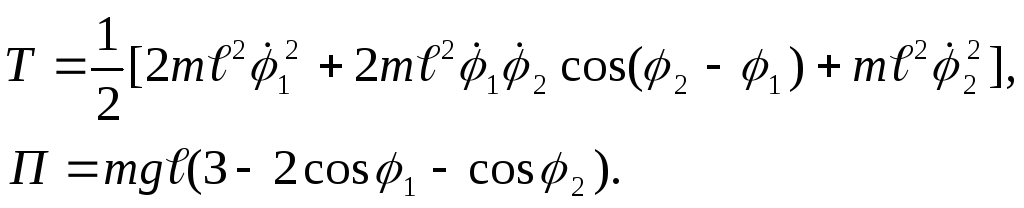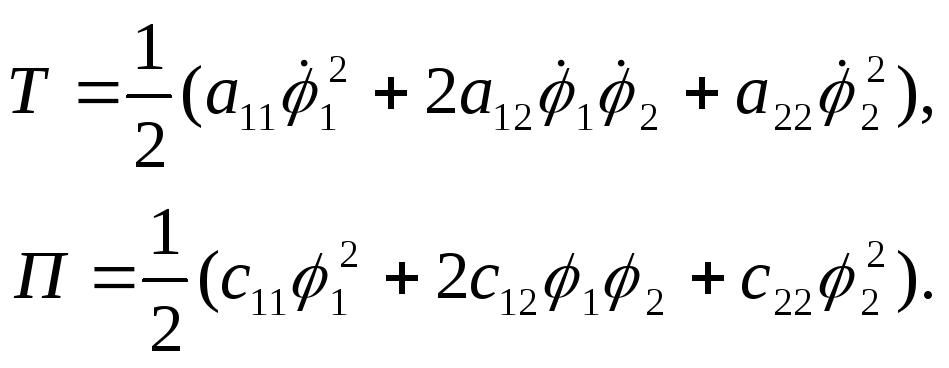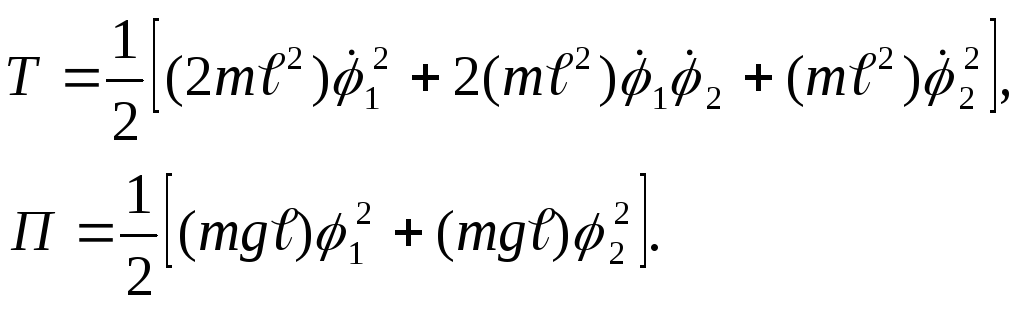23.3 Малые свободные колебания системы с одной степенью свободы

Для системы с одной степенью свободы уравнения Лагранжа при малых колебаниях:

Кинетическая и потенциальная энергия:

.

Выполняя над Т и П указанные действия, получим:

(10.5)

или

(10.6)

где - угловая частота колебаний,- период.

Общее решение уравнения (10.6) можно принять в одной из таких форм:

,

(10.7)

,

где - произвольные постоянные, определяемые по начальным условиям; А – амплитуда, α – начальная фаза. Приняв во внимание разложение функции, нетрудно установить связь между одной и другой парой постоянных:

.

(10.8)

Остановимся на первом представлении и найдем постоянные Aи α. Положим, что в начальный момент времениt= 0 задано:

(10.9)

Исходим из того, что

Сюда подставим t = 0и (10.9):

Решая данную систему, найдем:

(10.10)

Замечание. Если в задаче требуется определить лишь частоту или период малых колебаний, то нет необходимости в составлении и решении дифференциального уравнения колебаний. В этом случае достаточно составить кинетическую и потенциальную энергию в форме , и затем найти то, что требуется:

Пример.

Однородный цилиндр радиуса Rи массыMможет кататься без скольжения по горизонтальной плоскости. В точках и цилиндра шарнирно прикреплены пружины длинойи жесткостью каждая. Другие концы пружин закреплены на плоскости катания. Когда диаметрABгоризонтален (положение равновесия), пружины не напряжены. Определить период малых колебаний цилиндра.

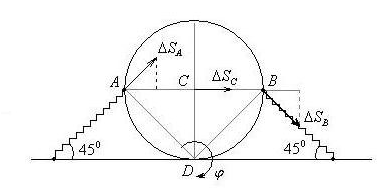
Рис. 49

Система имеет одну степень свободы. В качестве обобщенной координаты возьмем угол поворота цилиндра. ТочкаDявляется мгновенным центром скоростей. При малых колебаниях её можно считать неподвижной. В решении задачи ничего не изменится, если в точкеDввести неподвижный шарнир. Колебания можно считать малыми до тех пор, пока можно считать постоянными углы наклона пружин к плоскости.

Перемещения точек при малых колебаниях направлены по скоростям этих точек. Причем для малых перемещений также выполняется теорема о равенстве проекций. Например, в нашей задаче:

Итак, сообщим цилиндру бесконечно малый поворот вокруг точкиD. Производнаябудет угловой скоростью. Кинетическая энергия найдется по формуле:

где .

Потенциальная энергия вызывается силами упругости двух пружин. Перемещения точек AиB:

направлены по осям пружин; - удлинение,- осадка. Отсюда следует:

,

где .

Период малых колебаний равен:

23.4 Малые свободные колебания системы с двумя степенями свободы

Пусть дана система с двумя степенями свободы и - обобщенные координаты. Кинетическая и потенциальная энергия системы дается формулами (10.2):

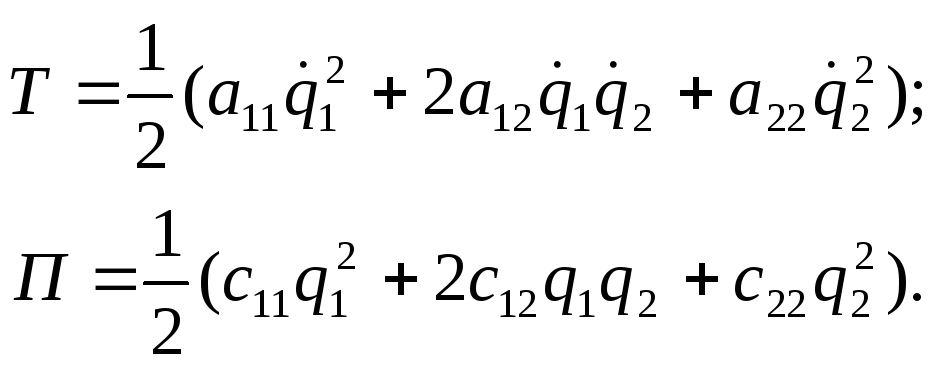
Функции Т и П определенно положительны, а потому:

(10.11)

Уравнения Лагранжа для соответствующих координат:

(10.12)

(9.46)

Подставив (10.2) в (10.12), получим дифференциальные уравнения малых колебаний системы с двумя степенями свободы:

(10.13)

Примем решение системы в виде:

,

(10.14)

где A,B,k,α– некоторые постоянные. Подставив (10.14) в (10.13), и сократив на, получим:

(10.15)

Система имеет нулевое решение A=B=0, соответствующее устойчивому положению равновесия. Для ненулевых решений составим из (10.15) отношение:

.

(10.16)

Из первого равенства находим:

.

(10.17)

Данное условие, служащее для определения частот, называют уравнением частот. Запишем его в виде:

(10.18)

где ;.

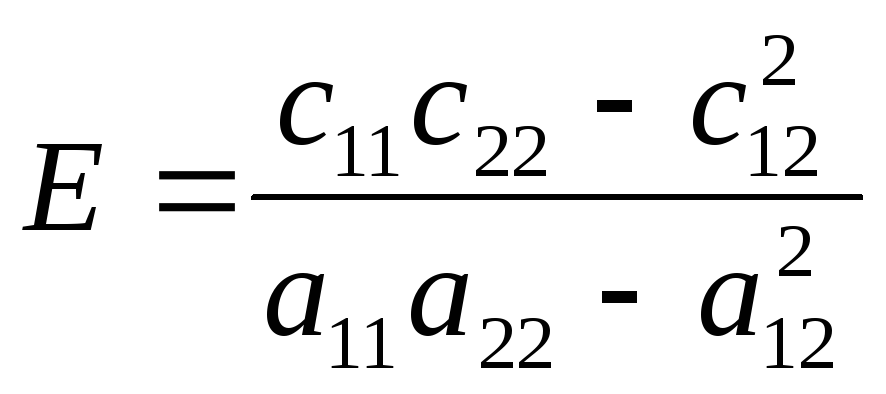Квадратное (относительно ) уравнение (10.18) в силу неравенств устойчивости имеет два вещественных положительных корня. Расположим их в порядке возрастания:

(10.19)

Отсюда найдем две частоты. Одна из них - низшая, другая- высшая. Это собственные частоты системы. Колебание с частотойназывают первым главным колебанием, с частотой- вторым главным колебанием системы.

Вернувшись к решению (10.14), мы можем теперь записать – для первого главного колебания:

(10.20)

Для второго главного колебания:

(10.21)

Главные колебания являются колебаниями гармоническими.

Подставив поочередно ив (10.16 ), найдем связи между амплитудамиAиBв главных колебаниях:. Множителииназывают коэффициентами собственных форм (коэффициентами распределения амплитуд). Они могут быть как положительными, так и отрицательными. Приобе координаты в главном колебании находятся в одной фазе; при- в противофазе.

Результирующее движение по каждой координате будет суммой двух главных колебаний:

(10.22)

где - зависят от начальных условий,- от начальных условий не зависят и определяются параметрами самой колебательной системы. В общем случае частотыинесоизмеримы, а потому результирующее движение не будет периодическим.

Примеры.

1. Определить собственные частоты и собственные формы колебаний (малых) двойного математического маятника, образованного двумя материальными точками равной массы mи двумя стержнями длинойкаждый.

Подобная система в общем виде была рассмотрена в примере 2 (§34). Воспользуемся полученными там формулами (2) и (3).

При , получим:

(1)

Функции Tи П должны быть приведены к квадратичным формам:

(2)

Так как колебания малые, то с точностью до малых второго порядка включительно:

(3)

С учетом (3) из (1), замечаем:

(4)

Сравнивая (4) и (2), замечаем:

Раскрывая уравнение (7.52) частот, получим:

Из (9.50) находим коэффициенты распределения: .

Первое главное колебание:

Движение в фазе - в каждое мгновение стержни вращаются в одном направлении.

Второе главное колебание:

Движение в противофазе – в каждое мгновение стержни вращаются в прямо противоположных направлениях.

Формы колебаний показаны на рис. 50. Во втором главном колебании имеется особенная точка F, которая остается неподвижной. Такие точки называют узлами. Концевая точкаOк узлам не относится.

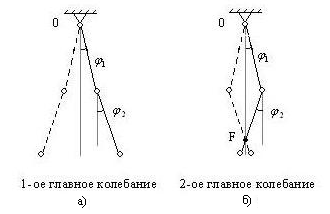
Рис. 50

2. Два твердых тела с массами ии две пружины, жесткостьюи, объединены в систему, которая располагается на гладкой горизонтальной плоскости и может совершать малые прямолинейные колебания.

Определить собственные частоты и установить формы колебаний.

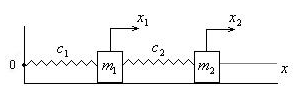
Рис. 51

Пусть - обобщенные координаты, отсчитываемые от положений равновесия тел. Кинетическая и потенциальная энергия:

Для упрощения выкладок возьмем упрощенный вариант: .

В результате:

.

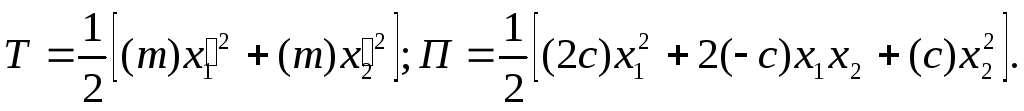Коэффициенты квадратичных форм:

Уравнение для вычисления частот:

Его решение:

По формулам ( 9.50) находим:

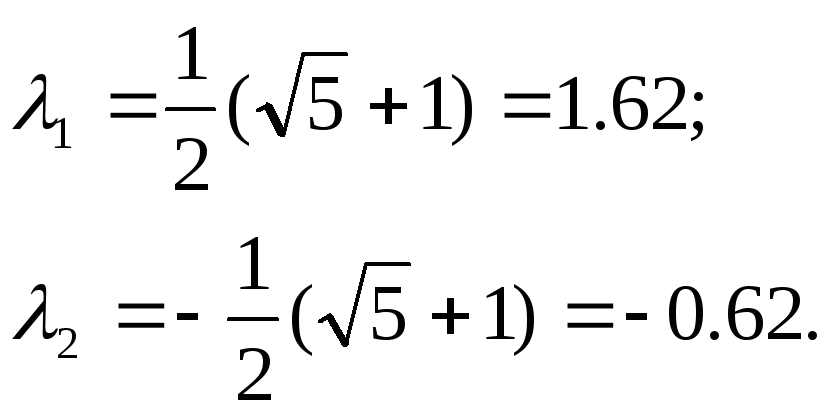
Картина движения показана на рис. 52. При втором главном колебании точка Fостается неподвижной (узел).

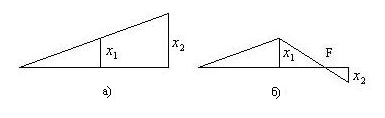
Рис. 52

Первое главное колебание:

Тела движутся в фазе, либо вправо либо влево. Амплитуда колебаний второго тела в 1,62 раза больше.

Второе главное колебание:

Тела движутся в противофазе: либо навстречу друг другу, к узлу, либо расходятся от узла. Амплитуда колебаний второго тела составляет 0,62 амплитуды первого.
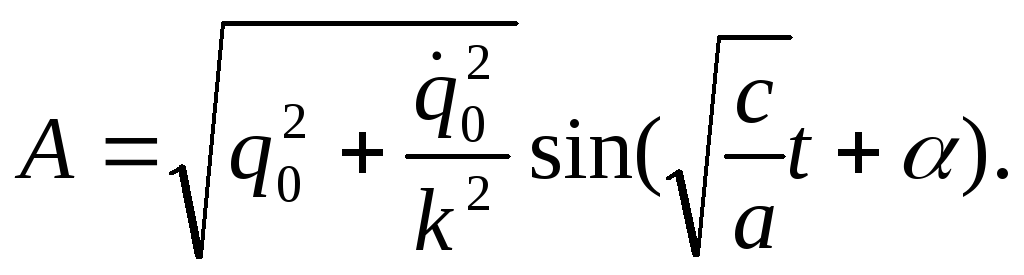
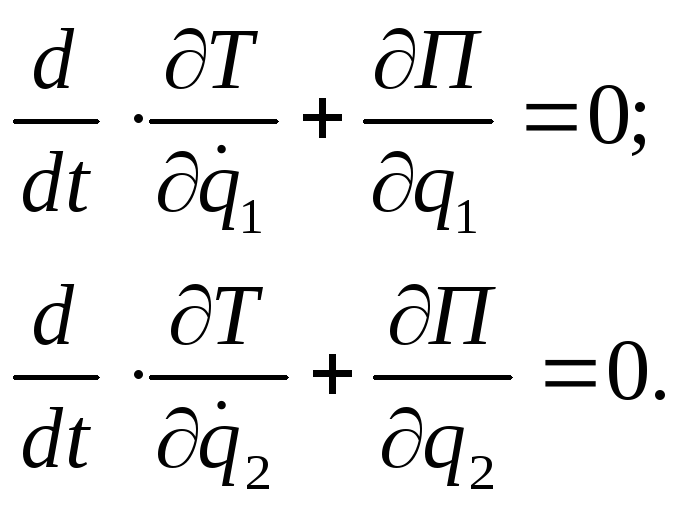
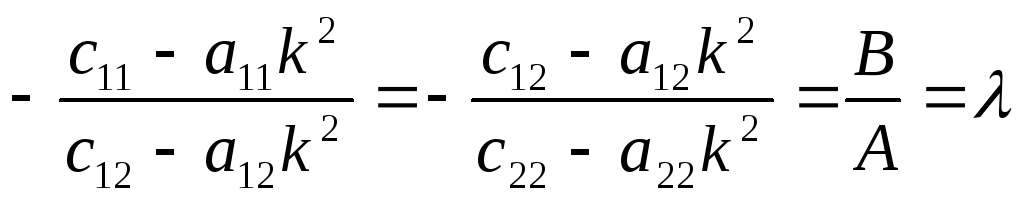