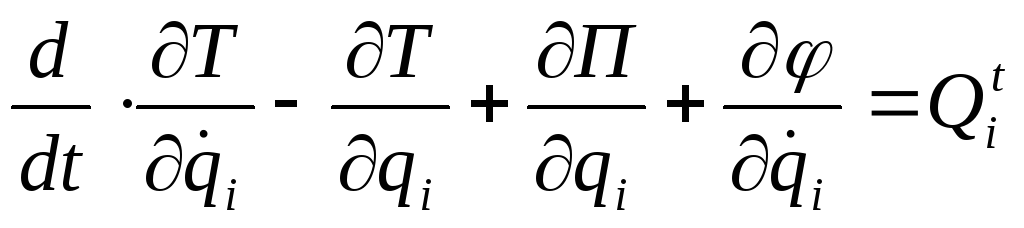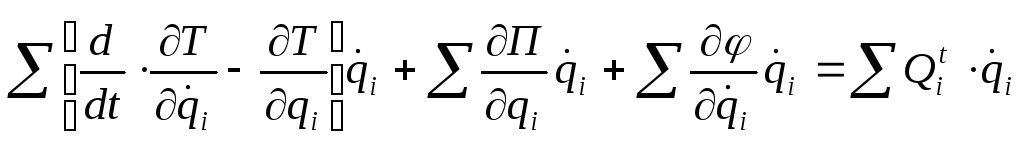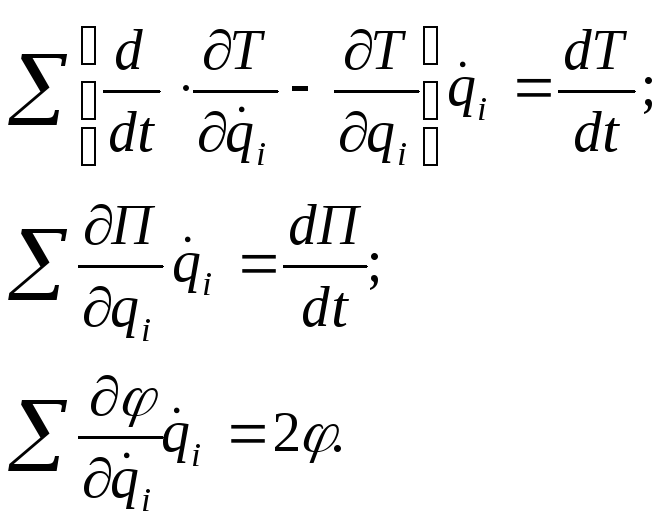- •Раздел 3. Динамика
- •Глава 14. Введение в динамику.
- •14.2 Законы механики Галилея – Ньютона.
- •15. Дифференциальные уравнения движения материальной точки. Принцип Даламбера для материальной точки. Две основные задачи динамики точки.
- •15.2. Дифференциальные уравнения движения материальной точки в проекциях на оси естественного трехгранника.
- •15.3. Принцип Даламбера для материальной точки
- •15.4. Две основные задачи материально точки
- •15.5. Интегрирование дифференциальных уравнений движения материальной точки
- •16. Общие теоремы динамики точки
- •16.1. Количество движения и кинетическая энергия точки. Импульс силы.
- •16.2. Теорема об изменении количества движения точки.
- •16.3. Момент количества движения точки относительно центра и оси. Теорема об изменении момента количества движения точки (теорема моментов)
- •16.4. Работа силы. Мощность
- •16.5. Примеры вычисления работы.
- •16.6. Теорема об изменении кинетической энергии точки
- •17. Свободные прямолинейные колебания материальной точки
- •17.1. Свободные горизонтальные колебания точки
- •17.2. Свободные вертикальные колебания груза
- •18. Относительное движение материальной точки
- •18.1. Дифференциальные уравнения движения материальной точки в неинерциальной системе отсчета.
- •18.2. Частные случаи относительно движения точки
- •19. Момент инерции.
- •19.1. Момент инерции твердого тела. Радиус инерции.
- •19.2. Момент инерции твердого тела относительно параллельных осей (теорема Гюйгенса)
- •19.3. Момент инерции простейших твердых тел и плоских фигур
- •19.4. Центробежные моменты инерции. Понятие о главных осях инерции тела
- •20. Общие теоремы динамики системы
- •20.1 Вводные определения и дифференциальные уравнения движения
- •20.2 Теоремы об изменении количества движения и теорема о движении центра масс
- •20.3 Теорема об изменении кинетического момента
- •20.4 Теорема об изменении кинетической энергии
- •21. Приложение теорем динамики системы к динамике твердого тела
- •21.1. Дифференциальные уравнения поступательного движения твердого тела
- •21.2. Определение динамических реакций подшипников при вращении твердого тела вокруг неподвижной оси
- •21.3 Дифференциальные уравнения плоскопараллельного (плоского) движения твердого тела
- •21.4 Элементарная теория гироскопа
- •21.5 Дифференциальные уравнения движения твердого тела вокруг неподвижной точки (сферического движения)
- •22. Начала аналитической механики
- •22.1 Введение
- •22.2 Принцип возможных перемещений
- •22.3 Принцип Даламбера. Общее уравнение динамики
- •22.4 Уравнения Лагранжа второго рода
- •22.5 Принцип Гамильтона – Остроградского
- •22.6 Обобщенное уравнение энергии
- •23. Малые колебания консервативной системы около положения равновесия
- •23.1 Кинетическая и потенциальная энергия малых колебаний
- •23.2 Понятие об устойчивости равновесия
- •23.3 Малые свободные колебания системы с одной степенью свободы
- •23.4 Малые свободные колебания системы с двумя степенями свободы
- •24. Теория удара
- •24.1 Исходные предположения и основной закон
- •24.2 Упругий и неупругий удары. Коэффициент восстановления
- •24.3 Общие теоремы при ударе
22.5 Принцип Гамильтона – Остроградского
Данный принцип касается в первую очередь, скажем так, философии механического движения. Сущность вопроса состоит в следующем. Представим себе движущуюся механическую систему. Поставим ей в соответствие наглядный геометрический образ – некоторую условную точку, которую назовем изображающей точкой. Это позволяет ввести понятие о траектории изображающей точки (рис. 45). Возьмем на траектории положения A0иA1, соответствующие моментам времениt0иt1. При заданных силах и характере связей можно представить множество путей перехода системы изA0вA1за времяt1- t0. Спрашивается, какой путь выбирает система? Или иначе, какой путь является истинным? Принцип Гамильтона – Остроградского дает ответ на этот вопрос.
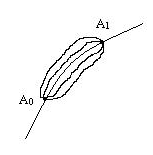
Рис. 45
Вернемся к общему уравнению динамики:
|
|
(9.33) |
Отделим работы сил активных от работы сил инерции и проинтегрируем равенство по времени в пределах от t0доt1:
|
|
(9.34) |
Допустим, что система движется в потенциальном силовом поле. В этом случае элементарная работа сил выражается особенно просто:
![]()
Доказывается также, что
![]() .
.
Таким образом, равенство (9.34) приводится к виду:
|
|
(9.35) |
где L=T– П – кинетический потенциал.
Интеграл
![]() называют действием по Гамильтону.
называют действием по Гамильтону.
Окончательно, принцип Гамильтона – Остроградского:
|
|
(9.36) |
Принцип утверждает: действие по Гамильтону Sимеет стационарное значение на истинном пути системы, если к сравнению с ним привлекается многообразие окольных путей, совпадающих с истинным в начальный и конечный моменты времениt0иt1.
Если интервал времени t1- t0достаточно мал, действиеSимеет минимум. [Четаев].
22.6 Обобщенное уравнение энергии
Вернемся к уравнениям Лагранжа:
|
|
(9.37) |
Обобщенную силу представим в виде суммы трех слагаемых
|
|
(9.38) |
Здесь
![]() - потенциальная сила,
- потенциальная сила,
![]() - сила сопротивления,
- сила сопротивления,![]() - функция рассеяния,
- функция рассеяния,
![]() - возмущающая сила, явно зависящая от
времени.
- возмущающая сила, явно зависящая от
времени.
Уравнения (9.37) примут вид:
|
|
(9.39) |
Умножим обе части в (9.39) на
![]() и сложим почленно:
и сложим почленно:
|
|
(9.40) |
Будем предполагать, что функции Tи![]() являются квадратичными формами
относительно обобщенных скоростей, П
зависит только от обобщенных координат.
При таких оговорках:
являются квадратичными формами
относительно обобщенных скоростей, П
зависит только от обобщенных координат.
При таких оговорках:
|
|
(9.41) |
Что касается правой части
![]() - она представляет собой мощность
возмущающих сил.
- она представляет собой мощность
возмущающих сил.
Уравнение (9.40) в окончательном виде:
|
|
(9.42) |
Его называют обобщенным уравнением энергии.
Отметим частные случаи.
При N = 0,
 = 0:
= 0:
![]() .
.
Если в системе нет возмущающих сил и сил сопротивления, полная энергия системы не изменяется (закон сохранения механической энергии).
При
 = 0:
= 0:
![]()
Если в системе нет сил сопротивления, энергия системы увеличивается, и скорость её нарастания равна мощности возмущающих сил.
Характерно для фазы разгона систем без сопротивления.
При N= 0:
![]()
Если в системе нет возмущающих сил, энергия системы убывает, и скорость её убывания равна удвоенной функции рассеяния.
Характерно для затухающих процессов.
При
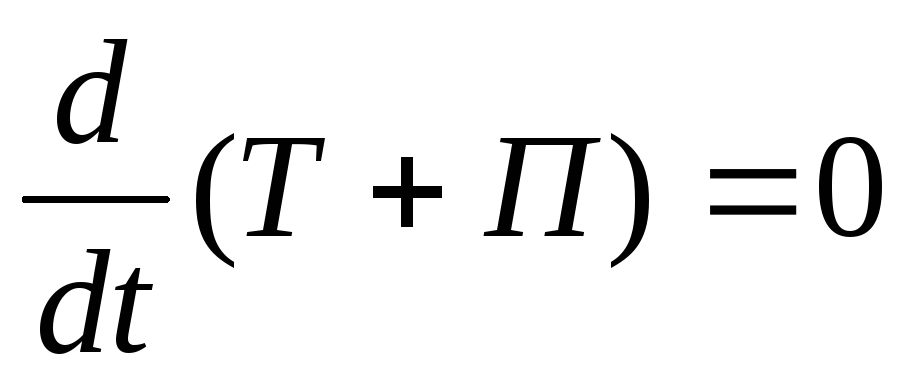 :
:
![]() .
.
В системах с сопротивлением, при постоянстве механической энергии, мощность возмущающих сил равна удвоенной функции рассеяния. Характерно для установившихся процессов.

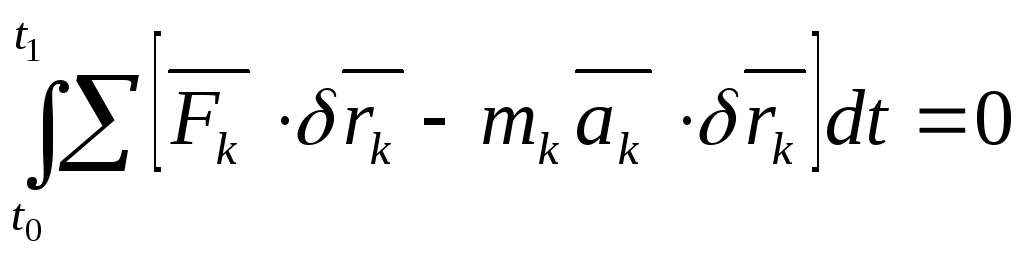 .
.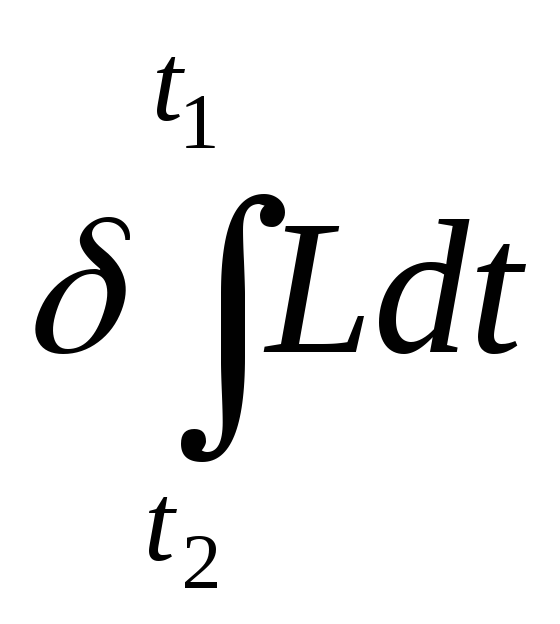 ,
,