22.4 Уравнения Лагранжа второго рода

Уравнения Лагранжа второго рода предназначены для составления дифференциальных уравнений движения голономных систем довольно общего вида. Если кинетическая и потенциальная энергии системы определены и выражены через обобщенные координаты, то последующие выкладки в уравнениях Лагранжа доведены до автоматизма. Важное достоинство получаемых таким образом уравнений – они не содержат реакций связей (к тому же неизвестных). Но если возникает необходимость определения таких реакций, то метод Лагранжа (путем введения так называемых избыточных координат) позволяет решать и эту задачу.

Будем исходить из общего уравнения динамики:

(9.21)

Возьмем систему с идеальными стационарными связями (уравнения Лагранжа не меняют своей формы и при нестационарных связях), и пусть - обобщенные координаты системы. Тогда радиус – вектор каждой точки может быть выражен через обобщенные координаты:

(9.22)

Отсюда находим формулы для вычисления скорости:

(9.23)

и возможного перемещения:

(9.24)

Нетрудно убедиться в таких тождествах:

(9.25)

Подставляя (9.24) в (9.21), получим:

(9.26)

Здесь - обобщенная сила (как уже известно, из аналитической статики), соответствующая обобщенной координате.

С помощью (9.25) доказывается, что:

,

где Т – кинетическая энергия системы.

В результате уравнение (9.21) принимает вид:

(9.27)

Это уравнение называют общим уравнением динамики в обобщенных координатах. Все вариации в данном уравнении независимы, их можно сообщать поочередно, а потому, как нетрудно видеть, выражения в скобках будут нулями.

Мы приходим, таким образом, к уравнениям Лагранжа второго рода:

(9.28)

При движении системы в потенциальном силовом поле обобщенные силы выражаются через потенциальную энергию, и уравнения (9.28) принимают вид:

(9.29)

В этом случае их можно представить также в такой компактной форме:

(9.30)

где L=T-M– функция Лагранжа (кинетический потенциал).

Замечание. Обобщенную координату называют циклической, если она не входит явно в функцию LЛагранжа. Нециклические координаты называют позиционными.

Пусть – циклическая координата. Для циклических координат уравнения (9.30) принимают вид:

(9.31)

Отсюда следует:

(9.32)

Данные интегралы называют циклическими. Они представляют собой обобщение законов сохранения количества движения и кинетического момента системы.

Примеры.

1. Механическая система состоит из малой и большой призм с массами mиM. Малая скользит по боковой грани большой призмы, которая, в свою очередь, движется по гладкой горизонтальной плоскости под действием заданной силы. Составить дифференциальные уравнения движения системы. Угол α наклона грани задан.

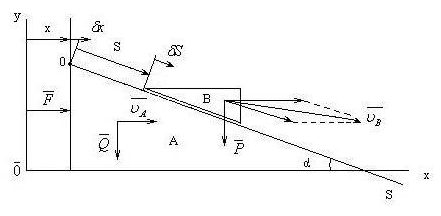
рис. 43.

Применим уравнения Лагранжа в форме (9.28). Рассматриваемая система имеет две степени свободы. За обобщенные координаты примем: х – абсолютное перемещение призмы А; S– относительное перемещение призмы В. Следует раскрыть уравнения:

(1)

Замечая, что кинетическая энергия не зависит от координат, а, следовательно,

,

находим левые части уравнений (1):

(2)

Обобщенные силы найдем из выражения элементарной работы, сообщая поочередно элементарные перемещения и. Остановим мысленно призмуBна грани призмыAи сообщим всей системе (как твердому телу) перемещение. Получим выражение для элементарной работы. Отсюда следует. Далее, при остановленной призме А сообщим перемещениемалой призме. Получим. Отсюда следует.

Подставляя (2) и выражения для обобщенных сил в (1), получим дифференциальные уравнения движения системы:

2. Составить дифференциальные уравнения колебаний двойного математического маятника. Маятник состоит из двух материальных точек M₁иM₂весаи, прикрепленных к концам двух невесомых стержней. Первый стержень может вращаться вокруг неподвижной горизонтальной осиO, а второй – вокруг оси, связанной с точкойM₁.

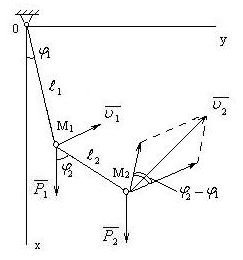
рис. 44.

Система имеет две степени свободы. За обобщенные координаты примем углы иотклонения стержней от вертикали. Для решения задачи воспользуемся уравнениями Лагранжа в форме (9.29). В нашем случае они запишутся так:

(1)

Кинетическая энергия системы равна:

(2)

При составлении выражения потенциальной энергии сил тяжести иногда возникает вопрос о том, в какой точке, на каком уровне принять нулевое значение П. От этого зависит внешняя форма выражения. Но здесь играет роль не П, а . Производная же во всех случаях будет одной и той же.

В рассматриваемой задаче представляется естественным принять П=0 для каждой точки, когда они находятся на оси Ох ( в положении равновесия). Если из отклоненного положения возвращать систему на ось Ох, работа сил тяжести будет величиной положительной. А потому:

(3)

Далее вопрос сводится к вычислению производных. Остановимся на координате . Имеем:

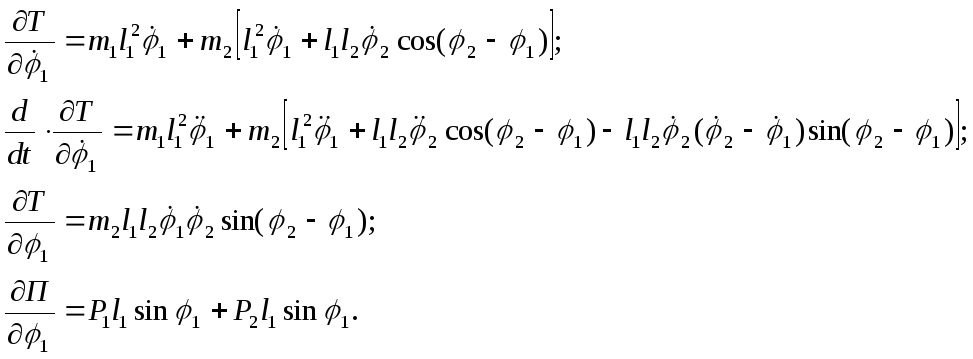
Совершенно аналогично – для координаты .

Окончательную систему запишем в виде: