22.3 Принцип Даламбера. Общее уравнение динамики

Пусть задана несвободная система материальных точек с идеальными, голономными, удерживающими связями. Освободим систему от связей и запишем основной закон динамики для каждой точки:

(9.15)

где - масса и ускорение точки (в инерциальной системе отсчета),- равнодействующая внешних сил,- равнодействующая внутренних сил. Представим (9.15) так, как мы это делали в геометрической статике, т.е. в виде условий равновесия:

.

(9.16)

Слагаемое (произведение массы на ускорение, взятое со знаком минус) называют силой инерции точки. Знак минус свидетельствует о том, что силы инерции направлены против ускорений. Названий сил инерции столько, сколько ускорений – касательная сила инерции, нормальная сила инерции и т.д.

Система Nравенств (9.16) выражает собой принцип Даламбера: в любое мгновение совокупность сил внешних, внутренних и сил инерции представляют собой уравновешенную систему сил. Если сами силы, входящие в (9.16) и их векторные моменты относительно некоторого центра О просуммировать по всем точкам системы, то получим:

(9.17)

где - главный вектор и главный момент сил инерции,- кинетический момент. Условия (9.17) прочитываются так: в каждое мгновение главный вектор и главный момент внешних сил уравновешиваются соответственно главным вектором и главным моментом сил инерции.

Теперь мы разделим все силы, приложенные к материальным точкам системы, по другому признаку: на активные и реакции идеальных связей, иначе говоря, на те, возможная работа которых не равна нулю, и на те, для которых та же работа равна нулю.

Вместо (9.16) будем иметь:

(9.18)

где - равнодействующая активных сил,- равнодействующая реакций идеальных связей. Принцип Даламбера в виде системы (7.18) трактуется так: в каждое мгновение совокупность сил активных, реакций идеальных связей и сил инерции представляет собой уравновешенную систему сил.

Вычислим сумму элементарных работ всех сил, входящих в (7.18). Приняв во внимание идеальность связей, придем к такому уравнению:

(9.19)

Его называют общим уравнением динамики. Общее уравнение динамики объединяет собой принцип Даламбера и принцип возможных перемещений. Оно утверждает: всякая система материальных точек с идеальными и удерживающими связями движется с таким образом, что возможная работа сил активных и сил инерции на любом возможном перемещении системы равна нулю.

В скалярной форме общее уравнение динамики имеет вид:

(9.20)

Примеры.

1. Два груза, один из которых опускается, а другой скользит без трения по крышке стола, связаны гибкой нерастяжимой нитью, перекинутой через блок. Стол установлен на шероховатом полу. Определить давление системы на пол.

Дано: m₁,m₂,m₃– массы грузов и стола. Массой блока и нити пренебречь.

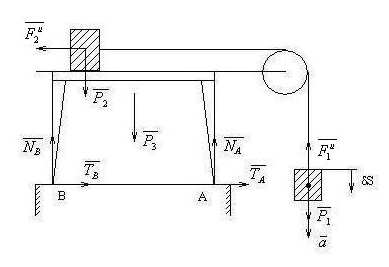
Найдем предварительное ускорение грузов. Следуя принципу Даламбера, приведем грузы в состояние покоя, приложив к ним силы инерции; сила инерции, так как стол неподвижен. Затем сообщим системе грузов элементарное перемещениеи запишем общее уравнение динамики:

Отсюда находим ускорение:

(1)

Для определения реакции пола воспользуемся принципом освобождаемости. Освободив систему от связей (отбросив пол) и введя реакции, сообщим системе возможные перемещения ии запишем общее уравнение динамики:

(2)

где . Из (2), посколькуинезависимы, получим:

Отсюда, с учетом (1), найдем реакции:

Реакции приложены к ножкам стола, давления – к полу. Очевидно, когда грузы находятся в движении, ножки стола меньше давят на пол. Тяжесть опускающегося груза частично теряется.

2. Чтобы переместить рельс на другое место, его положили на две трубы и подействовали силой . При заданной силе, массахMиm(рельса и трубы) определить ускорение рельса. Проскальзыванием между рельсом и трубами, между трубами и опорной плоскостью пренебречь.

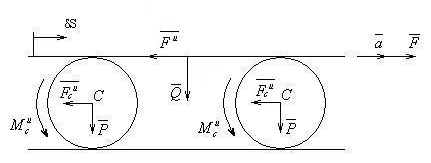
Рис. 42

Для решения задачи воспользуемся общим уравнением динамики. Пусть - искомое ускорение. Ускорениецентра трубы и её угловое ускорениеравны:

где R– радиус трубы.

Рельс движется поступательно, прямолинейно, а потому его силы инерции приводятся к равнодействующей , приложенной в центре масс. Труба находится в плоском движении. Её силы инерции, будучи приведенными к центру масс, дадут главный вектор и главный момент:

Уравновесив систему задаваемых сил силами инерции, сообщим рельсу элементарное перемещение . Для трубы. Остается записать общее уравнение динамики:

Отсюда, с учетом сказанного выше, найдем:

.