22.2 Принцип возможных перемещений

Условия равновесия системы в обобщенных силах.

Обратимся к системе материальных точек. Пусть ,, …,- активные силы, действующие на систему. Принцип возможных перемещений утверждает: для того, чтобы система, подчиненная идеальным, голономным, стационарным и удерживающим связям, находилась (оставалась) в равновесии, необходимо и достаточно, чтобы сумма возможных работ её активных сил на любом возможном перемещении системы, равнялась нулю, т. е. чтобы выполнялось равенство:

(9.8)

Докажем необходимость, т. е. когда есть равновесие, то непременно выполняется (9.8). При равновесии:

(9.9)

где - реакции идеальных связей. Если мы умножим обе части равенства (9.9) скалярно на, и затем просуммируем по всем точкам системы, то придем к (9.8).

Докажем достаточность, т. е. когда есть (9.8), то непременно будет и равновесие. Пусть (9.8) есть, а равновесия нет, и

(9.10)

Если мы обе части неравенства (9.10) умножим скалярно на и просуммируем по всем точкам системы, то придем к неравенству, которое не совместимо с (9.8), и значит, движение невозможно.

Чтобы равенство (9.8) было приспособленным для решения конкретных задач, его следует записать или в форме:

(9.11)

но лучше перейти к обобщенным координатам.

Пусть q₁,q₂, …,q_n– обобщенные координаты. Когда они введены, радиус-векторкаждой точки может быть представлен в виде:

Отсюда выражается возможное перемещение точки:

(9.12)

Подставив (9.12) в (9.8), придем к равенству

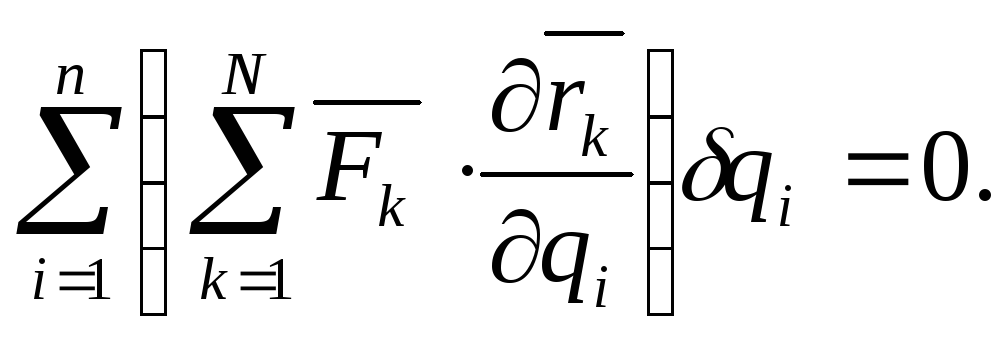
Сумму , называют обобщенной силой, отнесенной к координате. Обобщенные координаты выражаются через силы активные и зависят, кроме того, от геометрии системы. Если обобщенная координатаесть некоторое линейное перемещение точки,Q_iимеет размерность силы. Еслиесть угол поворота некоторого тела,Q_iимеет размерность момента силы. В результате (9.12) принимает вид:

(9.13)

Так как вариации независимы и их можно сообщать поочередно, то равенство (9.13) распадается на систему:

(9.14)

Таковы условия равновесия механической системы в обобщенных силах. Для равновесия системы с идеальными, голономными, удерживающими, стационарными связями необходимо и достаточно, чтобы обобщенные силы, соответствующие всем обобщенным координатам, были равны нулю.

При действии на систему потенциальных сил условия равновесия принимают особенно простую форму. В этом случае:

Здесь правая часть есть не что иное, как взятая со знаком минус производная от потенциальной энергии П по обобщенной координате . В результате условия равновесия запишутся так:

Примеры.

1. Однородный стержень длины 2lи веса Р вставлен без трения в качающуюся муфту. Помимо силы тяжести к стержню приложена, действующая по горизонтали, силаQ. Спрашивается, при каком смещенииSи угле наклона φ стержня к вертикали, возможно, его равновесие?

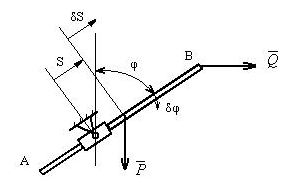
рис. 39

Система имеет две степени свободы. Составим уравнение элементарных работ, сообщая поочередно и. Получим:

Коэффициенты при вариациях являются обобщенными силами, которые при равновесии равны нулю. В результате приходим к системе:

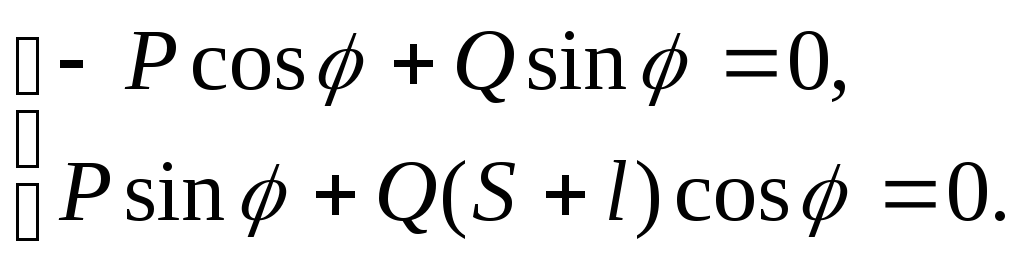
Отсюда находим:

При равновесии центр тяжести стержня должен находиться ниже оси вращения муфты.

2. Конструкция состоит из двух брусков, сочлененных шарниром С. Крепление в точках А и В видно непосредственно из рисунка. Определить момент в жесткой заделке.

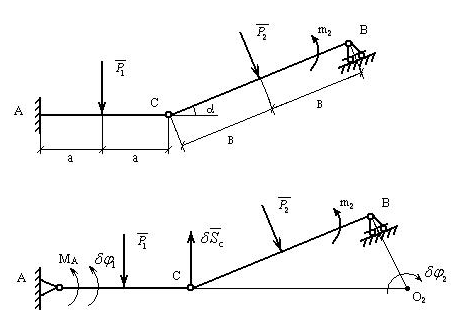
рис. 40

Заменим жесткое крепление в точке А неподвижным шарниром, введя искомый момент М_А. В результате получим систему с одной степенью свободы. Сообщим левой части элементарный поворот. Правая часть соответственно повернется на уголвокруг центра О₂. В плоских задачах центры поворота при малых перемещениях совпадают с мгновенными центрами скоростей.

Составим уравнение равновесия системы (сумма элементарных работ равна нулю), представляя работы как произведение момента силы (или пары сил) на угол поворота (для левой части моменты берутся вокруг точки А, для правой – вокруг точки О₂).

(1)

Правило знаков: если направление момента совпадает с направлением поворота, работа записывается со знаком плюс, в противном случае – со знаком минус.

Остается записать уравнение связи между и:

(2)

Решая (1) и (2) совместно, найдем: