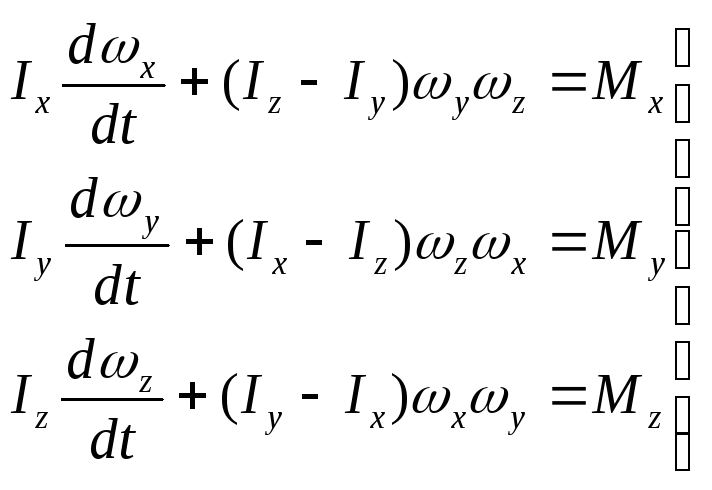21.5 Дифференциальные уравнения движения твердого тела вокруг неподвижной точки (сферического движения)

Пусть на твердое тело, имеющее неподвижную точку , действуют заданные внешние силыи реакциясвязи (рис. 37).

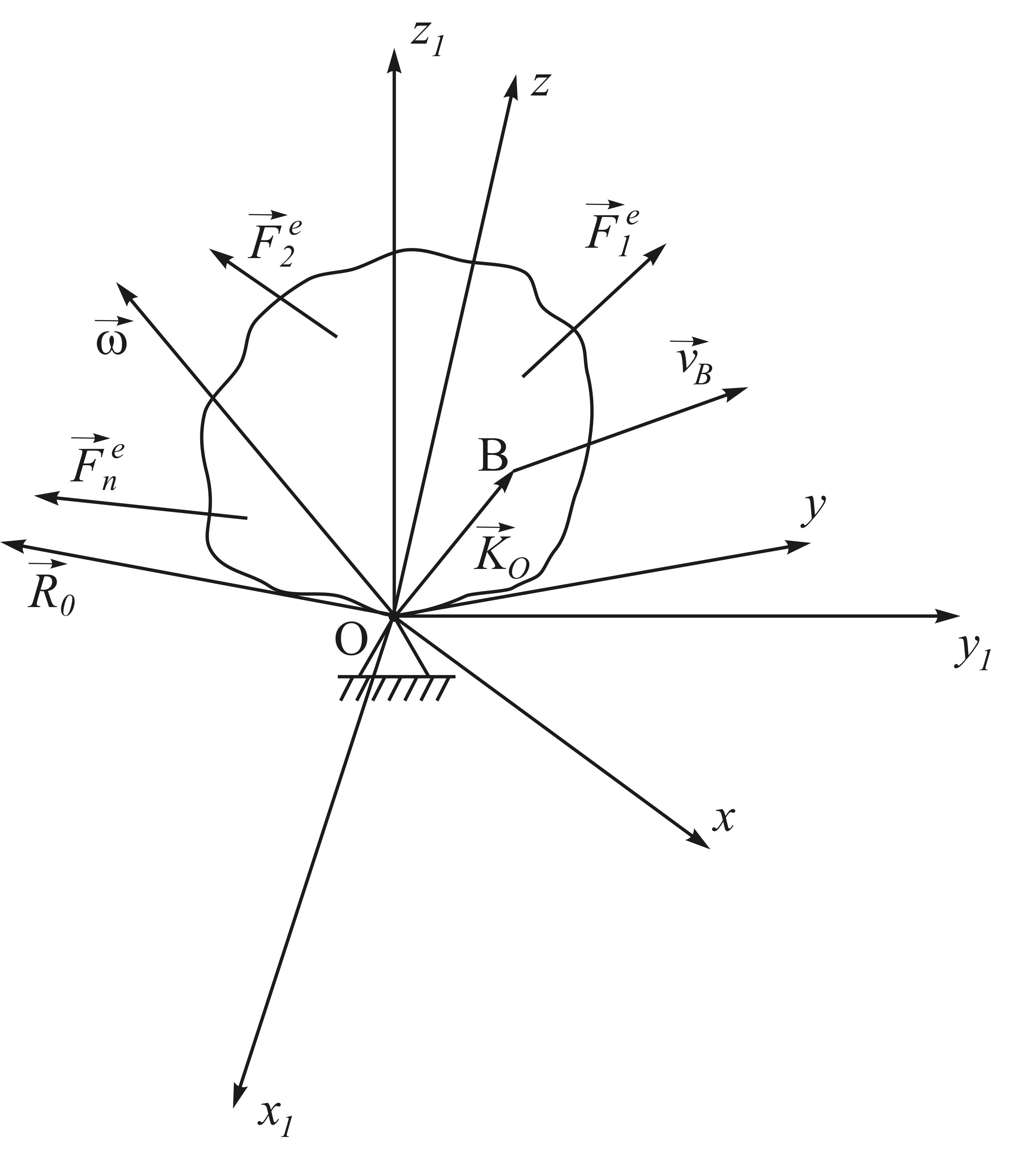
Рис. 37

Чтобы исключить из уравнений движения неизвестную реакцию , воспользуемся теоремой об изменении кинетического момента относительно центра, представив ее в виде (8.4), т.е. в виде теоремы Резаля. Тогда, поскольку, уравнение (8.4) даст

(8.5)

где , а- скорость по отношению к инерциальной системе отсчетаточки, совпадающей с концом вектора.

Движение тела изучается тоже по отношению к инерциальной системе отсчета . Но чтобы получить уравнения этого движения в наиболее простой форме проецируем обе части предыдущего равенства на жестко связанные с телом и движущиеся вместе с ним оси, являющиеся главными осями инерции тела для точки.

Тогда выражения проекций вектора будут иметь простой вид, а входящие в них моменты инерции, будут величинами постоянными.

Для вычисления абсолютной скорости на подвижные оси представимкак сумму относительной (по отношению к осям) скоростии переносной скорости. Тогда из уравнения (8.5)

и.

(8.6)

Обозначим координаты точки через. При этом, так как радиусом – вектором точкиявляется вектор, то.

Как указано в кинематике, при определении движение осейво внимание не принимается, следовательно, а при определенииточкуможно рассматривать как принадлежащую телу, связанному с осями. Но это тело движется вокруг неподвижной точки.

По аналогии с формулой Эйлера из кинематики , имеем

Заменяя в найденных выражениях ивеличины,,их значениями и подставляя эти значения,во второе из равенств (8.6), получим

Аналогичные выражения получаются для проекций первого из равенств (8.6) на оси и.

Так как для связанных с телом осей величиныпостоянны, то окончательно найдем следующие дифференциальные уравнения движения твердого тела вокруг неподвижной точки в проекциях на главные оси инерции тела для этой точки:

(8.7)

Уравнения (8.7) называются динамическими уравнениями Эйлера.

Дифференциальные уравнения движения свободного твердого тела.

Как известно, движение свободного твердого тела слагается из поступательного движения вместе с полюсом, в качестве которого при решении задач динамики выбирают обычно центр масс тела, и из движения вокруг центра масс, как вокруг неподвижной точки. Если на тело действуют внешние силы, то движение полюсаописывается теоремой о движении центра масс, где- масса тела.

В проекциях на неподвижные оси это равенство дает:

(8.8)

где - координаты центра масс тела.

Для движения же вокруг центра масс теорема об изменении кинетического момента дает в проекциях на главные центральные оси инерции тела три уравнения, совпадающие по виду с уравнениями (8.7). Таким образом, система дифференциальных уравнений (8.7), (8.8) описывает движение свободного твердого тела.

22. Начала аналитической механики

22.1 Введение

Аналитическую механику отличает общность аналитических методов постановки и решения задач механики. Будь то составление уравнений равновесия или движения механических систем, разыскание возможных положений равновесия или законов движения, исследование устойчивости равновесия или движения и т.д.

Основы аналитической механики были разработаны Ж. Лагранжем. В своем курсе, вышедшем в 1788 году он писал: «В этой работе совершенно отсутствуют какие бы то ни было чертежи. Излагаемые мною методы не требуют ни построений, ни геометрических или механических рассуждений; они требуют только алгебраических операций, подчиненных планомерному и однообразному ходу. Все любящие анализ с удовольствием убедятся в том, что механика становится новой отраслью анализа, и будут мне благодарны за то, что этим путем я расширил область его применения».

В основе аналитической механики лежат понятия связи, возможного перемещения и возможной работы. Определения, важные для последующего изложения, поясним, прибегнув к простому примеру.

Возьмем математический маятник – рис 38.

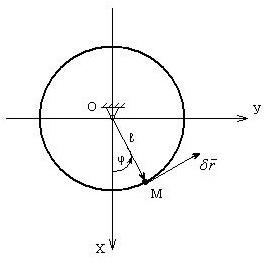
рис.38

Материальная точка с помощью безмассового жесткого стержня подвешена к центру вращения О. Понятно, что точка М несвободна. Её движение подчинено условию:

(9.1)

Данное условие является уравнением голономной (ограничения наложены на координаты (х, у) точки и на её положение), удерживающей (точка М не может ни удалиться от центра О, ни приблизиться к нему), стационарной (время tявно не входит в уравнение (9.1)) связи.

Если стержень заменить нитью, получим голономную, стационарную, неудерживающую связь (точка М не может удалиться от центра О, но может приближаться к нему). Неудерживающие связи записываются в виде неравенств. Наконец, если длина нити будет переменной, зависящей от времени l=l(t), связь будет голономной, неудерживающей, нестационарной. Есть вид связей, называемых неголономными, которые накладывают ограничения на скорости точек системы. В нашем курсе системы с такими связями не рассматриваются.

Продифференцируем уравнение (9.1) по времени:

.

Отсюда, заменив символ dна δ, получим:

(9.2)

Это условие называют варьированным уравнением связи. Оно накладывает ограничение, как на координаты, так и на приращения (вариации) координат.

Условие (9.2) можно представить в форме:

(9.3)

где - возможное (элементарное) перемещение точки М. Возможным перемещением точки называют бесконечно малое, воображаемое перемещение, совместимое со связями. Из (9.3) видно, что возможное перемещение точки М направлено по касательной к траектории.

Мы определили положение точки М с помощью координат x,yи ввели уравнение связи. Можно поступить иначе. Учтя связь, сразу определить положение точки М с помощью координаты (угла). Координаты, при введении которых непосредственно учитываются связи, называют обобщенными координатами. В голономной системе число обобщенных (независимых) координат равно числу степеней свободы.

Предположим, что на точку М действует система ,, … ,активных сил. Помимо них к точке приложена реакциясвязи (стержня). Возможной (элементарной) работой активных сил называют алгебраическую величину:

(9.4)

Аналогично – для реакции связи:

Но поскольку , то. Связь в нашем случае является идеальной. Связи называются идеальными, если возможная работа их реакции на любом возможном перемещении системы равна нулю.