20.4 Теорема об изменении кинетической энергии

Подобная теорема для одной материальной точки нам уже встречалась и выражалась равенством ( ). Для точки, входящей в систему, та же зависимость имеет вид:

.

Сложив почленно равенства, получим:

.

(7.14)

Дифференциал кинетической энергии системы равен сумме элементарных работ всех приложенных к точкам системы внешних и внутренних сил.

Интегрируя (7.14), получим теорему в конечной (интегральной) форме:

,

(7.15)

где - кинетическая энергия системы в ее начальном и конечном положениях. Изменение кинетической энергии системы при перемещении ее точек из некоторого начального положения в конечное равно алгебраической сумме работ сил внешних и внутренних.

Важно заметить, внутренние силы совершают работу лишь в изменяемых системах: в деформируемом теле, в автомобиле, - когда работает его двигатель, и т.д.

При составлении равенства (7.15) приходиться вычислять кинетическую энергию системы и работу приложенных сил. Первая часть задачи решается с помощью теоремы (формулы) Кенига.

,

(7.16)

где M– масса системы, - скорость центра масс, - скорость точек относительно центра масс.

Кинетическая энергия какой угодно системы в абсолютном движении равна кинетической энергии ее поступательного движения вместе с центром масс, сложенной с кинетической энергией движения относительно центра масс.

Кинетическая энергия абсолютно твердого тела при определенных видах его движения выражается формулами:

1. При поступательном движении

,

где V– скорость тела.

2. При вращении вокруг неподвижной оси

,

где - момент инерции,ω– угловая скорость.

3. При плоском движении

,

где - скорость центра масс, - момент инерции относительно оси, проходящей через центр масс (величина постоянная).

4. При произвольном движении

,

где - момент инерции тела относительно мгновенной оси (переменный).

Для вычисления работы совокупности сил не существует всеобъемлющей формулы, подобной формуле Кенига. Это объясняется многообразием сил природы. Но есть категория сил, называемых потенциальными, работа которых не зависит от закона движения системы и выражается наперед заданными формулами.

Положим, что на систему действуют силы, зависящие только от положения материальных точек, причем так, что

.

Вводимую таким образом функцию П называют потенциальной энергией силового поля, само поле – потенциальным, а сами силы называют потенциальными силами.

Сумма элементарных работ потенциальных сил равна:

(7.17)

где dП – полный дифференциал потенциальной энергии.

Интегрируя (7.17), получим

.

(7.18)

Потенциальная энергия есть работа, совершаемая потенциальными силами при переходе (перемещении) системы из заданного (отклоненного) положения в начальное (нулевое).

Если (7.18) подставим в (7.15), то получим равенство

,

(7.19)

выражающее закон сохранения механической энергии.

При движении системы в потенциальном силовом поле ее полная механическая энергия не изменяется (сохраняется). По этой причине поле сил называют консервативным, а сами силы – консервативными.

Потенциальными (консервативными) силами являются: силы тяжести, силы упругости, силы тяготения.

Пусть плоскость Оху горизонтальна, находиться на поверхности земли и определяет нулевой уровень, , осьOzнаправлена по вертикали вверх. Для тяжелой материальной точки, находящейся на высотеz, потенциальная энергия силы тяжести равна

,

где G– вес точки.

Точки с таким запасом работы, образуют плоскость, параллельную плоскости Оху.

Пусть упругая пружина удлиняется в направлении оси Ох на х (ее конец в натуральном состоянии совпадает с началом координат). Потенциальная энергия силы упругости равна:

,

где C– коэффициент жесткости.

Точки с одинаковым запасом работы лежат на сфере радиуса xс центром в начале координат.

При вычислении правой части равенства (7.15) не столь важно внешние ли это силы или внутренние. Принципиально важно знать, совершают они работу или нет. С этой точки зрения при использовании теоремы (7.15) силы подразделяют на активные и реакции связей. К активным относятся те, которые совершают работу, к реакциям – те, которые работы не совершают. Сила трения скольжения является реакцией в статическом смысле, но она относится к активным силам. Реакция гладкой поверхности является реакцией в динамическом смысле, ее работа в отдельности равна нулю. Силы связи в абсолютно твердом теле являются реакциями, так как их работа в совокупности равна нулю. В этом заключается динамическое определение реакции связей. Вообще, связи, реакции которых работы не совершают, называют идеальными связями.

Примеры.

1.Механическая система состоит из груза, трубы и блока, связанных гибкой нерастяжимой нитью. Груз опускается, труба катится без скольжения. Определить скорость и ускорение груза, в тот момент, когда он пройдет расстояние Н. Движение начинается из состояния покоя. Дано: М – масса груза,mиR– масса и радиус трубы, - момент сопротивления (постоянный). Массой блока и нити пренебречь.

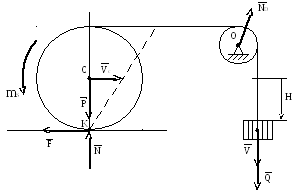
Рис. 30

Воспользуемся теоремой

.

По условию задачи . Тела, входящие в систему, абсолютно твердые, а нить гибкая и нерастяжимая. Следовательно, .

Внешние силы: и реакции работы не совершают. Остается раскрыть равенство

.

Кинетическая энергия

.

Здесь ,,.

Окончательно

. (1)

Работа силы равнаQH. Работа пары сил равна произведению ее момента на угол поворота трубы - .

Полная работа

. (2)

Приравнивая (1) и (2), получаем равенство

. (3)

Отсюда

.

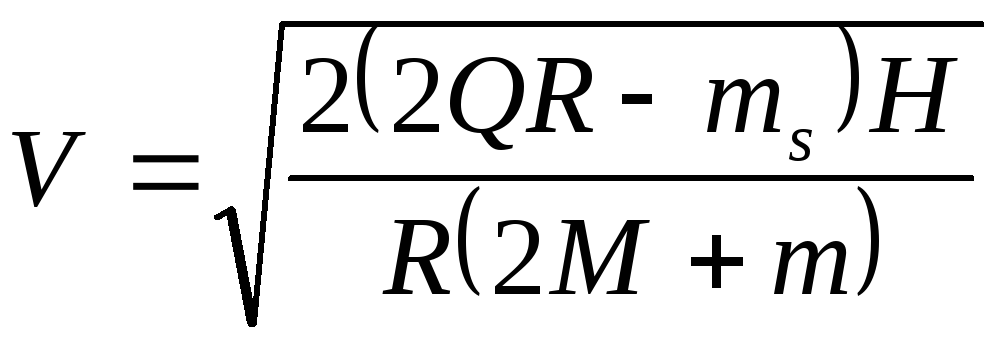Чтобы определить ускорение, продифференцируем по времени обе части равенства (3). Получим:

.

Отсюда, замечая, что , находим

.

2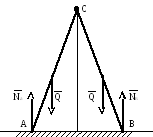.Два стержня равной длины 2и массыmсочлены в точке С и устанавливаются на гладкой горизонтальной плоскости. Расстояние шарнира С до пола равно Н. Центры масс стержня относительно оси, проходящей через центр масс, равенρ. В некоторый момент времени система опускается и начинает падать. Определить скорость шарнира С в момент удара его о пол.

Рис. 31

Воспользуемся теоремой

.

Движение начинается из состояния покоя, а потому . Стержни абсолютно твердые, трение в шарнире отсутствует. Следовательно, .

Остается раскрыть равенство:

.

Внешними силами, действующими на систему, являются силы тяжести и реакции плоскости. Сумма их проекций на горизонтальное направление равна нулю. Это свидетельствует о том, что центр масс системы по горизонтали не перемещается и «падает» по прямой СД. В момент касания плоскости каждый стержень вращается вокруг своего свободного конца. Кинетическая энергия системы в этом положении равна

,

где - момент инерции стержня относительно конца, - скорость шарнира С, - мгновенная угловая скорость стержня.

Работу совершают лишь силы тяжести

.

Приравнивая кинетическую энергию работе сил, получим:

.

Отсюда

.