20.3 Теорема об изменении кинетического момента

Как уже сказано, данная теорема определяет закон вращения системы. Вернемся к рис. 25 и назовем кинетическим моментом системы относительно точки О векторную величину:

, (7.11)

где - кинетический момент относительно центра масс. Подобно тому как в динамике одной материальной точки запишем теорему моментов для точки, входящей в систему.

.

Просуммировав по всем точкам и приняв во внимание свойство внутренних сил, получим окончательно:

(7.12)

Производная по времени от кинетического момента системы относительно неподвижного центра равна главному моменту внешних сил.

Представим (7.11) в виде:

Отсюда, как нетрудно показать, следует теорема для относительного движения:

(7.13)

Здесь кинетический момент и момент сил вычисляются относительно центра масс. Теорема формулируется как и в предыдущем случае. Если в (7.12) или (7.13) правую часть обратить в нуль, то придем к законам сохранения кинетического момента, заключающегося в неизменности вектора или.

Формулой (7.12) удобно пользоваться, когда движение системы представляется как одно вращение вокруг некоторого центра, например, в динамике твердого тела с одной неподвижной точкой. Формула (7.13) более удобна, когда движение системы представляется как сложное, состоящее из поступательного и вращения; например, в динамике самолета, автомобиля и т.д. Уравнение вращения самолета в полете было бы неудобно записывать относительно точки, которая находиться на земле.

Спроектируем ( 7.12 ) на направление Оz, получим теорему в скалярной форме:

Отсюда, в случае , находим закон сохранения:

Если внешние силы не создают вращающего момента вокруг оси Оz, то кинетический момент системы относительно этой оси остается неизменным.

Примеры

1.Задача Н.Е. Жуковского. Однородный брусок длиныlи массыMопирается на гладкий пол и гладкую стену. По бруску сбегает акробат, масса которогоm. Спрашивается, как, по какому закону должен бежать акробат (если принять его за материальную точку), чтобы брусок оставался неподвижным? Уголθнаклона бруска к полу задан.

Введем координатную ось As. Пустьs– координата материальной точки,

- скорость; тогда произведениеmбудет количеством движения всей системы (поскольку брусок неподвижен).

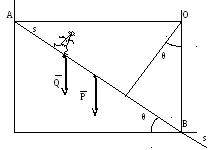
Рис. 28

Реакции пола и стены проходят через точку О, которая также остается неподвижной. Запишем теорему об изменении кинетического момента системы относительно точки О:

.

Отсюда находим дифференциальное уравнение движения:

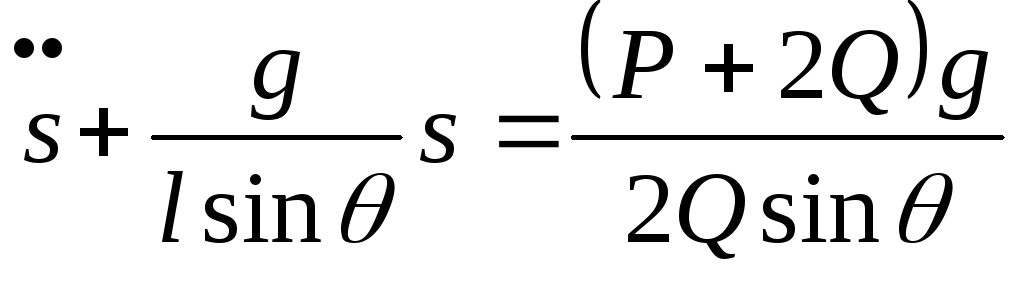. (1)

Как видим, акробат должен бежать по тому же закону, по какому движется материальная точка такой же массы под действием постоянной силы

,

направленной в положительную сторону оси As, и переменной силы

,

подобной силе упругости пружины жесткости , направленной к началу координат. Уравнение (1) имеет общее решение:

.

При нулевых начальных условиях акробат должен бежать по закону:

,

2.Карусель может вращаться без трения вокруг вертикальной осиAz. На карусели стоит человек. В некоторый момент времени он начинает идти по окружности радиусаRсо скоростью (относительно карусели). Определить угловую скоростьωвращения карусели, если масса человекаm, а момент инерции карусели .

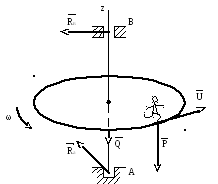
Внешними силами, действующими на систему, являются силы тяжести и реакции подшипников. Так как силы тяжести параллельны оси вращения, а реакции пересекают эту ось, то сумма моментов

.

Следовательно, имеет место закон сохранения кинетического момента

.

Но в начальный момент система находилась в покое, так что равенство выполняется при любом времени.

Пусть - кинетический момент карусели, - кинетический момент человека. Кинетический момент системы:

.

Отсюда находим угловую скорость вращения карусели:

.

Знак минус свидетельствует о том, что карусель будет вращаться в направлении, противоположном показанном на рисунке.