19.4. Центробежные моменты инерции. Понятие о главных осях инерции тела

Центробежными моментами инерции называются величины ,,, определяемые равенствами,,, где

- массы точек;,,- их координаты; при этом,,

Центробежные моменты инерции могут быть как положительными, так и отрицательными величинами, и в частности при определенным образом выбранных осях могут обращаться в нули.

Рассмотрим однородное тело, имеющее ось симметрии (рис. 24)

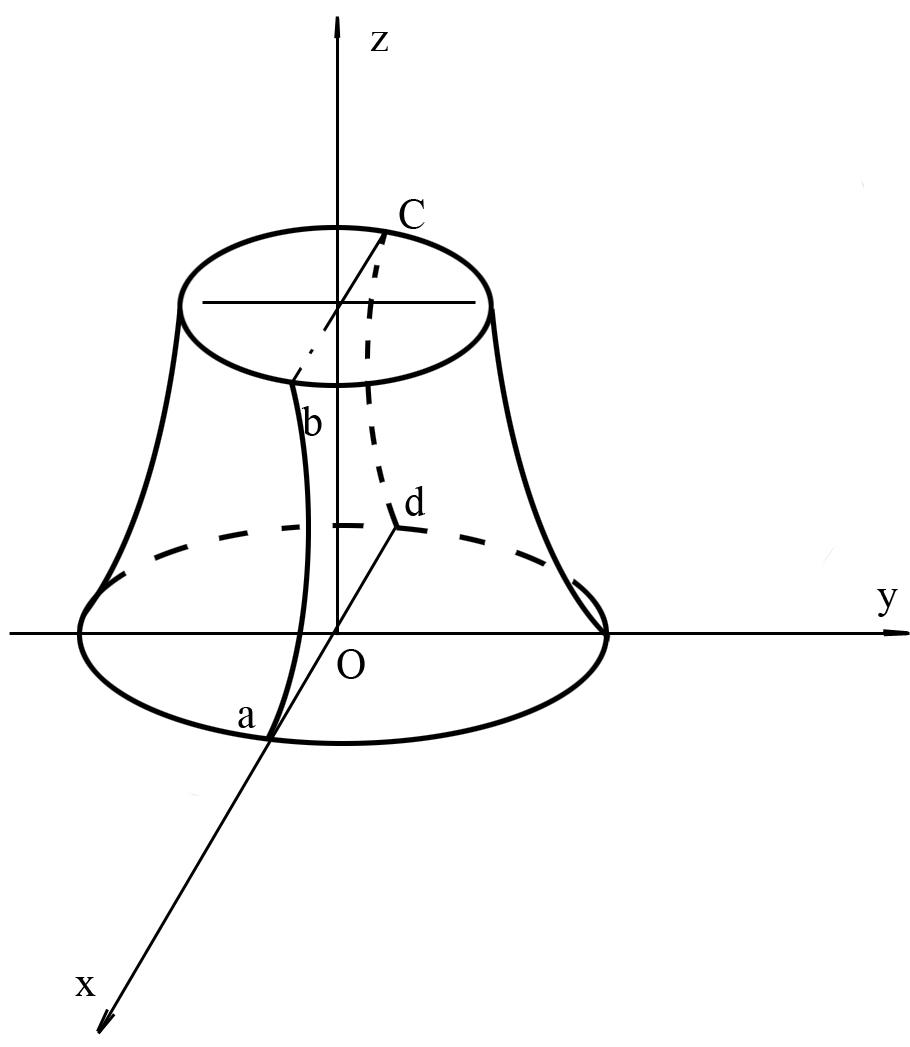
Рис. 24

Проведем координаты оси так, чтобы ось была направлена вдоль оси симметрии. Тогда в силу симметрии каждой точки тела с массойи координатами,,будет соответствовать точка с другим индексом, но с такой же массой и с координатами равными,,. В результате получим, чтои. Тогда,.

Ось , для которой центробежные моменты инерции,, содержащие в своих индексах наименование этой оси равна нулю, называется главной осью инерции тела для точки.

Из изложенного следуем, что если тело имеет ось симметрии, то эта ось является главной осью инерции тела для любой своей точки.

Главная ось инерции не обязательно является осью симметрии. Рассмотрим однородное тело, имеющее плоскость симметрии (на рис. 24 плоскостью симметрии тела является плоскость ).

Проведем в этой плоскости какие-нибудь оси ,и перпендикулярную им ось

. Тогда в силу симметрии каждой точке с массойи координатами, равными,,, будет соответствовать точка с такой же массой и координатами, равными,,. В результате, как и в предыдущем случае, найдем, чтоиили,, откуда следует, что осьявляется главной осью инерции для точки. Таким образом, если тело имеет плоскость симметрии, то любая ось, перпендикулярная этой плоскости, будет главной осью инерции тела для точки, в которой ось пересекает плоскость симметрии.

Равенства ,выражают условия того, что осьявляется главной осью инерции тела для точки(начала координат). Аналогично, если,, то осьбудет для точкиглавной осью инерции. Следовательно, если все центробежные моменты инерции равны нулю, т.е,,, то каждая из координатных осейявляется главной осью инерции тела для точки(начала координат).

Моменты инерции тела относительно главных осей инерции называются главными моментами инерции, построенные для центра масс тела, называют главными центральными осями инерции тела. Из доказанного выше следует, что если тело имеет ось симметрии, то эта ось является одной из главных центральных осей инерции тела, так как центр масс тела лежит на этой оси. Если же тело имеет плоскость симметрии, то ось, перпендикулярная этой плоскости и проходящая через центр масс тела, будет также одной из главных центральных осей инерции тела.

20. Общие теоремы динамики системы

20.1 Вводные определения и дифференциальные уравнения движения

Системой материальных точек или механической системой, или просто системой называют совокупность материальных точек, движения которых взаимно зависимы. Неизменяемую систему точек называют абсолютно твердым телом. Система может состоять из совокупности твердых тел.

Систему называют свободной, если для ее точек возможны всякие движения, и называют несвободной, если есть некоторые ограничения, так что не всякие движения (положения) точек становятся возможными. Эти ограничения, стесняющие свободу движения, называют связями.

В динамике системы различают силы внешние и внутренние. Внешние – это воздействия на систему сторонних объектов, внутренние – силы взаимодействия между отдельными точками системы. Как те, так и другие могут быть задаваемыми и реакциями связей. Силы реакций исчезают вместе с исчезновением связей. При этом задаваемые остаются.

Представим себе движущуюся систему из Nматериальных точек. Пусть- массы точек. Обратим внимание на точкуMk . (рис. 25)

Рис. 25

Здесь: - равнодействующие внешних и внутренних сил,- скорость и ускорение точки,,,- радиусы-векторы, смысл которых виден непосредственно из рисунка, О – неподвижный центр, С – центр масс системы.

Центром масс системы называют геометрическую точку, положение которой определяется равенством:

(7.1)

где - масса системы.

Если в (7.1) обе части умножить на g(ускорение тяжести), то вместо масс будем иметь силы тяжести. Следовательно, при одинаковых для всех точек системы ускоренияхgцентр масс совпадает с центром тяжести. Отнеся (7.1) к координатной системе, получим координаты точки С.

и две других координаты.

Продифференцируем в (7.1) обе части по времени (последовательно два раза), получим:

,(7.2)

где - скорость и ускорение центра масс. Равенства (7.2) играют важную роль в динамике системы.

Теперь запишем основной закон динамики для каждой материальной точки. Таким образом мы придем к дифференциальным уравнениям движения системы в векторной форме:

(7.3)

В проекциях будем иметь 3Nуравнений в скалярной форме:

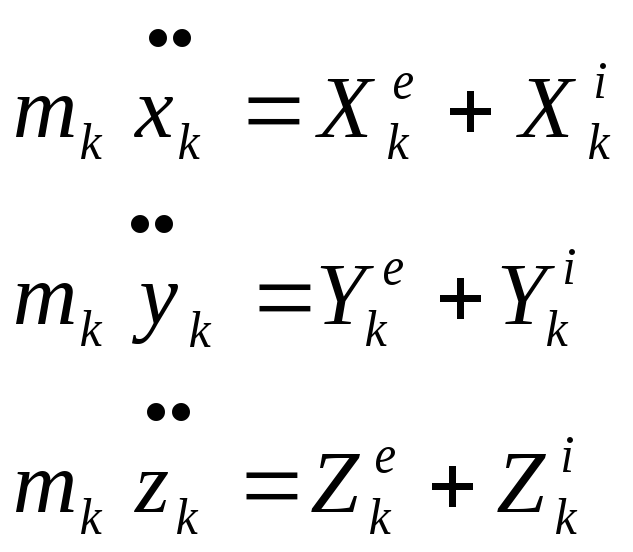
Здесь важно иметь в виду основное свойство внутренних сил: их главный вектор и главный момент (в силу третьего закона Ньютона) равны нулю, т.е.:

(7.4)

Но это не означает, что внутренние силы не влияют на движение материальных точек системы. Например, когда акробат находится в свободном полете, отдельные части его тела могут производить довольно замысловатые действия. Они выполняются внутренними силами. В то же время центр масс акробата движется по параболе, и это движение не подвержено влиянию внутренних сил.

Важными следствиями уравнений (7.3) являются общие теоремы динамики, которыми устанавливаются зависимости между некоторыми суммарными мерами движения системы и суммарными мерами действия приложенных сил. Таких теорем четыре: об изменение количества движения, о движение центра масс, об изменении кинетического момента и об изменении кинетической энергии. Первые три теоремы замечательны тем, что позволяют исключить из динамических соотношений внутренние силы; последняя позволяет исключить силы, не совершающие работы при перемещениях точек системы.