
4 Традиционные симметричные криптосистемы
Ктрадиционным относятся следующие криптосистемы:
шифры замены (подстановки):
а) шифры простой замены (одноалфавитные подстановки); б) шифры сложной замены ( многоалфавитные подстановки) в)многоалфавитная одноконтурная монофоническая; г)многоалфавитная многоконтурная.
шифрование методом перестановки:
а) простая; б) простая по ключу по таблице; в) двойная;
в) усложненная по маршрутам.
шифрование методом гаммирования:
а) с конечной короткой гаммой; б) с конечной длинной гаммой; в) с бесконечной гаммой.
шифрование с помощью аналитических преобразований:
а) матричные; б) по особым зависимостям.
комбинированные методы шифрования:
а)подстановка+перестановка; б)подстановка+гаммирование; в)перестановка+гаммирование; г)гаммирование+гаммирование.
4.1 Шифры замены (подстановки)
При шифровании заменой (подстановкой) символы шифруемого текста заменяются символами того же или другого алфавита по заранее установленным правилам замены.
82
4.1.1 Шифры простой замены (одноалфавитные подстановки)
В шифрах простой замены каждый символ исходного текста заменяется символами того же или другого алфавита одинаково на всем протяжении текста. Часто шифры простой замены называют шифрами одноалфавитной подстановки.
Примеры таблиц замены:
АБ В Г Д Е Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш Щ Ь Ы Ъ Э Ю Я М Л Д О Т В А Ч К Е Ж Х Щ Ф Ц Э Г Б Я Ъ Ш Ы З И Ь Н Ю У П С Р Й
АБ В Г Д Е Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш Щ Ь Ы Ъ Э Ю Я
Q W E R T Y U I O P [ ] A S D F G H J K L Z X C V B N M < > @ %
Стойкость метода простой замены низкая. Зашифрованный текст имеет те же
самые статистические характеристики, что и исходный, поэтому зная стандартные частоты появления символов в том языке, на котором написано сообщение, и подбирая по частотам появления символы в зашифрованном сообщении, можно восстановить таблицу замены. Для этого требуется лишь достаточно длинный зашифрованный текст, для того, чтобы получить достоверные оценки частот появления символов. Поэтому простую замену используют лишь в том случае, когда шифруемое сообщение достаточно короткое.
Стойкость метода равна 20 - 30, трудоемкость определяется поиском символа в таблице замены. Для снижения трудоемкости при шифровании таблица замены сортируется по шифруемым символам, а для расшифровки формируется таблица дешифрования, которая получается из таблицы замены сортировкой по заменяющим символам.
4.1.1.1Шифрование на основе полибианского квадрата Полибианский квадрат изображён на рисунке 4.1.
Для шифровании в этом полибианском квадрате находили очередную букву открытого текста и записывали в шифртекст букву, расположенную ниже неё в том же столбце. Если буква текста оказывалась в нижней строчке таблицы, то для шифртекста брали самую верхнюю букву из того же столбца.
83
Пример. Зашифровать сообщение с помощью полибианского квадрата. В этом случае шифртекст имеет вид .
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рисунок 4.1-Квадрат Полибия (полибианский квадрат) 4.1.1.2 Система шифрования Цезаря
Шифр Цезаря является частным случаем шифра простой замены (одноалфавитной подстановки). При шифровании исходного текста каждая буква заменялась на другую букву того же алфавита по следующему правилу. Заменяющая буква определялась путём смещения по алфавиту от исходной буквы на К букв. При достижении конца алфавита выполнялся циклический переход к его началу. Цезарь использовал шифр замены при смещении К=3. Такой шифр замены можно задать таблицей подстановок, содержащей соответствующие пары букв открытого текста и шифртекста.
A D |
J M |
S V |
B E |
K N |
T W |
C F |
L O |
U X |
D G |
M P |
V Y |
E H |
N Q |
W Z |
F I |
O R |
X A |
G J |
P S |
Y B |
H K |
Q T |
Z C |
I L |
R U |
|
|
|
|
Рисунок 4.2 - Таблица подстановок Цезаря
Пример. Зашифровать послание Цезаря:VENI VIDI VICI. Используя таблицу подстановок (рисунок 4.2) получаем шифртекст:
YHQL YLGL YLFL
84

4.1.1.3 Система Цезаря с ключевым словом Система шифрования Цезаря с ключевым словом является одноалфа-
витной системой подстановок. Особенностью этой системы является использование ключевого слова для смещения и изменения порядка символов в алфавите подстановок.
Пример. Зашифровать сообщение SEND MORE MONEY по системе Цезаря с ключевым словом DIPLOMAT.
Решение. Выберем некоторое число k, 0 k < 25. Ключевое слово записывается под буквами алфавита, начиная с буквы, числовой код которой
совпадает с |
выбранным числом k: |
|
|
|
0 1 2 3 4 5 |
10 |
15 |
20 |
25 |
A B CD E F G H I J K L M NO P QR S T U V W XY Z
D I P L O M A T
Оставшиеся буквы алфавита подстановки записываются после ключевого слова в алфавитном порядке:
5
A B CD E F G H I J K L MN O P Q R S T U VWX Y Z VWXY ZD I P L OMA T B C E F G H J K N Q R S U
Теперь мы имеем таблицу подстановкок для каждой буквы произвольного сообщения. Используя эту таблицу, исходное сообщение SEND MORE MONEY шифруется как HZBY TCGZ TCBZS.
Достоинством системы Цезаря с ключевым словом является то, что количество возможных ключевых слов практически неисчерпаемо. Недостатком этой системы является возможность взлома шифртекста на основе анализа частот появления букв.
4.1.1.4Шифрующие таблицы Трисемуса
В1508 г. аббат из Германии Иоганн Трисемус написал печатную работу по криптологии под названием "Полиграфия". В этой книге он впервые сис-
85
тематически описал применение шифрующих таблиц, заполненных алфавитом в случайном порядке. Для получения такого шифра замены обычно использовались таблица для записи букв алфавита и ключевое слово (или фраза). В таблицу сначала вписывалось по строкам ключевое слово, причем повторяющиеся буквы отбрасывались. Затем эта таблица дополнялась не вошедшими в нее буквами алфавита по порядку. При шифровании находят в этой таблице очередную букву открытого текста и записывают в шифртекст букву, расположенную ниже неё в том же столбце. Если буква текста оказывается в нижней строке таблицы, тогда для шифртекста берут самая верхнюю букву из того же столбца.
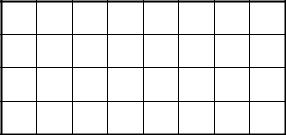
Поясним этот метод шифрования на примере. Для русского алфавита шифрующая таблица может иметь размер 4 8. В качестве ключа выберем слово БАНДЕРОЛЬ. Шифрующая таблица с таким ключом показана на рисунке 4.3.
Б |
А |
Н |
Д |
Е |
Р |
О |
Л |
Ь |
В |
Г |
Ж |
З |
И |
Й |
К |
М |
П |
С |
Т |
У |
Ф |
Х |
Ц |
Ч |
Ш Щ |
Ы |
Ъ |
Э |
Ю |
Я |
|
Рисунок 4.3 - Шифрующая таблица Трисемуса с ключевым словом БАНДЕРОЛЬ
Допустим, что с помощью таблицы Трисемуса нужно зашифровать сообщение ВЫЛЕТАЕМПЯТОГО. Используя эту таблицу в соответствии с вышеизложенной методикой, получаем шифртекст ПДКЗЫВЗЧШЛЫЙСЙ.
Такие табличные шифры называются монограммными, так как шифрование выполняется по одной букве. Трисемус первым заметил, что шифрующие таблицы позволяют шифровать сразу по две буквы. Такие шифры назы-
ваются биграммными.
4.1.1.5 Биграммный шифр Плейфейра Шифр Плейфейра, изобретенный в 1854 г., является наиболее извест-
ным биграммным шифром замены. Он применялся Великобританией во вре-
86
мя первой мировой войны. Основой шифра Плейфейра является шифрующая таблица со случайно расположенными буквами алфавита исходных сообщений. Для удобства запоминания шифрующей таблицы отправителем и получателем сообщений можно использовать ключевое слово (или фразу) при заполнении начальных строк таблицы. В целом структура шифрующей таблицы системы Плейфейра полностью аналогична структуре шифрующей таблицы Трисемуса. Поэтому для пояснения процедур шифрования и расшифрования в системе Плейфейра воспользуемся шифрующей таблицей Трисемуса из предыдущей задачи ( рисунок 4.3).
Процедура шифрования включает следующие шаги.
1.Открытый текст исходного сообщения разбивается на пары букв (биграммы). Текст должен иметь четное количество букв и в нем не должно быть биграмм, содержащих две одинаковые буквы. Если эти требования не выполнены, то текст модифицируется даже из-за незначительных орфографических ошибок.
2.Последовательность биграмм открытого текста преобразуется с помощью шифрующей таблицы в последовательность биграмм шифртекста по следующим правилам:
2а.Если обе буквы биграммы открытого текста не попадают на одну строку или столбец (как, например, буквы А и Й в табл. на рис.2.6), тогда находят буквы в углах прямоугольника, определяемого данной парой букв. (В нашем примере это – буквы АЙОВ. Пара букв АЙ отображается в пару ОВ. Последовательность букв в биграмме шифртекста должна быть зеркально расположенной по отношению к последовательности букв в биграмме открытого текста.)
2б.Если обе буквы биграммы открытого текста принадлежат одному столбцу таблицы, то буквами шифртекста считаются буквы, которые лежат под ними. (Например, биграмма НС дает биграмму шифртекста ГЩ.) Если при этом буква открытого текста находится в нижней строке, то для шифртекста берется соответствующая буква из верхней строки
87
того же столбца. (Например, биграмма ВШ дает биграмму шифртекста ПА.)
2в.Если обе буквы биграммы открытого текста принадлежат одной строке таблицы, то буквами шифртекста считаются буквы, которые лежат справа от них. (Например, биграмма НО дает биграмму шифртекста ДЛ.) Если при этом буква открытого текста находится в крайнем правом столбце, то для шифра берут соответствующую букву из левого столбца в той же строке. (Например, биграмма ФЦ дает биграмму шифртекста ХМ.)
Зашифруем биграммным шифром Плейфера текст
ВСЕ ТАЙНОЕ СТАНЕТ ЯВНЫМ
Разобьём этот текст на биграммы:
ВС ЕТ АЙ НО ЕС ТА НЕ ТЯ ВН ЫМ
Данная последовательность биграмм открытого текста преобразуется с помощью шифрующей таблицы (рисунок 4.3) в следующую последовательность биграмм шифртекста
ГП ДУ ОВ ДЛ НУ ПД ДР ЦЫ ГА ЧТ
При расшифровании применяется обратный порядок действий. Шифрование биграммами резко повышает стойкость шифров к вскрытию.
Хотя книга И.Трисемуса "Полиграфия" была относительно доступной, описанные в ней идеи получили признание лишь спустя три столетия. По всей вероятности, это было обусловлено плохой осведомленностью криптографов о работах богослова и библиофила Трисемуса в области криптографии.
4.1.2 Шифры сложной замены ( многоалфавитные подстановки)
Шифры сложной замены называют многоалфавитными, так как для шифрования каждого символа исходного сообщения применяют свой шифр простой замены. Многоалфавитная подстановка последовательно и циклически меняет используемые алфавиты. Для замены символов используются несколько алфавитов, причем смена алфавитов проводится последовательно и циклически: первый символ заменяется на соответствующий символ первого алфавита, второй - из
88
второго алфавита, и т.д. пока не будут исчерпаны все алфавиты. После этого использование алфавитов повторяется.
4.1.2.1 Многоалфавитная одноконтурная обыкновенная подстановка Рассмотрим шифрование с помощью таблицы Вижинераквадратной матрицы
с n2 элементами, где n - число символов используемого алфавита. В первой строке матрицы содержится исходный алфавит, каждая следующая строка получается из предыдущей циклическим сдвигом влево на один символ (рисунок 4.4).
А Б В Г Д Е Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш Щ Ь Ы Ъ Э Ю Я Б В Г Д Е Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш Щ Ь Ы Ъ Э Ю Я А В Г Д Е Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш Щ Ь Ы Ъ Э Ю Я А Б
ГД Е Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш Щ Ь Ы Ъ Э Ю Я А Б В Д Е Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш Щ Ь Ы Ъ Э Ю Я А Б В Г Е Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш Щ Ь Ы Ъ Э Ю Я А Б В Г Д Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш Щ Ь Ы Ъ Э Ю Я А Б В Г Д Е
ЗИ Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш Щ Ь Ы Ъ Э Ю Я А Б В Г Д Е Ж И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш Щ Ь Ы Ъ Э Ю Я А Б В Г Д Е Ж З Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш Щ Ь Ы Ъ Э Ю Я А Б В Г Д Е Ж З И К Л М Н О П Р С Т У Ф Х Ц Ч Ш Щ Ь Ы Ъ Э Ю Я А Б В Г Д Е Ж З И Й Л М Н О П Р С Т У Ф Х Ц Ч Ш Щ Ь Ы Ъ Э Ю Я А Б В Г Д Е Ж З И Й К М Н О П Р С Т У Ф Х Ц Ч Ш Щ Ь Ы Ъ Э Ю Я А Б В Г Д Е Ж З И Й К Л Н О П Р С Т У Ф Х Ц Ч Ш Щ Ь Ы Ъ Э Ю Я А Б В Г Д Е Ж З И Й К Л М О П Р С Т У Ф Х Ц Ч Ш Щ Ь Ы Ъ Э Ю Я А Б В Г Д Е Ж З И Й К Л М Н П Р С Т У Ф Х Ц Ч Ш Щ Ь Ы Ъ Э Ю Я А Б В Г Д Е Ж З И Й К Л М Н О Р С Т У Ф Х Ц Ч Ш Щ Ь Ы Ъ Э Ю Я А Б В Г Д Е Ж З И Й К Л М Н О П С Т У Ф Х Ц Ч Ш Щ Ь Ы Ъ Э Ю Я А Б В Г Д Е Ж З И Й К Л М Н О П Р Т У Ф Х Ц Ч Ш Щ Ь Ы Ъ Э Ю Я А Б В Г Д Е Ж З И Й К Л М Н О П Р С У Ф Х Ц Ч Ш Щ Ь Ы Ъ Э Ю Я А Б В Г Д Е Ж З И Й К Л М Н О П Р С Т Ф Х Ц Ч Ш Щ Ь Ы Ъ Э Ю Я А Б В Г Д Е Ж З И Й К Л М Н О П Р С Т У Х Ц Ч Ш Щ Ь Ы Ъ Э Ю Я А Б В Г Д Е Ж З И Й К Л М Н О П Р С Т У Ф Ц Ч Ш Щ Ь Ы Ъ Э Ю Я А Б В Г Д Е Ж З И Й К Л М Н О П Р С Т У Ф Х Ч Ш Щ Ь Ы Ъ Э Ю Я А Б В Г Д Е Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ш Щ Ь Ы Ъ Э Ю Я А Б В Г Д Е Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Щ Ь Ы Ъ Э Ю Я А Б В Г Д Е Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш Ь Ы Ъ Э Ю Я А Б В Г Д Е Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш Щ Ы Ъ Э Ю Я А Б В Г Д Е Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш Щ Ь Ъ Э Ю Я А Б В Г Д Е Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш Щ Ь Ы Э Ю Я А Б В Г Д Е Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш Щ Ь Ы Ъ Ю Я А Б В Г Д Е Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш Щ Ь Ы Ъ Э Я А Б В Г Д Е Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш Щ Ь Ы Ъ Э Ю
Рисунок 4.4- Таблица Вижинера для русского алфавита
89
Система Вижинера подобна такой системе шифрования Цезаря, у которой ключ подстановки меняется от буквы к букве.
Для шифрования необходимо задать ключ - слово с неповторяющимися символами. Таблицу замены получают следующим образом: строку "Символы шифруемого текста" формируют из первой строки матрицы Вижинера, а строки из раздела "Заменяющие символы" образуются из строк матрицы Вижинера, первые символы которых совпадают с символами ключевого слова.
При шифровании исходного сообщения его выписывают в строку, а под ним записывают ключевое слово или фразу. Если ключ оказался короче сообщения, то его циклически повторяют. В процессе шифрования находят в верхней строке таблицы очередную букву исходного текста и в левом столбце очередное значение буквы ключа. Очередная буква шифртекста находится на пересечении столбца, определяемого шифруемой буквой, и строки, определяемой буквой ключа.
Рассмотрим пример получения шифртекста с помощью таблицы Вижинера. Пусть выбрано ключевое слово АМБРОЗИЯ. Нужно зашифровать сообщение ПРИЛЕТАЮ СЕДЬМОГО.
Выпишем исходное сообщение в строку и запишем под ним ключевое слово с повторением. В третью строку будем выписывать буквы шифртекста, опреде-
ляемые из таблицы Вижинера. |
|
|
Сообщение П Р И Л Е Т А Ю |
С Е Д Ь М О Г О |
|
Ключ |
А М Б Р О З И Я |
А М Б Р О З И Я |
Шифртекст П Ъ Й Ы УЩИ Э |
С С Е К Ь Х Л Н |
|
При шифровании и дешифровании нет необходимости держать в памяти всю матрицу Вижинера, поскольку используя свойства циклического сдвига, можно легко вычислить любую строку матрицы по ее номеру и первой строке.
При шифровании символы из первой строки заменяются символами остальных строк по правилу
a(1,i) -> a(k,i),
где k - номер используемой для шифрования строки.
90
Используя свойства циклического сдвига влево элементы k-ой строки можно выразить через элементы первой строки
a(1,i+k-1), если i<=n-k+1
a(k,i)=
a(1,i-n+k-1), если i>n-k+1
При дешифровании производится обратная замена a(k,i) -> a(1,i).
Поэтому необходимо решить следующую задачу: пусть очередной дешифруемый символ в тексте - a(1,j) и для дешифрования используется k-я строка матрицы Вижинера. Необходимо найти в k-ой строке номер элемента, равного a(1,j). Очевидно,
a(k,j-k+1), если j>=k
a(1,j)=
a(k,n-k+j+1), если j<k
Таким образом при дешифровании по k-ой строке матрицы Вижинера символа из зашифрованного текста, значение которого равно a(1,j), проводится обратная подстановка
a(1,j-k+1), если j>=k
a(1,j) ->
a(1,n-k+j+1), если j<k
Стойкость метода равна стойкости метода подстановки, умноженной на количество используемых при шифровании алфавитов, т.е. на длину ключевого слова и равна 20*L, где L - длина ключевого слова.
С целью повышения стойкости шифрования предлагаются следующие усовершенствования таблицы Вижинера:
во всех (кроме первой) строках таблицы буквы располагаются в произвольном порядке;
в качестве ключа используются случайные последовательности чисел, которые задают номера используемых строк матрицы Вижинера.
91
4.1.2.2 Многоалфавитная одноконтурная монофоническая подстановка
В монофонической подстановке количество и состав алфавитов выбирается таким образом, чтобы частоты появления всех символов в зашифрованном тексте были одинаковыми. При таком положении затрудняется криптоанализ зашифрованного текста с помощью его статистической обработки. Выравнивание частот появления символов достигается за счет того, что для часто встречающихся символов исходного текста предусматривается большее число заменяющих символов, чем для редко встречающихся.
Пример таблицы монофонической замены:
А Б В Г Д Е Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш Щ Ь Ы Ъ Э Ю Я _
ФН ( Щ И Г Е R A Д Ы ~ @ S Л Я Ж ^ C Ш М Б Q П Т Х Ю Ъ Р } \ _ # * Н У Щ D + Е R = Д Ц Й Ч [ В Ь ) O & { М Б Q П Т Х Ю Ъ Р } \ _ <
ЛН ( Щ И ] Е R % Д Ы ~ @ G / Я Э З " Ш М Б Q П Т Х Ю Ъ Р } \ _ W
ФН У Щ D К Е R A Д Ц Й Ч S + Ь Ж ^ C { М Б Q П Т Х Ю Ъ Р } \ _ V
Шифрование проводится так же, как и при простой подстановке, с той лишь разницей, что после шифрования каждого символа соответствующий ему столбец алфавитов циклически сдвигается вверх на одну позицию. Таким образом, столбцы алфавитов как бы образуют независимые друг от друга кольца, поворачиваемые вверх на один знак каждый раз после шифрования соответствующего знака исходного текста.
4.1.2.3 Многоалфавитная многоконтурная подстановка Многоконтурная подстановка заключается в том, что для шифрования ис-
пользуются несколько наборов (контуров) алфавитов, используемых циклически, причем каждый контур в общем случае имеет свой индивидуальный период применения. Частным случаем многоконтурной полиалфавитной подстановки является замена по таблице Вижинера, если для шифрования используется несколько ключей, каждый из которых имеет свой период применения.
Общая модель шифрования подстановкой может быть представлена в следующем виде:
tш = tо + w mod (k-1),
92
где tш - символ зашифрованного текста, tо - символ исходного текста,
w - целое число в диапазоне 0 - (k-1),
k - число символов используемого алфавита.
Если w фиксировано, то формула описывает одноалфавитную подстановку, если w выбирается из последовательности w1 ,w2 ,...,wn, то получается многоалфавитная подстановка с периодом n.
Если в многоалфавитной подстановке n > m (где m - число знаков шифруемого текста) и любая последовательность wi, i=1,2,...,n используется только один раз, то такой шифр является теоретически нераскрываемым. Такой шифр получил название шифра Вермэна.
Стойкость простой многоалфавитной подстановки оценивается величиной 20*n, где n - число различных алфавитов, используемых для замены. Усложнение многоалфавитной подстановки существенно повышает ее стойкость. Монофоническая подстановка может быть весьма стойкой (и даже теоретически нераскрываемой), однако строго монофоническую подстановку реализовать на практике трудно, а любые отклонения от монофоничности снижают реальную стойкость шифра.
4.2 Шифрование методом перестановки
При шифровании перестановкой символы шифруемого текста переставляются по определенному правилу в пределах блока этого текста.
Правила перестановки букв в сообщении задают шифрующие таблицы. В качестве ключа в шифрующих таблицах используются:
размер таблицы;
слово или фраза, задающие перестановку;
особенности структуры таблицы.
4.2.1 Шифрование методом простой перестановки
Одним из самых примитивных табличных шифров перестановки является простая перестановка, для которой ключом служит размер таблицы.
Пример1. Требуется зашифровать методом простой перестановки сообщение:
93

ТЕРМИНАТОР ПРИБЫВАЕТ СЕДЬМОГО В ПОЛНОЧЬ
Решение. Сообщение записывается в таблицу поочерёдно по столбцам,а считывание производится по строкам (рисунок 4.5) .
Т |
Н |
П |
В |
Е |
Г |
Л |
Е |
А |
Р |
А |
Д |
О |
Н |
Р |
Т |
И |
Е |
Ь |
В |
О |
М |
О |
Б |
Т |
М |
П |
Ч |
И |
Р |
Ы |
С |
О |
О |
Ь |
Рисунок 4.5-Шифрующая таблица для шифра простой перестановки Шифртекст записывается группами по пять букв:
ТНПВЕ ГЛЕАР АДОНР ТИЕЬВ ОМОБТ МПЧИР ЫСООЬ
Отправитель и получатель сообщения должны заранее условиться об общем ключе в виде размера таблицы. Объединение букв шифртекста в 5- буквенные группы не входит в ключ шифра и осуществляется для удобства записи несмыслового текста. При расшифровании действия выполняют в обратном порядке. Несколько большей стойкостью к раскрытию обладает метод шифрования, называемый одиночной перестановкой по ключу. Этот метод отличается от предыдущего тем, что столбцы таблицы переставляются по ключевому слову, фразе или набору чисел длиной в строку таблицы.
4.2.2 Шифрование методом простой перестановки по ключу Пример 2.Зашифровать сообщение примера1методом одиночной перестановки по ключу. В качестве ключа использовать слово П Е Л И К А Н.
Решение. Составим две таблицы, заполненные текстом сообщения и ключевым словом. На рисунке 4.6 представлена таблица до перестановки, а на рисунке 4.7 – после перестановки.
Ключ |
|
|
|
|
|
|
|
П |
Е |
Л |
И |
К |
А |
Н |
|
|
7 |
2 |
5 |
3 |
4 |
1 |
6 |
|
Т |
Н |
П |
В |
Е |
Г |
Л |
|
Е |
А |
Р |
А |
Д |
О |
Н |
|
Р |
Т |
И |
Е |
Ь |
В |
О |
|
М |
О |
Б |
Т |
М |
П |
Ч |
|
И |
Р |
Ы |
С |
О |
О |
Ь |
Рисунок 4.6 – Шифрующая таблица до перестановки
94
А |
Е |
И |
К |
Л |
Н |
П |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
Г |
Н |
В |
Е |
П |
Л |
Т |
О |
А |
А |
Д |
Р |
Н |
Е |
В |
Т |
Е |
Ь |
И |
О |
Р |
П |
О |
Т |
М |
Б |
Ч |
М |
О |
Р |
С |
О |
Ы |
Ь |
И |
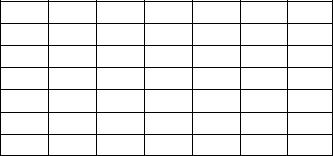
Рисунок 4.7 – Шифрующая таблица после перестановки
В верхней строке верхней таблицы записан ключ, а номера под буквами ключа определены в соответствии с естественным порядком соответствующих букв ключа в алфавите. Если бы в ключе встретились одинаковые буквы, они бы были пронумерованы слева направо. В нижней таблице столбцы переставлены в соответствии с упорядоченными номерами букв ключа.
При считывании содержимого нижней таблицы по строкам и записи шифртекста группами по пять букв получим шифрованное сообщение:
ГНВЕП ЛТООА ДРНЕР ТЕЬИО РПОТМ БЧМОР СОЫЬИ
Для обеспечения дополнительной скрытности можно повторно зашифровать сообщение, которое уже прошло шифрование. Такой метод шифрования называется двойной перестановкой. В случае двойной перестановки столбцов и строк таблицы перестановки определяются отдельно для столбцов и отдельно для строк. Сначала в таблицу записывается текст сообщения, потом поочередно переставляются столбцы, а затем строки. При расшифровании порядок перестановок должен быть обратным.
4.2.3 Шифрование методом двойной перестановки Пример 3.Зашифровать методом двойной перестановки сообщение:
П РИ Л Е Т А Ю В О С Ь М О Г О
Для шифрования использовать ключи:
по столбцам- 4 1 3 2, по строкам- 3 1 4 2
95
