
Tarasov
.pdf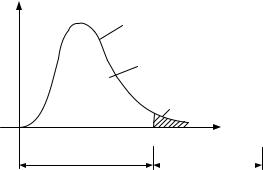
Тогда, если найденное по статистическому ряду значение χ 2 будет больше критического кр2 (α,r), то при заданном уровне значимости
гипотезу Н0 отвергают. Если же найденное значение χ 2 меньше критического, то нет оснований, чтобы отвергнуть нулевую гипотезу.
На рис.3.6 показано нахождение критической точки χкр2 (α,r) и построение критической области для критерия χ 2 .
f(x) |
Плотность распределения |
|
χ2 с r степенями свободы |
||
|
Незакрашенная |
|
|
площадь равна 1-α |
|
|
|
Закрашенная |
|
|
площадь равна α |
|
|
x |
0 |
χкр2 (α,r) |
|
|
не опровергать |
опровергнуть |
Рис.3.6
Таблица значений χкр2 (α,r) для различных α и r приведена в
приложении (табл. 4). Это таблица с двумя входами, где α значение вероятности и r – число степеней свободы. Числа, стоящие в таблице, представляют собой соответствующие значения χ 2 . Таблицу значений χ 2 можно использовать двояко.
Во-первых будем исходить из того, что величина Х действительно распределена по закону F(x). Тогда вероятность α, определенная по таблице при полученных значениях r и χ2 , есть вероятность того, что за счет чисто случайных причин мера расхождения χ 2 (3.3) будет не меньше, чем фактическое значение χ 2 в данной серии опытов.
Если эта вероятность мала, то результат опыта следует считать противоречащим гипотезе Н0 .
Напротив, если вероятность α сравнительно велика, можно признать расхождения между теоретическим и статистическим распределениями несущественными и отнести их за счет случайных причин. Тогда гипотезу Н0 можно считать правдоподобной или не противоречащей опытным данным.
Во-вторых, по заданному уровню значимости (α=0,05, α=0,1) и числу степеней свободы r из статистического ряда находят по таблице
χкр2 (α,r). Если значение χ2 (3.13) не превышает χкр2 (α,r), то говорят, что
мы не опровергаем Н0 на заданном уровне α.
На практике при использовании критерия χ 2 должно быть достаточно большим не только общее число опытов n, но и числа
наблюдений mi в отдельных разрядах (не менее 5 -10 наблюдений). Если числа наблюдений в отдельных разрядах малы (1 -2), имеет смысл их объединить.
Пример 3.2. Рассмотрим сказанное выше на данных из примера 3 .1. Вычислим вначале значение критерия χ 2 для статистического ряда, представленного таблицей 3.2. При этом три последних разряда объединены в один. Выкладки для вычисления критерия показаны в табл.3.4.
Табл.3.4
|
Интервал |
|
|
|
ˆ |
|
ˆ |
|
|
|
|
|
(m np )2 |
|
||
|
|
|
|
|
|
|
|
|
|
i |
i |
|
||||
i |
[хi , xi + 1 ) |
|
mi |
e |
λxi |
e |
λxi |
1 |
pi |
npi |
|
|
|
|
|
|
|
|
npi |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1 |
[0; 0,1) |
|
41 |
1,0 |
0,752 |
|
0,248 |
49,35 |
|
1,41 |
|
|
|
|||
2 |
[0,1; 0,2) |
|
34 |
0,752 |
0,566 |
|
0,186 |
37,01 |
|
0,24 |
|
|
|
|||
3 |
[0,2; 0,3) |
|
30 |
0,566 |
0,425 |
|
0,141 |
28,06 |
|
0,13 |
|
|
|
|||
4 |
[0,3; 0,4) |
|
20 |
0,425 |
0,320 |
|
0,105 |
20,89 |
|
0,04 |
|
|
|
|||
5 |
[0,4; 0,5) |
|
19 |
0,320 |
0,241 |
|
0,079 |
15,72 |
|
0,68 |
|
|
|
|||
6 |
[0,5; 0,6) |
|
18 |
0,241 |
0,181 |
|
0,060 |
11,94 |
|
3,08 |
|
|
|
|||
7 |
[0,6; 0,7) |
|
11 |
0,181 |
0,136 |
|
0,045 |
8,96 |
|
0,46 |
|
|
|
|||
8 |
[0,7; 0,8) |
|
9 |
0,136 |
0,102 |
|
0,034 |
6,77 |
|
0,73 |
|
|
|
|||
9 |
[0,8; 0,9) |
|
5 |
0,102 |
0,077 |
|
0,025 |
4,98 |
|
0,00 |
|
|
|
|||
10 |
[0,9; 1,0) |
|
5 |
0,077 |
0,058 |
|
0,019 |
3,78 |
|
0,39 |
|
|
|
|||
11 |
[1,0; ∞) |
|
7 |
0,058 |
0 |
|
|
0,058 |
11,54 |
|
1,79 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
χ2 =8,95 |
|
|
|
|
Из таблицы значений χ 2 (приложение табл.4) находим для r=9: |
||||||||||||||||
при χ2 =10,66 |
α=0,30; |
|
|
|
|
|
|
|
|
|
|
|
||||
при χ2 =8,34 |
α=0,50. |
|
|
|
|
|
|
|
|
|
|
|
||||
Следовательно, |
искомая вероятность α при χ 2 =8,95 |
|
приближенно |
|||||||||||||
равна 0,44. Эта вероятность малой не является и поэтому гипотезу об экспоненциальном законе распределения интервалов времени между поступлениями требований можно считать правдоподобной.
С другой стороны зададимся уровнем значимости α=0,05. По
таблице χ2 при α=0,05 и r =9 находим |
2 |
(0,05; 9) 16,92. Так как |
|
кр |
|
8,95<16,92, то можно говорить, что при уровне значимости 0,05, гипотезу об экспоненциальном распределении не отвергаем. Итак, величина критерия не дает нам оснований считать, что экспоненциальное распределение с плотностью
2,849e 2,849x , |
x 0; |
плохо согласуется с данными табл. 3.1 |
f (x) |
x 0 |
|
0, |
|
Другой подход к определению значения критерия χ 2 называется равновероятным подходом. В этом случае устраняется некоторая неоднозначность в выборе длины разрядов в статистическом ряде и

длины разрядов выбирают так, чтобы выполнялось условие: р1 =р2 =…=рk . Тогда критерий χ2 является приближенно достоверным, если k≥3 и npi ≥5 для всех i.
Например, если для вышеприведенного примера сформировать k=20
интервалов с рi =1/20=0,05, то n∙рi =199∙0,05=9,95. |
|
|
|||||
Границы |
разрядов |
хi можно |
определить |
по |
формуле |
||
xi =−0,351ln(1−i/20) для |
i=1,2,…, |
20, |
что эквивалентно |
условию |
|||
ˆ |
ˆ |
1 e |
x / 0,351 |
|
|
|
|
F (xi ) i / 20 , |
где F(x) |
|
для х≥0. При этом х0 |
=0, х2 0 |
=∞. |
||
Определение значения критерия χ 2 по равновероятному подходу и сравнение его с предыдущим значением, проделать самостоятельно.
Рассмотрим еще один критерий согласия – критерий Колмогорова - Смирнова. В отличие от критерия «хи -квадрат» критерий Колмогорова – Смирнова позволяет сравнить ста тистическую функцию
распределения Fn (x) c функцией предполагаемого распределения ˆ .
F (x)
Для этого критерия не нужно каким – либо образом группировать данные и следовательно, нет сложности с определением границ разрядов. Однако у него есть свои недостатки.
Во – первых, область его применения более ограниченна, чем у критерия «хи - квадрат», т.к. нет готовых критических значений для работы с дискретными данными. Во – вторых, исходная форма критерия достоверна только в том случае, если известн ы все параметры предполагаемого закона. Если же использовать вместо параметров их оценки по данным, то критерий может давать завышенные значения вероятности, чем точно установленные.
Для определения меры расхождения (статистики), лежащей в основе критерия Колмогорова – Смирнова, мы будем использовать
статистическую |
|
функцию |
распределения |
|
F (x) |
количество |
Х i x |
p ( X x) |
|
n |
n |
|
|
|
|
|
|
|
|
и подобранную функцию распределения ˆ . Тогда статистика этого
F (x)
критерия Dn – это наибольшее
ˆ для всех значений х: n
F (x) D
(вертикальное) расстояние между Fn (x) и
ˆ max | Fn (x) F(x) |.
А.Н.Колмогоров доказал, что какова бы ни была функция распределения
ˆ непрерывной случайной величины Х, при неограниченном
F (x)
возрастании числа независимых наблюдений n вероятность неравенства 
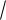 nDn λ стремится к пределу
nDn λ стремится к пределу
P(λ) 1 |
|
( 1)k e 2k |
2 |
λ |
2 |
|
|
|
. |
(3.14) |
|||
|
k |
|
|
|
|
|
Значения вероятности |
Р(λ), подсчитанные по |
формуле (3 .14) |
||||
приведены в табл. 3 .5
Табл.3.5 |
|
|
|
|
|
|
|
λ |
Р(λ) |
λ |
Р(λ) |
λ |
Р(λ) |
λ |
Р(λ) |
0,0 |
1,000 |
0,5 |
0,964 |
1,0 |
0,270 |
1,5 |
0,022 |
0,1 |
1,000 |
0,6 |
0,864 |
1,1 |
0,178 |
1,6 |
0,012 |
0,2 |
1,000 |
0,7 |
0,711 |
1,2 |
0,112 |
1,7 |
0,006 |
0,3 |
1,000 |
0,8 |
0,544 |
1,3 |
0,068 |
1,8 |
0,003 |
0,4 |
0,997 |
0,9 |
0,393 |
1,4 |
0,040 |
1,9 |
0,002 |
|
|
|
|
|
|
2,0 |
0,001 |
Схема применения критерия следующая: |
|
|
|
||||||
1) |
строятся |
статистическая |
функция |
распределения |
Fn (x) и |
||||
предполагаемая |
теоретическая |
функция |
распределения |
|
ˆ |
||||
|
F (x) и |
||||||||
определяется максимум м одуля разности между ними (рис.3 |
.7); |
||||||||
|
|
λ |
|
|
|
|
|
|
|
2) |
определяется величина |
|
n Dn и |
по таблице 3.5 |
|
находится |
|||
вероятность Р(λ). Если вероятность Р(λ) весьма мала, то гипотезу Н0 отвергают; при сравнительно больших Р(λ) гипотезу Н0 считают совместимой с опытными данными.
Пример 3.3. Применим критерий Колмогорова – Смирнова к данным статистической совокупности из табл.3.1. На рис.3 .7 приведен график разности между функциями распределения для данных об интервалах времени между поступл ениями требований и подобранного
ˆ |
e |
x / 0,351 |
. |
экспоненциального распределения F(x) 1 |
|
ˆ F (x) F(x) n
0,05
0,00
x
-0,05
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
1,0 |
1,1 |
1,2 |
|
|
|
|
Рис.3.7 |
|
|
|
|
|
|
|
Максимальная разность между двумя функциями Fn (x) и ˆ в
F (x)
точке хi =0,35 составляет −0,083. Тогда Dn =0,083 и λ=1,171. По табл . 3.5 находим Р(1,1)=0,178 и Р(1,2)=0,112. Следовательно, как и в случае применения критерия «хи – квадрат», гипотезу Н0 – об экспоненциальном распределении данных на уровне Р=0,14 мы не опровергаем. В качестве замечания отметим тот факт, ч то с ростом n прямо пропорционально растет и объем вычислений для статистики Dn .
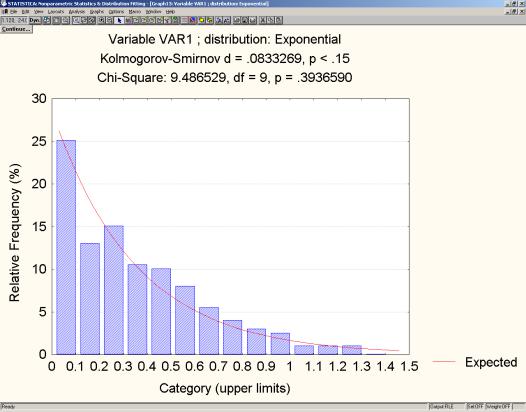
Для сравнения ниже приведены результаты расчетов по программе «Statistica» (рис.3.8, 3.9). Результаты ручного счета и программы «Statistica» – для статистики Колмогорова - Смирнова совпадают. Расхождения по критерию «хи - квадрат» объясняются тем, что в программе «Statistica» при вычислении статистики χ 2 разряды берутся другие, а именно (αi , αi + 1 ] вместо [αi , αi + 1 ) при ручном счете. Следовательно, в программе « Statistica» статистическая функция распределения Fn (x) непрерывна «справа», а не «слева», как мы допускали в п.3.2.
Это важно, особенно в тех случаях, когда данные в статистической совокупности могут повторяться, как в рассматриваемом нами примере.
Рис. 3.8

Рис. 3.9
Далее в качестве модели теоретического распределения для данных статистической совокупности из таблицы 3.1 вместо экспоненциального распределения рассмотрим гамма – распределение (см. п. 3 .5.5). Ниже на рисунках 3.10, 3.11, 3 .12 приведены расчеты по программе
«Statistica».
Рис. 3.10

Рис. 3.11
Рис. 3.12
Результаты расчета показывают, что данные статистической совокупности не противоречат и гипотезе о гамма – распределении с параметром формы α=3,87 и масштабным параметром β=1,36. При этом статистика критерия Колмогорова – Смирнова Dn =0,072 вместо 0,083 в предыдущем случае (что лучше, так как вероятность равна 0,26), а статистика критерия «хи – квадрат» − χ2 =11,85 вместо 9,49 (что хуже, так как вероятность стала 0,158 вместо 0,394).
Учитывая, что экспоненциальное распределение содержит один параметр, а гамма – распределение – два параметра, то для дальнейшего моделирования удобнее пользоваться экспоненциальным распределением.
3.6 Статистические оценки для неизвестных параметров распределения
Определив при решении первой задачи математической статистики один или несколько законов распределений, мы должны задать значения их параметров, чтобы распределения были полностью определены и могли применяться при дальнейшем моделировании. При выдвижении гипотезы о виде распределения использовались независимые и одинаково распределенные опытные данные Х1 , Х2 , …, Хn , и эти же данные будем использовать, чтобы получить оценки параметров, входящих в выбранное распределение. В таком случае говорят, что оценивают неизвестный параметр по данным статистической совокупности (выборки ). Например, если уже установлено, что закон распределения случайной величины Х нормальный, то необходимо оценить параметры m и σ. Или же, если величина распределена по закону Пуассона, то подлежит определению только один его параметр − математическое ожидание М(Х)=λ.
Рассмотрим следующую общую задачу. Имеется случ айная величина Х, закон распределения которой содержит неизвестный
параметр θ. Обозначим ˆ оценку параметра θ, причем оценка является
θ
числовой функцией величин Х1 ,Х2 ,…,Хn и следовательно, сама является
величиной случайной. Закон распределения ˆ зависит от закона
θ
распределения величины Х, от самого неизвестного параметра θ и числа опытов n.
Предъявим к оценке ˆ ряд требований по «качеству».
θ
1. Несмещенной называют статическую оценку ˆ , математическое
θ
ожидание которой равно оцениваемому параметру θ, т.е.
ˆ M (θ) θ.
В этом случае исключается систематическая ошибка в сторону завышения или занижения.

2. Оценка ˆ при увеличении числа опытов n должна сходиться по
θ
вероятности к оцениваемому параметру θ. Оценка, обладающая этим свойством, называется состоятельной.
3. Эффективной называют статическую оценку, которая по сравнению с другими имеет наименьшую дисперсию, т.е.
ˆ
D(θ) min .
Рассмотрим два типа оценок − это оценки по методу моментов (К.
Пирсона) и оценки максимального правдоподобия (Р. Фишера).
Согласно методу моментов, неизвестные параметры распределения выбираются с таким расчетом, чтобы несколько моментов теоретического распределения были равны соответствующим статическим моментам, вычисленным для данной статистической совокупности.
Пример 3.4. По данным статистической совокупности Х1 ,Х2 ,…,Хn найти методом моментов оценку неизвестного параметра λ
экспоненциального распределения с функцией плотности f (x) λe λx
(x 0).
Решение. Приравняем начальный теоретический момент первого порядка начальному статическому моменту п ервого порядка: m1 =m1 (n).
Учитывая, что m1 =M(X), m1 (n) X (n), получим M ( X ) X (n) . Так как для экспоненциального закона M ( X ) 1/ λ, то оценкой для параметра
λбудет λ 1/ X (n).
Пример 3.5. По данным статической совокупности Х1 ,Х2 ,…,Хn найти методом моментов оценки неизвестных параметров m и σ нормального распределения с функцией плотности
φ |
|
(x) |
1 |
|
|
e-( x-m) |
2 |
/(2σ |
2 |
) . |
||
m,σ |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
σ 2π |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
||||
Решение. Приравняем начальные теоретические и статические |
||||||||||||
моменты первого порядка, а также |
центральные и статистические |
|||||||||||
|
|
|
|
|
|
|
o |
|
o |
|
|
|
моменты второго порядка: m1 =m1 (n), |
m2 |
m2 (n) . Учитывая, что m1 =m, |
||||||||||
o
m2 σ2 , получим
mˆ X (n), σˆ 
 DX (n) .
DX (n) .
Замечание. Результаты примера 3 .2 мы уже использовали в п. 3.4. Рассмотрим теперь оценки максимального правдоподобия.
Допустим, что вид функции плотности f(x) для независимых и одинаково распределенных данных Х1 ,Х2 ,…,Хn установлен, но неизвестен параметр этого распределения θ.
Функцией правдоподобия для непрерывной случайной величины Х называют функцию

L(Х1 ,Х2 ,…,Хn ; θ)=f(Х1 , θ) f(Х2 , θ)… f(Хn , θ).
В качестве оценки параметра θ принимают такое его значение ˆ , при
θ
котором функция L достигает максимума. Функции L и lnL достигают максимума в одной и той же точке, поэтому ищут (что удобнее) максимум функции lnL.
Пример 3.6. Для экспоненциального распределения θ=λ (λ>0).
Составим |
логарифмическ ую |
|
|
|
функцию |
правдоподобия: |
|||||||||||||
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ln L n ln X i . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Найдем первую производную по λ: |
|
|
|
|
|||||||||||||||
|
|
|
|
|
d ln L n X i . |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
||
|
|
|
|
|
|
dλ |
|
|
|
λ |
|
|
|
i 1 |
|
||||
Так как lnL – строго возрастающая функция, то приравняв нулю |
|||||||||||||||||||
первую производную, найдем точку максимума |
|
||||||||||||||||||
|
|
ˆ |
|
|
|
|
|
n |
|
|
|
|
|
|
|
||||
|
|
n / |
X i |
1/ X (n) . |
|
||||||||||||||
|
|
λ |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
i 1 |
|
|
|
|
|
|
|
|||
Пример 3.7. Функция правдоподобия для нормального |
|||||||||||||||||||
распределения имеет вид: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
1 |
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|||
|
L |
|
|
|
|
|
|
exp( |
( X i m)2 / 2σ2 ), |
|
|||||||||
|
|
|
|
|
|
|
|
||||||||||||
|
σn ( 2π)n |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
i 1 |
|
|
|
|
|||||||
а следовательно логарифмическая функция правдоподобия |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
n |
|
||||
|
ln L n ln σ ln |
|
|
|
|
|
|
|
|
( X i m)2 /(2σ2 ) . |
|||||||||
|
( |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
2π)n |
i 1 |
|
||||||||
Найдем частные производные по m и σ:
ln L ( X i nm) / σ2 ; |
ln L n / σ ( X i m)2 |
/ σ2 . |
|||||||
|
n |
|
|
|
|
n |
|
||
m |
i 1 |
σ |
|
|
|
i 1 |
|
||
Приравняв частные производные нулю и решив полученную |
|||||||||
систему двух уравнений относительно m и σ, получим: |
|
||||||||
|
mˆ |
|
(n), |
σˆ2 D |
|
|
|
|
|
|
X |
|
|
|
. |
|
|||
|
X(n) |
|
|||||||
|
|
|
|
|
|
|
|||
Заметим, что первая оценка несмещенная, а вторая смещенная. Теперь подробнее рассмотрим тр ебования, предъявляемые к
оценкам.
3.7 Оценки для математического ожидания и дисперсии
Пусть имеется случайная величина Х с математическим ожиданием mx и дисперсией Dx и при этом обе характеристики неизвестны. В результате n независимых опытов получены результаты X1 , X2 , …, Xn . Требуется найти несмещенные и состоятельные оценки числовых характеристик mx и Dx .
В качестве оценки для mx рассмотрим среднее арифметическое
