В виде последовательного соединения двух фильтров
Каждому элементу задержки на схеме фильтра соответствует ячейка памяти цифрового устройств. Из рисунка видно, что для хранения одной переменной используется две ячейки памяти. Такое дублирование устраняется использованием одной линией задержки максимальной длины. При этом схема фильтра при M=Nпреобразуется к виду, представленному на рисунке 2.19. Это и есть каноническая форма программной реализации фильтра.
Достоинством канонической формы является меньшее количество элементов задержки, следовательно, ячеек памяти вычислительного устройства.
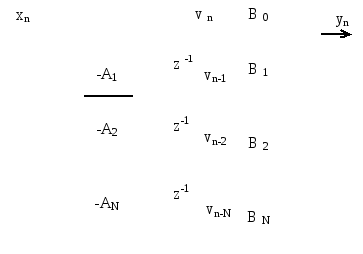
Рисунок 2.19 – Каноническая форма программной реализации фильтра
Однако обычно вместо структуры, изображенной на рисунке 2.19, используется параллельное или последовательное соединение звеньев второго порядка. Такое представление фильтра связано с возможностью представления системной функции H(z) в виде произведения или суммы системных функций с полиномами второго порядка в числителе и знаменателе
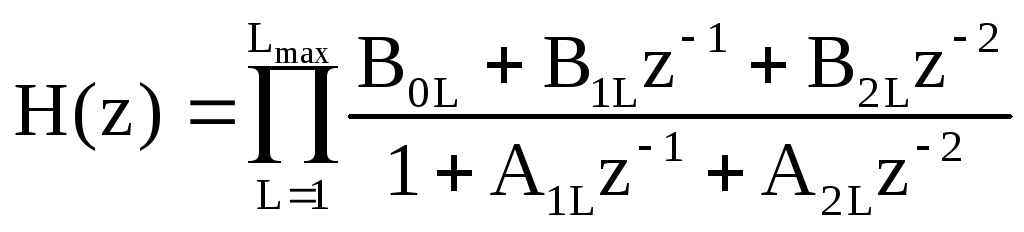 , (2.19)
, (2.19)
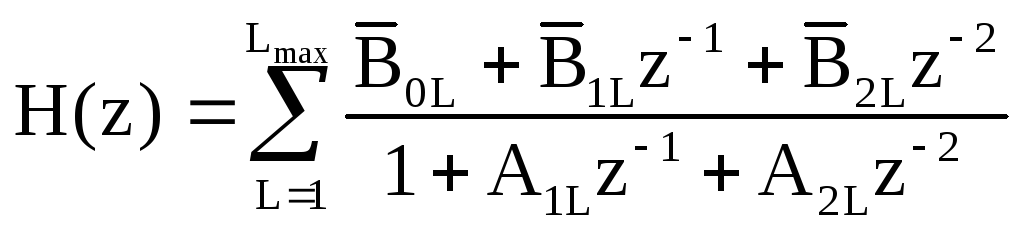 ,
(2.20)
,
(2.20)
где L– порядковый номер звена,Lmax– максимальное значение номера звена
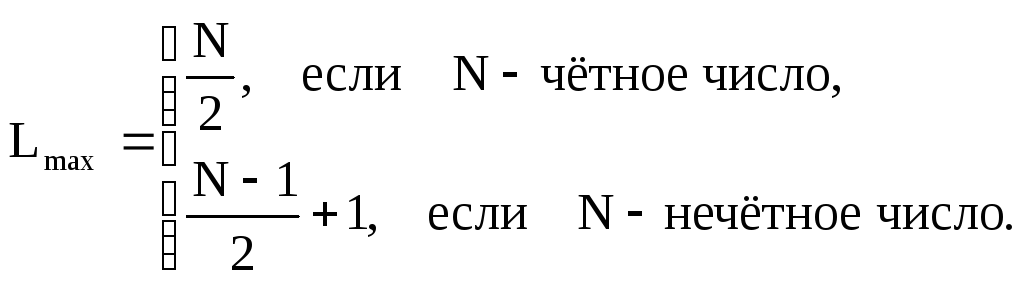
При четном Nфильтр состоит изN/2 звеньев второго порядка, при нечетномNфильтр состоит из одного звена первого порядка и (N-1)/2 звеньев второго порядка.
Системная функция звена первого порядка отличается от системной функции звена второго порядка тем, что коэффициенты B2иA2равны нулю.
Соотношению (2.19) соответствует схема рисунка 2.20 а, а соотношению (2.20) – схема рисунка 2.20 б.
Типовая схема звена второго порядка приведена на рисунке 2.21. В англоязычной литературе звено второго порядка принято называть биквадратным звеном. На входе звена показан масштабный коэффициент ML(как правило, меньше единицы), предотвращающий появление в процессе вычислений значений сигналов фильтра, выходящих за пределы разрядной сетки вычислительного устройства с фиксированной точкой.
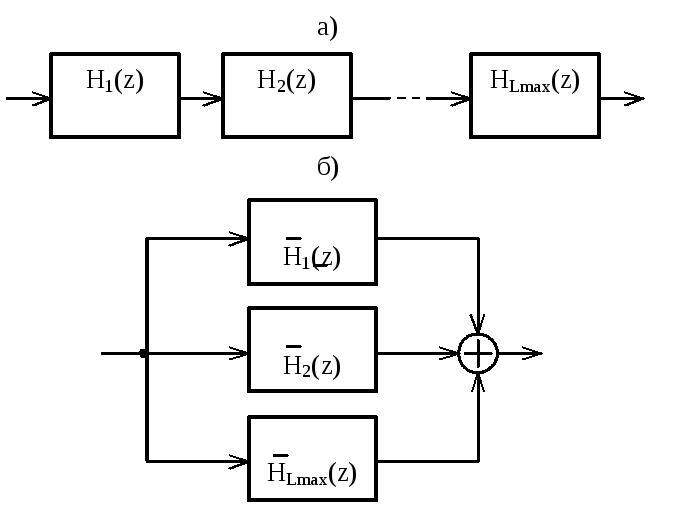
Рисунок 2.20- Последовательное (а) и параллельное (б) соединение
звеньев фильтра
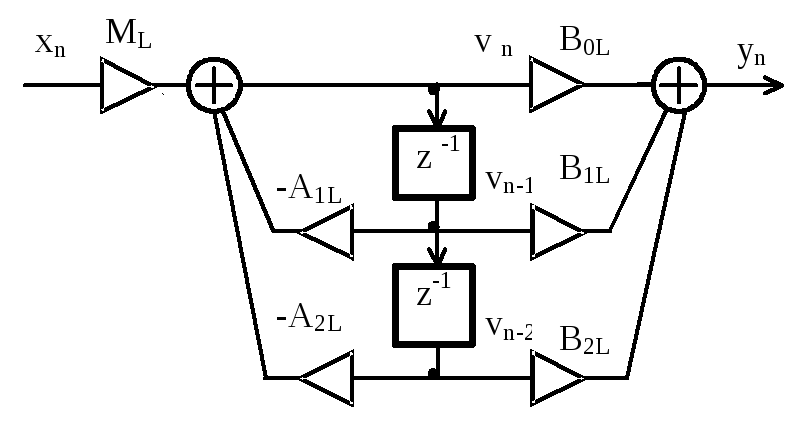
Рисунок 2.21 – Типовое звено второго порядка
2.9. Фильтры с конечной импульсной характеристикой
2.9.1. Фильтр с линейной ФЧХ
Случай 1. Симметричная импульсная характеристика, длина импульсной характеристики N– нечётное число
На рисунке 2.22 приведена симметричная импульсная характеристика конечной длины N, гдеN– нечётное число.
.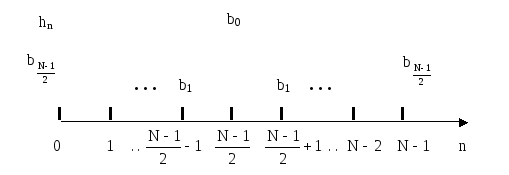
Рисунок 2.22. Симметричная импульсная характеристика КИХ – фильтра
при нечётном N
Характеристика симметрична относительно
центрального отсчёта с номером
![]()
Значение центрального отсчёта равно
![]() По
обе стороны от центрального отсчета
находится
По
обе стороны от центрального отсчета
находится![]() отсчётов со значениями
отсчётов со значениями![]()
Определим системную функцию как прямое Z– преобразование импульсной характеристики

Найдём комплексный коэффициент передачи,
используя подстановку
![]() ,
,
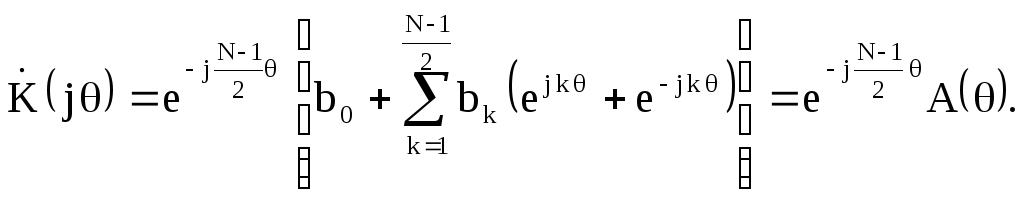 (2.21)
(2.21)
где
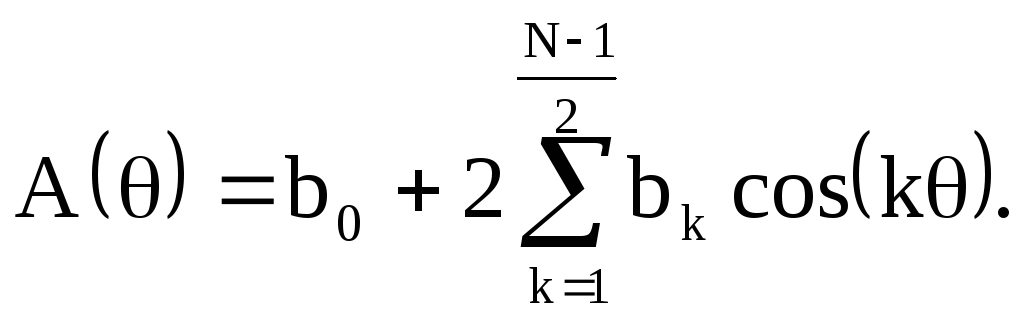
Тогда АЧХ
![]() и ФЧХ
и ФЧХ![]() при нечётномNопределятся
следующими соотношениями:
при нечётномNопределятся
следующими соотношениями:
![]() (2.22)
(2.22)
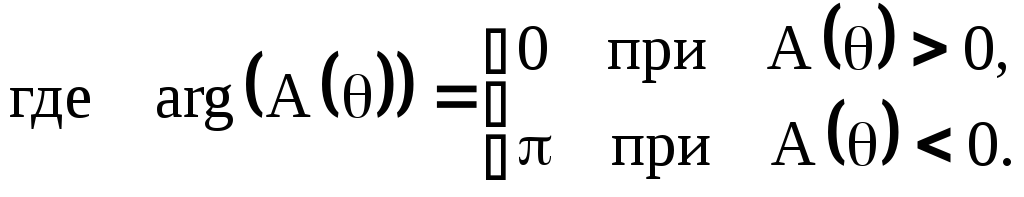
Из последнего соотношения видно, что ФЧХ фильтра линейна, а АЧХ определяется абсолютной величиной суммы ряда косинусов.
На рисунке 2.23 приведена структурная схема фильтра с линейной ФЧХ при нечетном N=5.
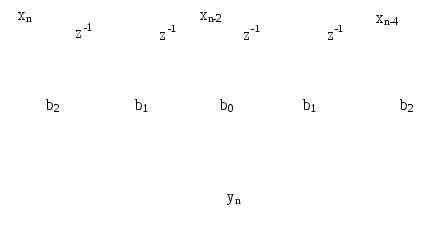
Рисунок 2.23. КИХ-фильтр с линейной ФЧХ при нечётном N=5
При длине импульсной характеристики, определяемой нечётным числом N, количество элементов задержки является чётным числомN-1, а коэффициенты системной функции симметричны относительно середины линии задержки.
Случай 2. Симметричная импульсная характеристика, длина импульсной характеристики N– чётное число
В этом случае ось симметрии проходит
между центральными отсчетами с номерами
![]() (рисунок
2.24). Определим системную функцию фильтра
(рисунок
2.24). Определим системную функцию фильтра


Рисунок 2.24. Симметричная импульсная характеристика КИХ – фильтра
при чётном N
Подставив в выражение для системной
функции
![]() ,
найдём комплексный коэффициент передачи
фильтра
,
найдём комплексный коэффициент передачи
фильтра
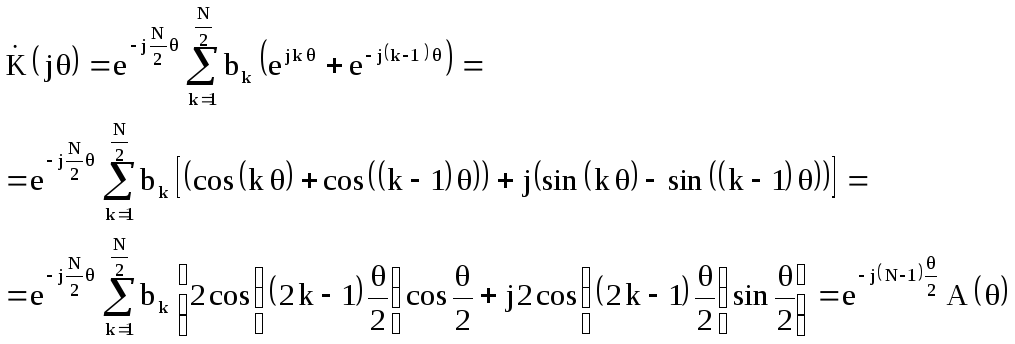 (2.23)
(2.23)
где
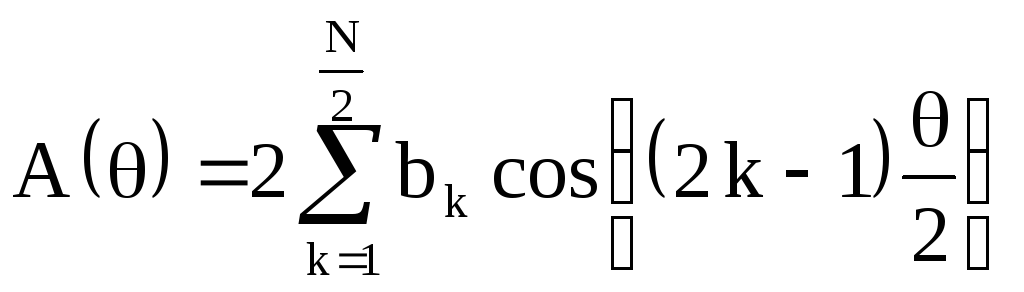 .
.
Тогда АЧХ
![]() и ФЧХ
и ФЧХ![]() при чётномNопределятся
следующими соотношениями:
при чётномNопределятся
следующими соотношениями:
![]() (2.24)
(2.24)
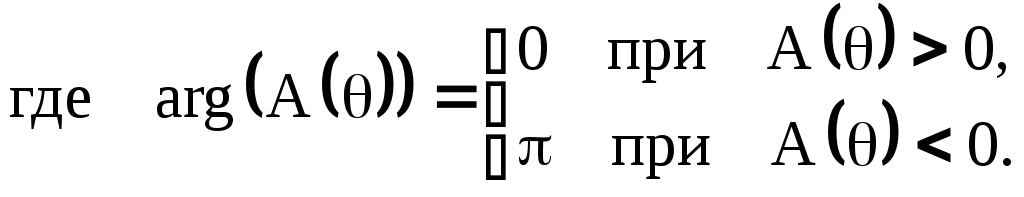
Из (2.24) видно, что ФЧХ линейна.
На рисунке 2.25 приведена структурная схема фильтра с линейной ФЧХ при четном N=4.
При длине импульсной характеристики, определяемой чётным числом N, количество элементов задержки является нечётным числомN-1, а коэффициенты системной функции симметричны относительно центрального элемента линии задержки.
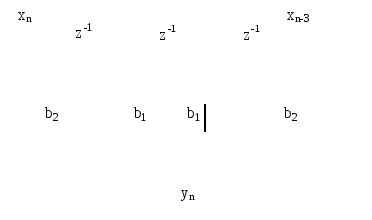
Рисунок 2.25. КИХ-фильтр с линейной ФЧХ при чётном N=4
2.9.2. Однородный фильтр
Однородным называется фильтр, у которого все отсчёты импульсной характеристики одинаковы. Для уменьшения количества операций умножения при реализации фильтра эти отсчёты принимаются равными единице, а коэффициент передачи фильтра регулируется масштабным коэффициентом на его входе. Однородный фильтр называют также фильтром скользящего среднего.
На рисунке 2.26 приведена импульсная характеристика однородного фильтра длиной N=5, а на рисунке 2.27 его структурная схема.

Рисунок 2.26. Импульсная характеристика однородного фильтра при N=5
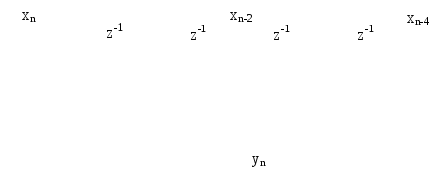
Рисунок 2.27. Однородный фильтр
Пусть требуется определить и построить графики АЧХ и ФЧХ фильтра. Решим эту задачу двумя способами.
Способ 1. Воспользуемся соотношениями (2.21) при N=5 иbk=1 дляk=0, 1, 2, 3, 4.
Тогда
![]()
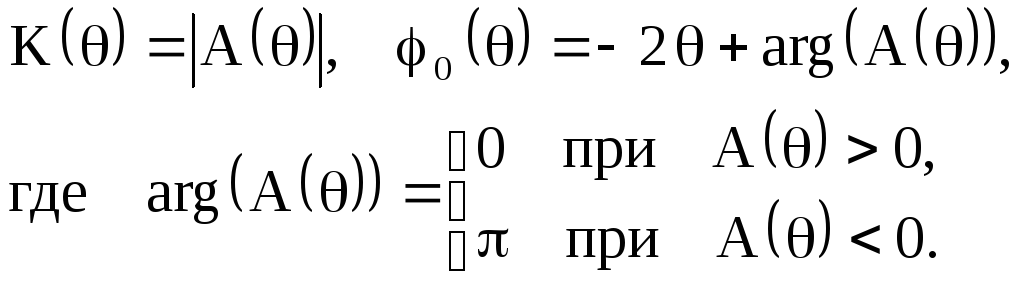 (2.25)
(2.25)
На рисунках 2.28 и 2.29 приведены АЧХ и ФЧХ однородного фильтра при N=5
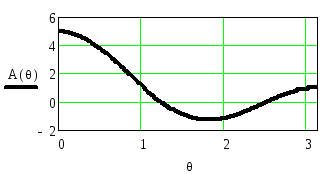
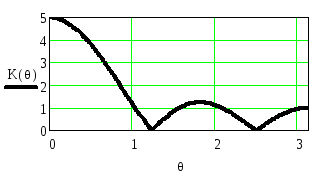
Рисунок 2.28. Функция
![]() и АЧХ однородного фильтра
и АЧХ однородного фильтра![]()

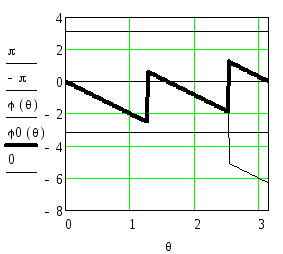
Рисунок 2.29.
ФЧХ однородного фильтра до
![]() и после
и после![]() приведения в интервал
приведения в интервал
от -![]() до
до![]()
Из АЧХ следует, что однородный фильтр является фильтром нижних частот. Особенностью АЧХ являются пульсации в полосе задерживания. Максимальный коэффициент передачи фильтра равен K(0)=5. Чтобы его уменьшить, например, до единицы, нужно использовать на входе фильтра масштабный коэффициентM=1/5, как это показано на рисунке 2.30.
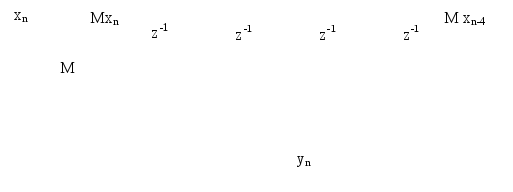
Рисунок 2.30. Однородный фильтр с масштабным коэффициентом Mна входе
На рисунке 2.29 слева сплошными линиями
представлена ФЧХ
![]() рассчитанная по (2.25), а пунктиром показаны
её составляющие
рассчитанная по (2.25), а пунктиром показаны
её составляющие![]() и
и![]() .
.
Однако общепринятым является представление
ФЧХ в интервале от
![]() до
до![]() .
Такое представление связано с
периодичностью синусоидального сигнала.
Ведь ФЧХ показывает, какой фазовый сдвиг
приобретает синусоидальный сигнал при
прохождении через фильтр, а для синусоиды
фазовый сдвиг, кратный
.
Такое представление связано с
периодичностью синусоидального сигнала.
Ведь ФЧХ показывает, какой фазовый сдвиг
приобретает синусоидальный сигнал при
прохождении через фильтр, а для синусоиды
фазовый сдвиг, кратный![]() ,
эквивалентен нулевому фазовому сдвигу.
Следовательно, ФЧХ
,
эквивалентен нулевому фазовому сдвигу.
Следовательно, ФЧХ![]() можно ввести в интервал от
можно ввести в интервал от![]() до
до![]() путем прибавления или вычитания целого
числа
путем прибавления или вычитания целого
числа![]()
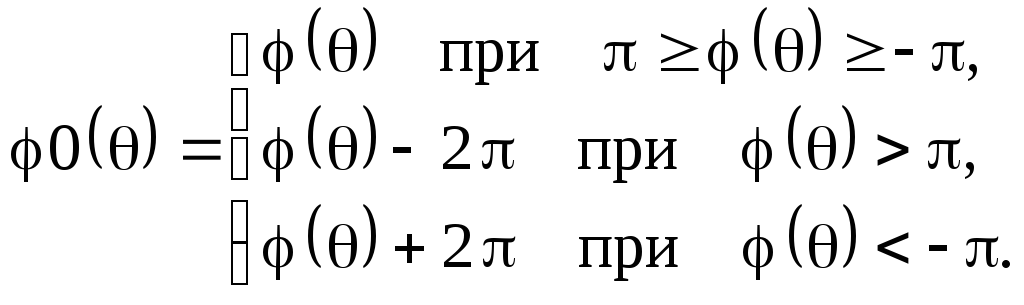 (2.26)
(2.26)
Если после выполнения (2.26)
![]() не войдёт в заданный интервал, то (2.26)
нужно выполнить повторно, предварительно
приняв
не войдёт в заданный интервал, то (2.26)
нужно выполнить повторно, предварительно
приняв![]()
В рассматриваемом случае достаточно
прибавить к
![]()
![]() в интервале значений
в интервале значений![]() ,
при которых
,
при которых![]() В результате получается ФЧХ
В результате получается ФЧХ![]() ,
приведённая на рисунке 2.29 справа. На
этом же рисунке приведена исходная ФЧХ
,
приведённая на рисунке 2.29 справа. На
этом же рисунке приведена исходная ФЧХ![]() ,
которая отличается от
,
которая отличается от![]() только на участке, где
только на участке, где![]() .
.
Способ 2. В соответствии со схемой 2.27 запишем разностное уравнение
![]()
Найдём Z-преобразование
последовательности![]()
![]()
Определим системную функцию
![]()
Используя подстановку
![]() ,
получим выражение для комплексного
коэффициента передачи
,
получим выражение для комплексного
коэффициента передачи
![]()
Из последнего соотношения получим
![]()
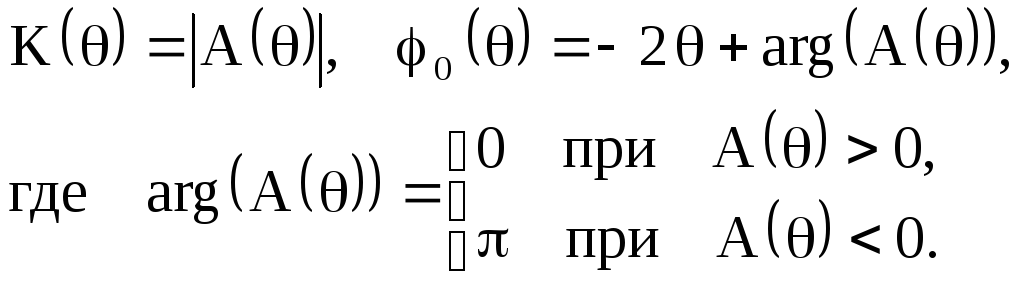
Как видно, полученные соотношения не отличаются от (2.25).
Выясним влияние длины импульсной
характеристики Nна АЧХ
и ФЧХ фильтра. Для этого выполним расчёт
АЧХ и ФЧХ приN=10. Из (2.24)
при![]() получим
получим
![]()
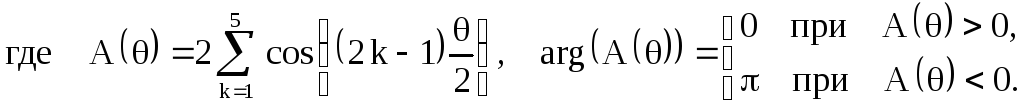
Рассчитанные по этим формулам АЧХ и ФЧХ приведены на рисунках 2.30 и 2.31. Для приведения ФЧХ в стандартный интервал соотношение (2.26) было применено дважды.
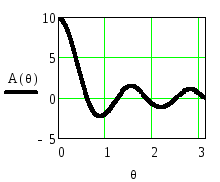
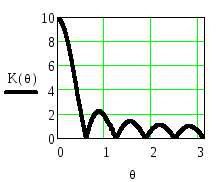
Рисунок 2.30. Функция
![]() и АЧХ однородного фильтра приN=10
и АЧХ однородного фильтра приN=10

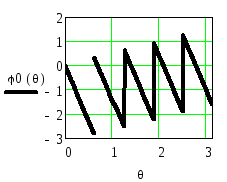
Рисунок 2.31. ФЧХ однородного фильтра при N=10 без приведения и с приведением
в интервал от
![]() до
до![]()
На рисунке 2.32 приведены АЧХ однородных фильтров с масштабными коэффициентами на входе, выбранных из условия получения максимального коэффициента передачи фильтров, равного единице, при N=5 иN=10.
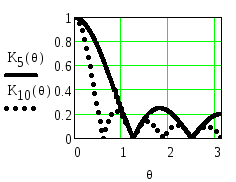
Рисунок 2.32. АЧХ однородных фильтров
при N=5 (![]() )
иN=10 (
)
иN=10 (![]()
Из рисунка видно, что увеличение длины линии задержки
сужает полосу пропускания фильтра,
увеличивает частоту пульсаций АЧХ в полосе задерживания,
уменьшает амплитуду пульсаций в полосе задерживания.
2.9.3. Триангулярный фильтр
Триангулярным называется фильтр с треугольной огибающей отсчетов импульсной характеристики (рисунок 2.33).
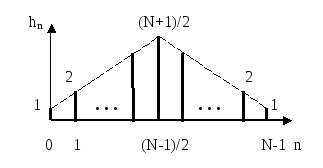
Рисунок 2.33. Импульсная характеристика триангулярного фильтра
При N=3 и минимальном значении отсчёта, равным единице, максимальный отсчёт с
номером 1 равен 2, при N=5
максимальный отсчёт равен![]()
Поскольку импульсная характеристика симметрична относительно её центрального отсчёта, то триангулярный фильтр является фильтром с линейной ФЧХ.
На рисунке показана импульсная характеристика с минимальным значением отсчёта, равным единице. В общем случае все отсчеты этой характеристики могут быть пропорционально уменьшены или увеличены.
Покажем, что треугольная импульсная характеристика триангулярного фильтра hnможет быть получена как дискретная свёртка двух одинаковых импульсных характеристикh0nоднородного фильтра
![]() (2.27
(2.27
Процесс получения отсчётов импульсной характеристики триангулярного фильтра иллюстрирует рисунок 2.32.
На рисунке приведена импульсная
характеристика однородного фильтра
![]() .
Длина импульсной характеристики равнаN0, все отсчёты равны
единице.
.
Длина импульсной характеристики равнаN0, все отсчёты равны
единице.
Из (2.27) видно, что для определения
нулевого отсчета дискретной свёртки
h0нужно отсчеты
импульсной характеристикиh0kумножить на совпадающие с ними по времени
отсчеты характеристики![]() ,
приведённой на рисунке 2.34 в позиции
«1», и выполнить суммирование
полученных произведений. Из рисунка
видно, что результатом этих операций
является
,
приведённой на рисунке 2.34 в позиции
«1», и выполнить суммирование
полученных произведений. Из рисунка
видно, что результатом этих операций
является![]()
Для определения первого отсчета
дискретной свёртки h1требуется отсчёты импульсной характеристикиh0kумножить на совпадающие с ними во времени
отсчёты характеристикиh01-k,
приведённой на рисунке 2.34 в позиции
«2», и выполнить суммирование
произведений. Из рисунка видно, что в
этой позиции перекрываются уже две пары
отсчётов, поэтому сумма произведений
будет равна![]()
Каждое смещение характеристики
![]() на один отсчёт вправо относительноh0kбудет увеличивать сумму произведений
на единицу. Для отсчёта дискретной
свёртки
на один отсчёт вправо относительноh0kбудет увеличивать сумму произведений
на единицу. Для отсчёта дискретной
свёртки![]() сумма произведений будет максимальной
и равнойN0. Этот случай
представлен позицией «3» на рисунке
2.34.
сумма произведений будет максимальной
и равнойN0. Этот случай
представлен позицией «3» на рисунке
2.34.
Дальнейшее смещение h0n-kотносительноh0kприводит к уменьшению отсчетов дискретной
свёртки. В позиции «4» показано, что
отсчёт дискретной свёртки![]() .
.
В позиции «5» определяется последний
отсчёт дискретной свёртки с номером![]() ,
равный единице.
,
равный единице.
Временная диаграмма дискретной свёртки hnимпульсных характеристикиh0nодинаковых однородных фильтров приведена на рисунке 2.35.

Рисунок 2.34. Дискретная свёртка импульсных характеристик двух одинаковых
однородных фильтров
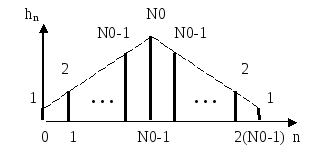
Рисунок 2.35. Временная диаграмма дискретной свёртки импульсных характеристик
двух одинаковых однородных фильтров
Сравнение рисунков 2.35 и 2.33 показывает, что временная диаграмма дискретной свёртки не отличается от импульсной характеристики триангулярного фильтра, если выполняется условие
![]()
Определим системную функцию триангулярного
фильтра
![]() ,
воспользовавшись соотношением для
дискретной свёртки (2.26) и учитывая, что
прямоеZ-преобразование
дискретной свёртки равно произведениюZ-преобразований свёртываемых
последовательностей,
,
воспользовавшись соотношением для
дискретной свёртки (2.26) и учитывая, что
прямоеZ-преобразование
дискретной свёртки равно произведениюZ-преобразований свёртываемых
последовательностей,
![]()
где
![]()
Из последнего соотношения следует связь между комплексными коэффициентами передачи триангулярного и однородного фильтров
![]() (2.28)
(2.28)
Если
![]() является нечётным числом, то подставляя
(2.21) в последнее соотношение приbk=1
и длине импульсной характеристики
однородного фильтраN0,
получим
является нечётным числом, то подставляя
(2.21) в последнее соотношение приbk=1
и длине импульсной характеристики
однородного фильтраN0,
получим
![]()
где
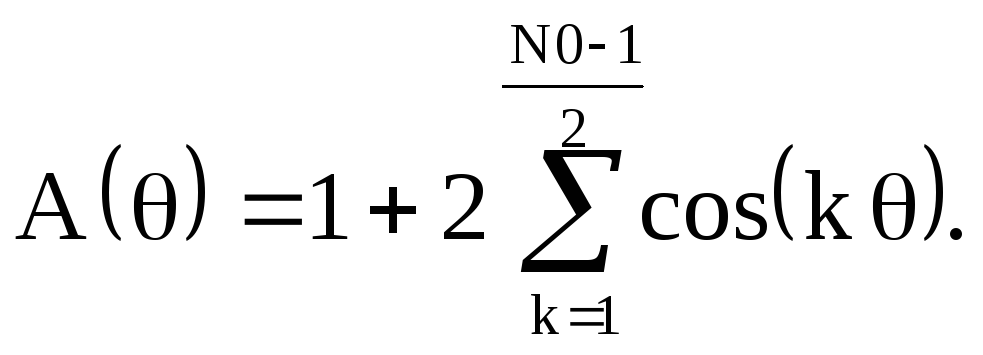
Из последнего соотношения найдём АЧХ
![]() и ФЧХ
и ФЧХ![]() без приведения в интервал от
без приведения в интервал от![]() до
до![]()
 (2.29)
(2.29)
Если
![]() является чётным числом, то подставляя
(2.23) в последнее соотношение приbk=1
и длине импульсной характеристики
однородного фильтраN0,
получим
является чётным числом, то подставляя
(2.23) в последнее соотношение приbk=1
и длине импульсной характеристики
однородного фильтраN0,
получим
![]()
где
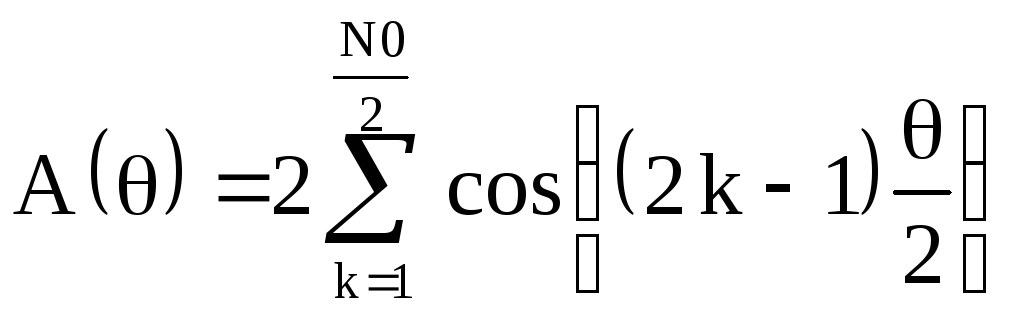 .
.
Из последнего соотношения найдём АЧХ
![]() и ФЧХ
и ФЧХ![]() без приведения в интервал от
без приведения в интервал от![]() до
до![]()
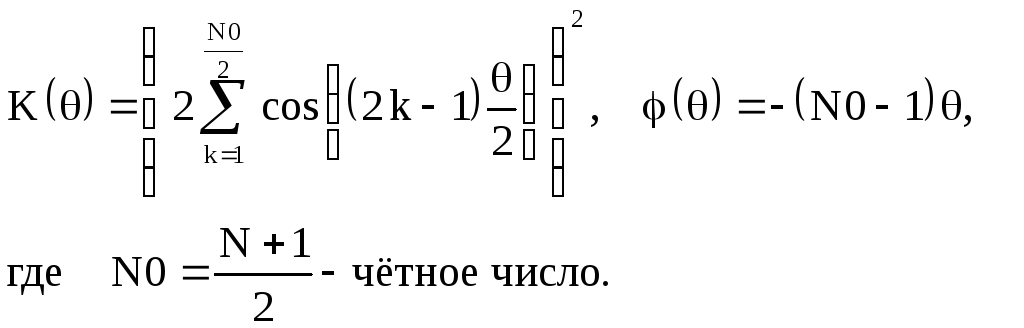 (2.30)
(2.30)
Выполним расчёт АЧХ и ФЧХ триангулярного фильтра рисунка 2.36
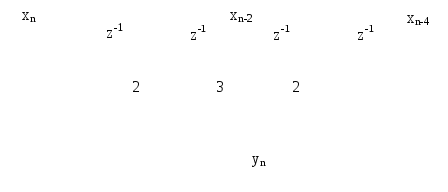
Рисунок 2.36. Триангулярный фильтр при N=5
Определим длину импульсной характеристики однородного фильтра
![]()
Поскольку N0=3 является нечётным числом расчет АЧХ и ФЧХ выполним по (2.29)
![]()
На рисунке 2.37 приведены АЧХ
![]() фильтра,
ФЧХ
фильтра,
ФЧХ![]() рассчитанная по последней формуле, и
ФЧХ
рассчитанная по последней формуле, и
ФЧХ![]() ,
приведённая в стандартный интервал
,
приведённая в стандартный интервал
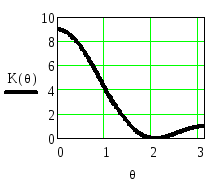
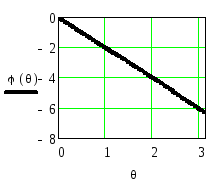
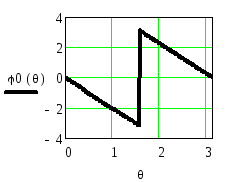
Рисунок 2.37. АЧХ и ФЧХ триангулярного фильтра при длине импульсной
характеристики N=5
Из рисунка видно, что триангулярый фильтр, как и однородный, является фильтром нижних частот.
На рисунке 2.38 приведены АЧХ триангулярного и однородного фильтров с N=5 и с одинаковыми значениями максимального коэффициента передачи за счёт соответствующего выбора масштабных коэффициентов (Mo=1/5,Mt=1/9

Рисунок 2.38. АЧХ триангулярного и однородного фильтров при N=5
Из рисунка видно, что АЧХ триангулярного фильтра имеет меньший уровень пульсаций в полосе задерживания по сравнению с АЧХ однородного фильтра, но большую ширину главного лепестка АЧХ.
2.9.4. Гребенчатый фильтр
На рисунке 2.39 приведена структурная схема гребенчатого фильтра, в состав которого входит линия задержки из N-1 элемента. Коэффициентb может принимать два значенияb=1 илиb= -1.
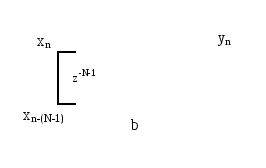
Рисунок 2.39
На рисунке 2.40 приведены две импульсные характеристики фильтра при b=1 и при
b= -1.
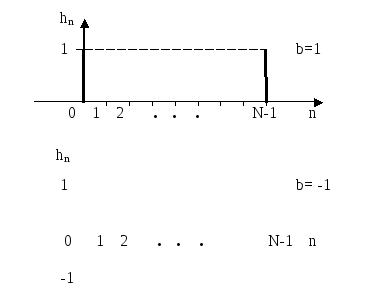
Рисунок 2.40. Импульсные характеристики гребенчатых фильтров
Определим системную функцию фильтра двумя способами:
Способ 1.
Системная функция является прямым Z-преобразованием импульсной характеристики
![]()
Способ 2.
Воспользовавшись схемой рисунка 2.39 запишем разностное уравнение
![]()
Выразим Z-преобразование выходного сигнала черезZ-преобразование входного сигнала
![]()
Определим системную функцию
![]()
Комплексный коэффициент передачи фильтра равен
![]()
Определим комплексный коэффициент передачи фильтра при b=1
![]()
где
![]()
Найдём АЧХ и ФЧХ фильтра
![]()

На рисунке 2.41 приведены функция
![]() и АЧХ
и АЧХ![]() ,
а на рисунке 2.42 – ФЧХ
,
а на рисунке 2.42 – ФЧХ![]() и ФЧХ
и ФЧХ![]() приведённая в стандартный интервал от
приведённая в стандартный интервал от![]() до
до![]() .
ФЧХ
.
ФЧХ![]() получена в результате двукратного
использования соотношения (2.26).
получена в результате двукратного
использования соотношения (2.26).
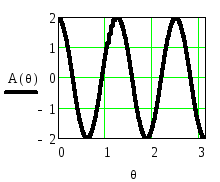
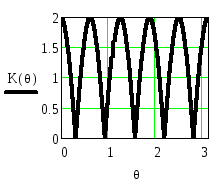
Рисунок 2.41.
Функция
![]() и АЧХ
и АЧХ![]() приb=1
приb=1
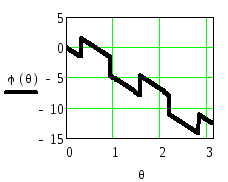

Рисунок 2.42.
ФЧХ
![]() и ФЧХ
и ФЧХ![]() приведённая в стандартный интервал
приведённая в стандартный интервал
Определим комплексный коэффициент передачи фильтра при b=-1
![]()
где
![]()
Найдём АЧХ и ФЧХ фильтра
![]()
На рисунке 2.43 приведены функция
![]() и АЧХ
и АЧХ![]() ,
а на рисунке 2.44 – ФЧХ
,
а на рисунке 2.44 – ФЧХ![]() и ФЧХ
и ФЧХ![]() приведённая в стандартный интервал от
приведённая в стандартный интервал от![]() до
до![]() .
.
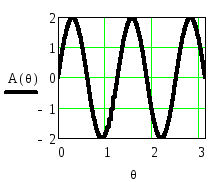
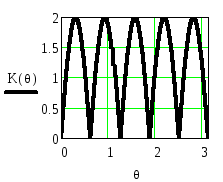
Рисунок 2.43. Функция
![]() и АЧХ
и АЧХ![]() приb= -1
приb= -1
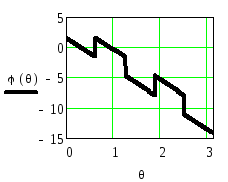
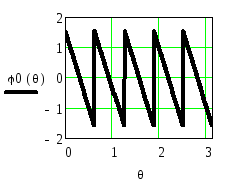
Рисунок 2.44.
ФЧХ
![]() и ФЧХ
и ФЧХ![]() приведённая в стандартный интервал
приведённая в стандартный интервал
Из рисунков видно, что АЧХ фильтра
состоит из одинаковых лепестков,
количество и ширина которых зависят от
длины импульсной характеристики.
Диапазон частот, соответствующий ширине
лепестка, равен
![]() С увеличением длины импульсной
характеристикиNширина
лепестка уменьшается, а их количество
увеличивается, и АЧХ становится похожей
на гребёнку, поэтому фильтр называется
гребенчатым.
С увеличением длины импульсной
характеристикиNширина
лепестка уменьшается, а их количество
увеличивается, и АЧХ становится похожей
на гребёнку, поэтому фильтр называется
гребенчатым.
ФЧХ фильтра является линейно-ломаной, однако, в пределах каждого лепестка она линейна как при b=1, так и приb= -1.
2.10. Рекурсивные цифровые фильтры
2.10.1. Цифровой резонатор
Цифровой резонатор (рисунок 2.45) представляет собой звено второго порядка (рисунок 2.21), у которого коэффициенты системной функции B1иB2равны нулю, а коэффициентB0=1.
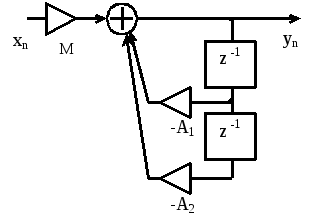
Рисунок 2.45. Цифровой резонатор
Для определения системной функции резонатора запишем разностное уравнение
![]()
Перейдём от разностного уравнения к уравнению для Z-преобразований дискретных сигналов
![]()
Из последнего уравнения выразим
![]() через
через![]()
![]()
Определим системную функцию фильтра
![]() (2.31)
(2.31)
Определим полюсы системной функции. Для этого приравняем знаменатель нулю и найдем корни полученного квадратного уравнения
![]()
![]()
 .
.
При этом системная функция преобразуется к виду
![]() (2.32)
(2.32)
В цифровом резонаторе полюсы системной функции должны быть комплексно-сопряжёнными.
Следовательно, должно выполняться условие
![]() .
.
При этом условии полюсы системной функции определяются следующим соотношением
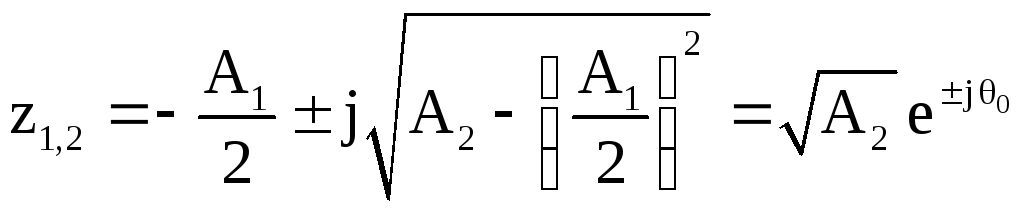 ,
(2.33)
,
(2.33)
где
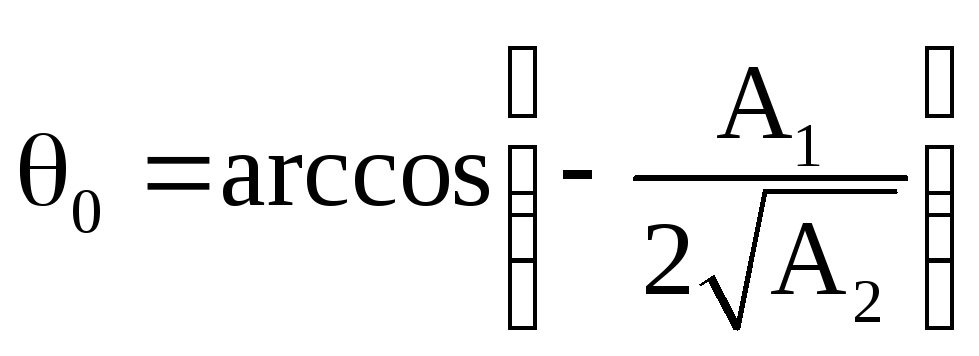 .
.
На рисунке 2.46 показаны полюсы системной функции резонатора на комплексной плоскости z. Окружность единичного радиуса с центром в начале координат является геометрическим местом точек, для которых выполняется условие
![]() .
.

Рисунок 2.46. Полюсы системной функции z1иz2
При изменении θ от 0 до π частота
![]() изменяется от 0 доFД/ 2. При этом конец вектора
изменяется от 0 доFД/ 2. При этом конец вектора![]() перемещается по окружности единичного
радиуса. Расстояние конца этого вектора
от полюса системной функции минимально
при
перемещается по окружности единичного
радиуса. Расстояние конца этого вектора
от полюса системной функции минимально
при![]() ,
т.е. при
,
т.е. при![]() ,
где
,
где![]() - резонансная частота резонатора.
- резонансная частота резонатора.
Подставляя в последнее соотношение θ0из (2.33), получим
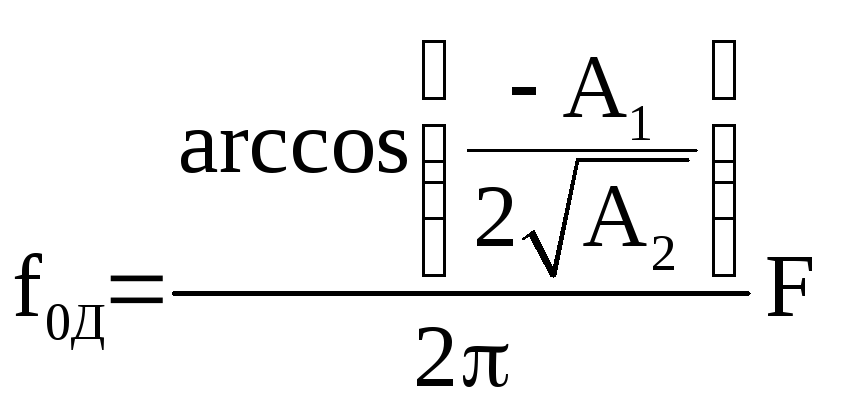 . (2.34)
. (2.34)
Из последнего соотношения видно, что резонансная частота прямо пропорциональна частоте дискретизации FДи зависит от коэффициентов системной функцииA1иA2. ПриA1=0 резонансная частота равна четверти частоты дискретизации, приA1<0 резонансная частота меньше четверти частоты дискретизации, а приA1> 0 – больше четверти частоты дискретизации.
Сначала рассмотрим частный случай
настройки резонатора на частоту, равную
четверти частоты дискретизации, при
![]() и определим комплексный коэффициент
передачи, АЧХ и ФЧХ резонатора.
и определим комплексный коэффициент
передачи, АЧХ и ФЧХ резонатора.
Подставляя в (2.31)
![]() ,
получим
,
получим
![]() .
.
Последнее соотношение позволяет определить АЧХ и ФЧХ резонатора:
![]() ,
(2.35)
,
(2.35)
 .
(2.36)
.
(2.36)
Из (2.35) видно, что на резонансной частота
при
![]() резонансный коэффициент передачи равен
резонансный коэффициент передачи равен
![]() (2.37)
(2.37)
Из этого же соотношения следует, что
![]()
Например, при M=1,A2=0.999 резонансный коэффициент передачи равен 1000, а коэффициенты передачи на границах рабочего интервала примерно равны 0.5.
На рисунке 2.47 приведена АЧХ, рассчитанная по (2.35), а на рисунке 2.48 – ФЧХ, рассчитанная по (2.36) при A2=0.9,M=1-A2.

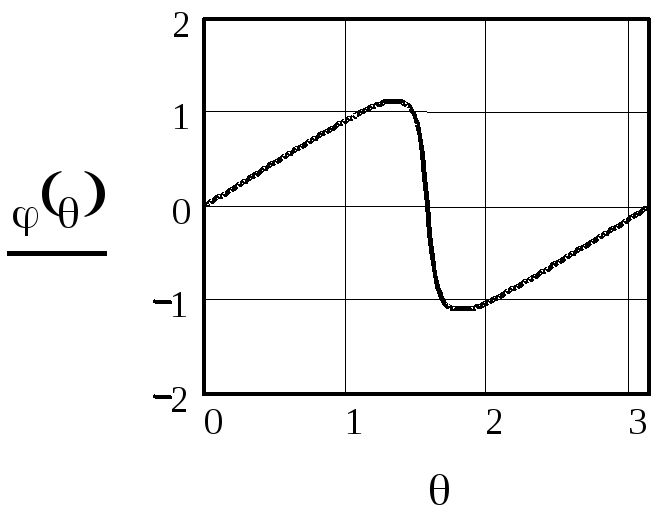
Рисунок 2.47 -АЧХ резонатора Рисунок 2.48 -ФЧХ резонатора
при
![]() =0.9,
=0.9,![]() =0,
M=1-
=0,
M=1-![]() при
при![]() =0.9,
=0.9,![]() =0
=0
Из
рисунка 2.47 видно, что АЧХ цифрового
резонатора по форме похожа на резонансную
кривую аналогового колебательного
контура. ФЧХ
резонатора (рисунок 2.48) не линейна,
фазовые сдвиги, вносимые резонатором
на частотах 0,
![]() и
и![]() ,
равны нулю. Фазовый сдвиг на частота
ниже частоты
,
равны нулю. Фазовый сдвиг на частота
ниже частоты![]() положительный, а на частотах выше
положительный, а на частотах выше![]() отрицательный.Вблизи
резонансной частоты ФЧХ цифрового
резонатора подобна ФЧХ аналогового
колебательного контура,
а при больших расстройках существенно
отличается.
отрицательный.Вблизи
резонансной частоты ФЧХ цифрового
резонатора подобна ФЧХ аналогового
колебательного контура,
а при больших расстройках существенно
отличается.
АЧХ и ФЧХ при A1=0,A2=0.99 приведены на рисунках 2.49 и 2.50 соответственно.

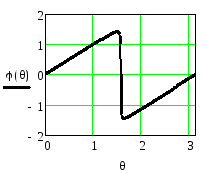
Рисунок 2.49 -АЧХ резонатора Рисунок 2.50 -ФЧХ резонатора
при
![]() =0.99,
=0.99,![]() =0,
M=1-
=0,
M=1-![]() при
при![]() =0.99,
=0.99,![]() =0
=0
Сравнение характеристик при разных значениях коэффициента А2показывает, что при стремлении А2к единице резонанс становится более острым и увеличивается крутизна ФЧХ вблизи резонансной частоты.
А теперь выясним, как влияет коэффициент A1на АЧХ и ФЧХ цифрового резонатора.
Для этого рассмотрим АЧХ и ФЧХ при А1<0 и приA1>0. Соответствующие графики приведены на рисунках 2.51 .. 2.54.
![]()
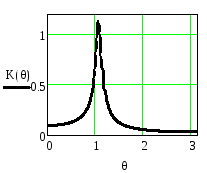
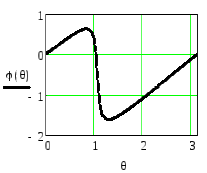
Рисунок 2.51 - АЧХ резонатора Рисунок 2.52 -ФЧХ резонатора
при
![]() =0.9,
=0.9,![]() =
-0.9, M=1-
=
-0.9, M=1-![]() при
при![]() =0.9,
=0.9,![]() =
-0.9
=
-0.9
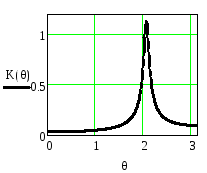
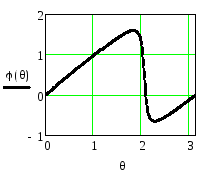
Рисунок 2.53 - AЧХ резонатора Рисунок 2.54 - ФЧХ резонатора
при
![]() =0.9,
=0.9,![]() =
0.9, M=1-
=
0.9, M=1-![]() при
при![]() =0.9,
=0.9,![]() =0.9
=0.9
Из приведенных рисунков видно, что коэффициент А1влияет на резонансную частоту резонатора. В результате АЧХ и ФЧХ сдвигаются вдоль оси частот. При этом нарушается симметрия АЧХ, становятся различными абсолютные значения максимального и минимального фазового сдвигов, вносимых резонатором, изменяется максимальное значение коэффициента передачи.
Определим комплексный коэффициент
передачи резонатора при
![]() Для этого в выражение для системной
функции (2.32) подставим
Для этого в выражение для системной
функции (2.32) подставим![]() и
и![]() из (2.33)
из (2.33)
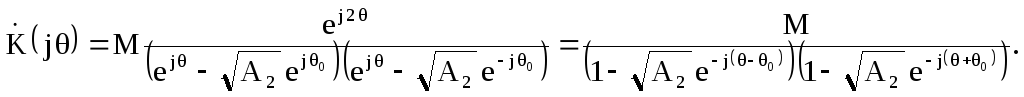 (2.38)
(2.38)
Резонансный коэффициент передачи равен
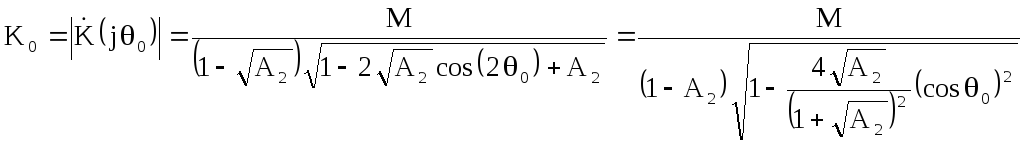 .
.
При
![]() коэффициент перед
коэффициент перед![]() в
последнем выражении равен 0.97, при
приближении А2к единице он
стремится к единице. Поэтому при
в
последнем выражении равен 0.97, при
приближении А2к единице он
стремится к единице. Поэтому при![]() ,
что, как правило, выполняется в цифровых
резонаторах, можно воспользоваться
приближённым соотношением
,
что, как правило, выполняется в цифровых
резонаторах, можно воспользоваться
приближённым соотношением
![]() (2.39)
(2.39)
Из (2.39), как частный случай при
![]() получается (2.37). Из последнего соотношения
видно, что минимум резонансного
коэффициента передачи при постоянных
значенияхMиA2имеет место при
получается (2.37). Из последнего соотношения
видно, что минимум резонансного
коэффициента передачи при постоянных
значенияхMиA2имеет место при![]() .
По мере отклонения резонансной частоты
от этого значения резонансный коэффициент
передачи увеличивается.
.
По мере отклонения резонансной частоты
от этого значения резонансный коэффициент
передачи увеличивается.
Соотношение (2.39) позволяет определить масштабный коэффициент M, обеспечивающий требуемое значение резонансного коэффициента передачи.
Определим АЧХ резонатора – зависимость модуля комплексного коэффициента передачи (2.38) от частоты
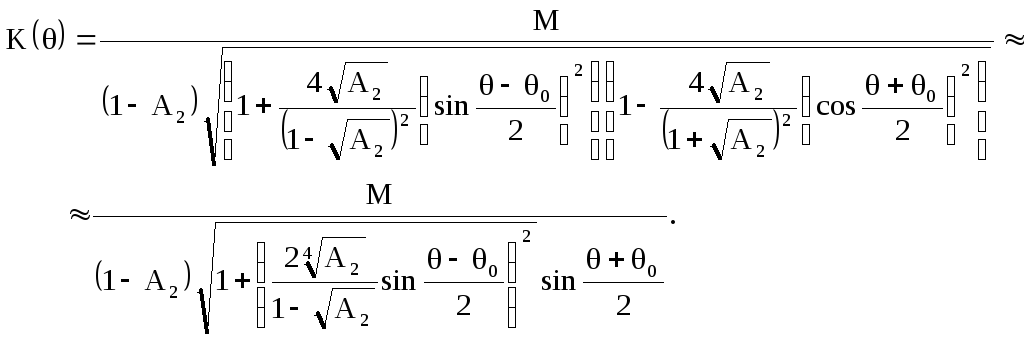
Как и (2.39) последнее соотношение
справедливо при
![]() .
.
Разделив
![]() на резонансный коэффициент передачи
на резонансный коэффициент передачи![]() ,
получим АЧХ в относительном масштабе
по оси ординат
,
получим АЧХ в относительном масштабе
по оси ординат
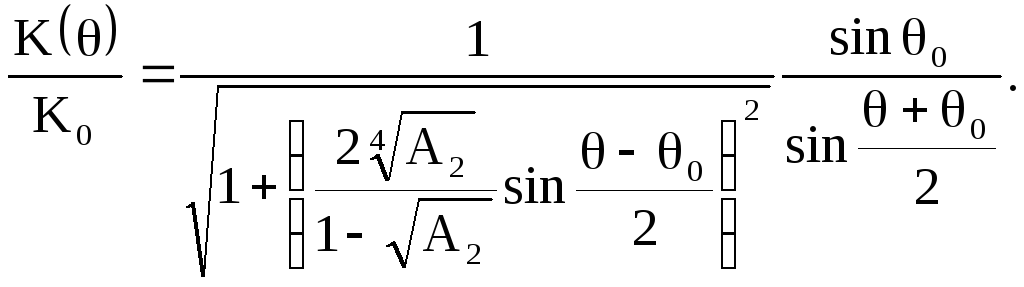
Учитывая, что
![]() получим АЧХ в относительном масштабе
как функцию нормированной частоты
получим АЧХ в относительном масштабе
как функцию нормированной частоты![]()
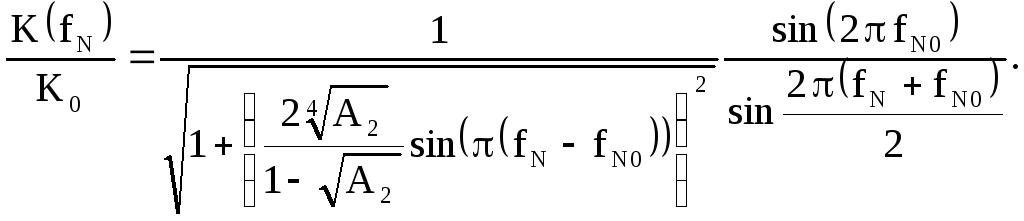 (2.40)
(2.40)
Важным параметром резонатора является полоса пропускания. Рисунок 2.55 иллюстрирует это понятие..

Рисунок 2.55. К определению полосы пропускания
Под нормированной полосой пропускания
ПNрезонатора
понимается разность нормированных
граничных частотfNg2-fNg1
вблизи резонансной частотыfN0,
определённая на заданном уровне![]() или при заданной допустимой неравномерности
в полосе пропускания
или при заданной допустимой неравномерности
в полосе пропускания![]() .
.
Под неравномерностью в полосе пропускания
понимается отношение максимального
коэффициента передачи в пределах полосы
пропускания к минимальному. В случае
резонатора максимальным является
резонансный коэффициент передачи, а
минимальным коэффициент передачи на
границе полосы пропускания при расстройке
относительно резонансной частоты fN0,
равной![]()
Таким образом, из (2.40) при
![]() получим
получим

При
![]()
![]() и
и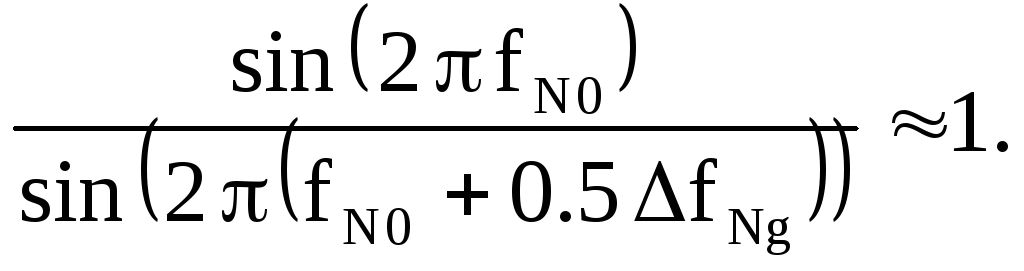
В этом случае последнее соотношение существенно упрощается
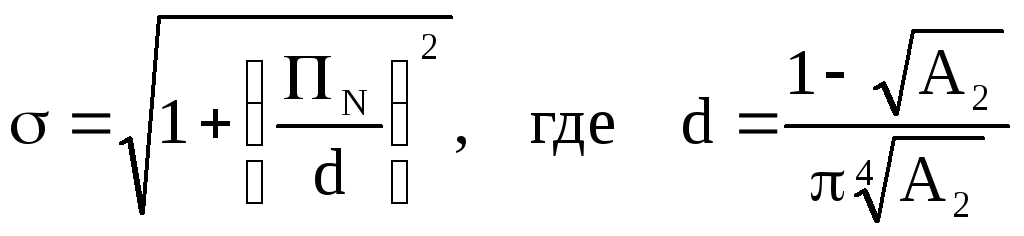 .
(2.41)
.
(2.41)
Следовательно,
![]() .
(2.42)
.
(2.42)
Пример. Требуется определить коэффициенты
A1,A2и М цифрового резонатора с нормированной
резонансной частотой![]() нормированной полосой пропускания
нормированной полосой пропускания![]() при неравномерности
при неравномерности![]() ,
резонансным коэффициентом передачи,
равным единице, и рассчитать АЧХ
резонатора.
,
резонансным коэффициентом передачи,
равным единице, и рассчитать АЧХ
резонатора.
1. Из (2.42) определим параметрd
![]()
2. Воспользовавшись соотношением для параметра d(2.41), выразим из негоA2черезd
![]()
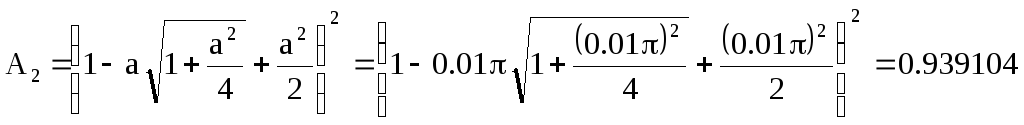 .
.
3. Из (2.34)выразимA1
![]() .
.
4. По (2.39) определим масштабный коэффициент
![]() 0.049266.
0.049266.
5. Найдём АЧХ по точной формуле для
системной функции (2.31), заменив zна![]() и найдя модуль полученного выражения
и найдя модуль полученного выражения
![]() .
.
Рассчитанная по этой формуле АЧХ приведена на рисунке 2.56.
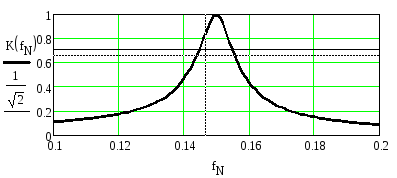
Рисунок 2.56. АЧХ резонатора при A1=-1.139214,A2=0.939104,M=0.049266
Из рисунка видно, что резонансный коэффициент передачи, резонансная частота и полоса пропускания резонатора соответствуют требованиям задания.
Определим импульсную характеристику резонатора. В разделе 2.5 показано, что импульсная характеристика линейной дискретной системы является обратным Z- преобразованием системной функции этой системы. Поэтому импульсная характеристика цифрового резонатора определяется соотношением
![]()
Обозначим подинтегральную функцию
![]() .
(2.43)
.
(2.43)
Представим дробь
![]() в виде суммы дробей
в виде суммы дробей
![]()
Способ такого представления детально описан в разделе 2.2.
В результате функция
![]() выражается следующим соотношением
выражается следующим соотношением
![]()
Импульсная характеристика определяется
суммой вычетов функции
![]()
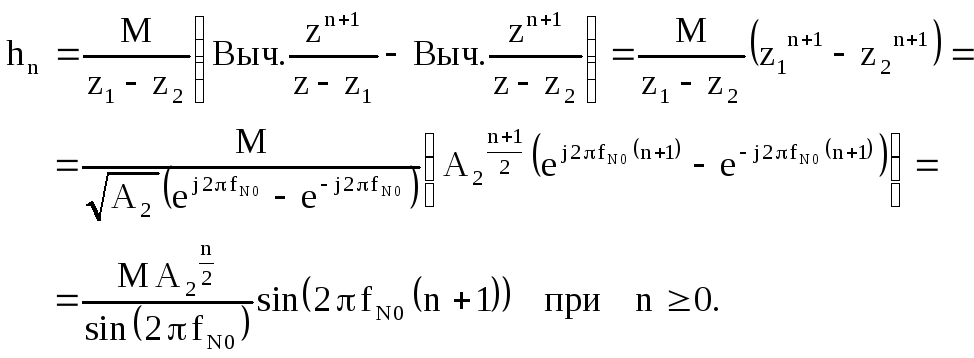 (2.44)
(2.44)
На рисунке 2.57 приведена импульсная характеристика резонатора, рассчитанная по полученной формуле при тех же значениях параметров, что и АЧХ рисунка 2.56.
Из рисунка и последнего соотношения
видно, что импульсная характеристика
резонатора при
![]() представляет собой затухающее
синусоидальное колебание. Чем ближеA2к единице, тем медленнее затухает
импульсная характеристика. Выше было
показано, что при приближенииA2к единице резонанс становится более
острым, полоса пропускания сужается.
Это соответствует общему положению о
том, что чем более инерционна система,
тем уже её полоса пропускания и наоборот.
представляет собой затухающее
синусоидальное колебание. Чем ближеA2к единице, тем медленнее затухает
импульсная характеристика. Выше было
показано, что при приближенииA2к единице резонанс становится более
острым, полоса пропускания сужается.
Это соответствует общему положению о
том, что чем более инерционна система,
тем уже её полоса пропускания и наоборот.
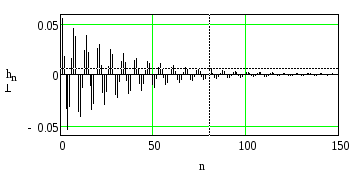
Рисунок 2.57. Импульсная характеристика резонатора
Из (2.33) следует, что модули первого и второго полюса резонатора одинаковы и равны
![]()
Линейная дискретная система устойчива, если модули всех её полюсов меньше единицы. Для резонатора это означает, что для обеспечения устойчивости коэффициент A2должен быть меньше единицы. ПриA2>1 резонатор не устойчив. В этом случае, как видно из (2.44), отсчеты импульсной характеристики неограниченно возрастают.
Таким образом, можно сделать следующие выводы:
импульсная характеристика резонатора бесконечна,
в устойчивом резонаторе импульсная характеристика является затухающей,
в неустойчивом резонаторе отсчёты импульсной характеристики неограниченно возрастают.
2.10.2. Расстроенная пара цифровых резонаторов
Рассмотрим цифровой фильтр, состоящий из двух последовательно включённых цифровых резонаторов, отличающихся друг от друга резонансными частотами (рисунок 2.58).
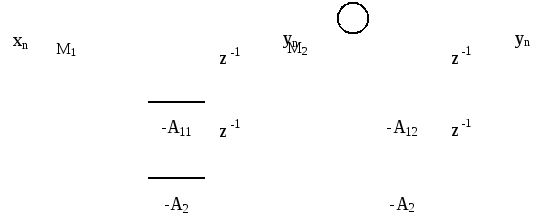
Рисунок 2.58. расстроенная пара цифровых резонаторов
АЧХ резонаторов приведены на рисунке
2.59. Если средняя нормированная частота
полосы пропускания фильтра должна быть
равна
![]() то частоты первого и второго резонаторов
резонаторов выбираются на основании
соотношений:
то частоты первого и второго резонаторов
резонаторов выбираются на основании
соотношений:
![]() (2.45)
(2.45)

Рисунок 2.59. АЧХ первого и второго резонаторов
Чтобы получить одинаковые резонансные коэффициенты передачи первого и второго резонаторов, масштабные коэффициенты должны быть равны:
![]()
![]() (2.46)
(2.46)
Коэффициенты системной функции
![]() и
и![]() определяются следующими соотношениями
определяются следующими соотношениями
![]() (2.47)
(2.47)
Учитывая (2.40), запишем выражения для коэффициентов передачи первого и второго резонаторов
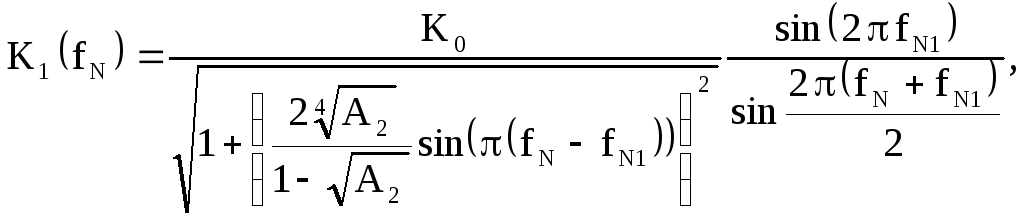
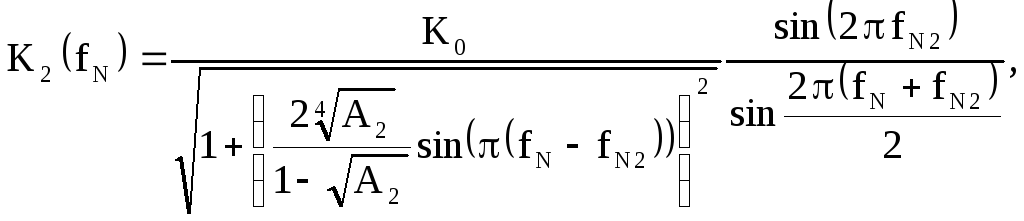
При малых расстройках относительно резонансных частот резонаторов последние соотношения упрощаются:
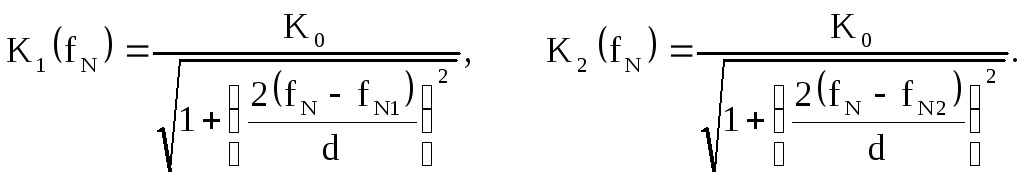
Найдём коэффициент передачи расстроенной пары с учётом (2.45)
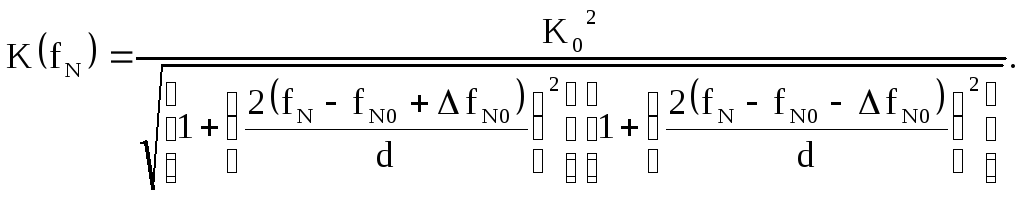
Введём обозначения:
![]() - нормированная абсолютная расстройка
текущей частоты относительно центральной
частоты полосы пропускания расстроенной
пары,
- нормированная абсолютная расстройка
текущей частоты относительно центральной
частоты полосы пропускания расстроенной
пары,
![]() обобщённая расстройка текущей частоты
относительно центральной частоты полосы
пропускания расстроенной пары,
обобщённая расстройка текущей частоты
относительно центральной частоты полосы
пропускания расстроенной пары,
![]() параметр расстройки резонансных частот
цифровых резонаторов.
параметр расстройки резонансных частот
цифровых резонаторов.
С учётом введённых обозначений перепишем последнее соотношение
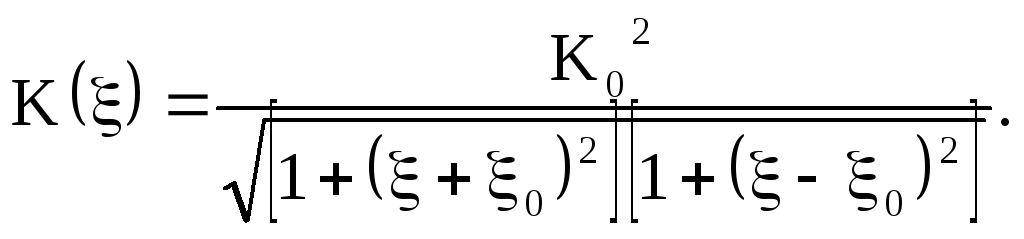 (2.48)
(2.48)
Коэффициент передачи расстроенной пары
на центральной частоте полосы пропускания
получим, подставляя в (2.48)
![]()
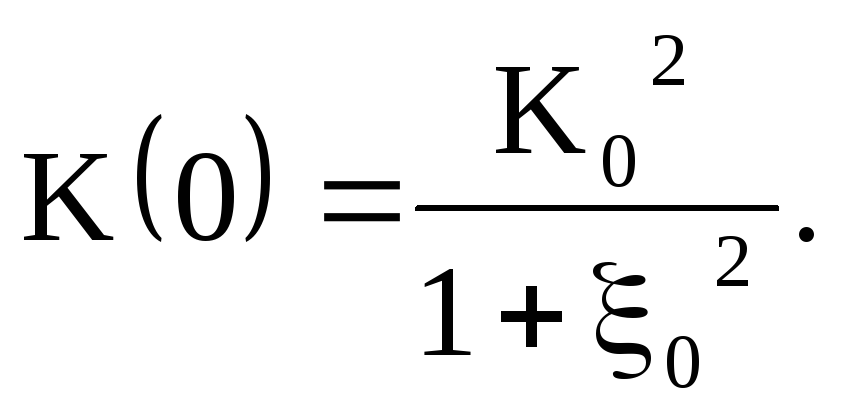 (2.49)
(2.49)
Из этого соотношения видно, что увеличение параметра расстройки приводит к уменьшению коэффициента передачи расстроенной пары на центральной частоте полосы пропускания.
На рисунке 2.60 приведены АЧХ расстроенной пары при разных значениях параметра расстройки. Из рисунка видно, что АЧХ может быть как одногорбой, так и двугорбой
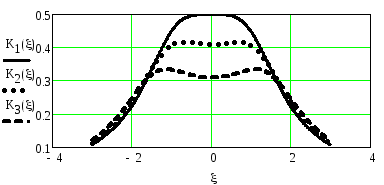
Рисунок 2.60. АЧХ расстроенной пары при 0 = 1 (K1()),0 = 1.2 (K2()),0 = 1.5 (K3())
Экстремумы функции
![]() совпадают с экстремумами функции под
знаком корня в выражении для
совпадают с экстремумами функции под
знаком корня в выражении для![]() .
Поэтому найдём производную этой функции
и приравняем её нулю
.
Поэтому найдём производную этой функции
и приравняем её нулю
![]()
Корни этого уравнения:
![]()
При
![]() существует только один действительный
корень уравнения
существует только один действительный
корень уравнения![]() ,
соответствующий максимуму одногорбой
АЧХ, при
,
соответствующий максимуму одногорбой
АЧХ, при![]() три действительных корня и двугорбая
АЧХ, при
три действительных корня и двугорбая
АЧХ, при![]() все три корня уравнения равны нулю, АЧХ
одногорбая на грани перехода в двугорбую.
При этом получается АЧХ с максимально
плоской вершиной. Взаимную расстройку
резонаторов при
все три корня уравнения равны нулю, АЧХ
одногорбая на грани перехода в двугорбую.
При этом получается АЧХ с максимально
плоской вершиной. Взаимную расстройку
резонаторов при![]() в аналоговой технике принято называть
критической.
в аналоговой технике принято называть
критической.
Определим полосу пропускания расстроенной
пары при
![]() .
Для этого найдем неравномерность АЧХ
в полосе пропускания, разделив
.
Для этого найдем неравномерность АЧХ
в полосе пропускания, разделив![]() на
на![]() ,
где
,
где![]() - обобщённая расстройка, соответствующая
границе полосы пропускания
- обобщённая расстройка, соответствующая
границе полосы пропускания
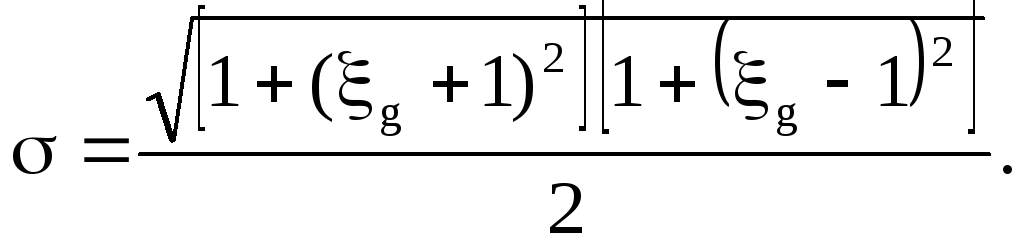
Из этого соотношения найдём
![]()
![]()
Таким образом, полоса пропускания расстроенной пары при критической расстройке определяется соотношением
![]() (2.50)
(2.50)
Пример. Требуется определить коэффициенты
A2,A11,A12,M1и М2расстроенной пары цифровых
резонаторов с центральной частотой
полосы пропускания![]() нормированной полосой пропускания
нормированной полосой пропускания![]() при неравномерности
при неравномерности![]() ,
максимальным коэффициентом передачи,
равным единице, и рассчитать АЧХ
расстроенной пары.
,
максимальным коэффициентом передачи,
равным единице, и рассчитать АЧХ
расстроенной пары.
1.По (2.50) определяем параметр d
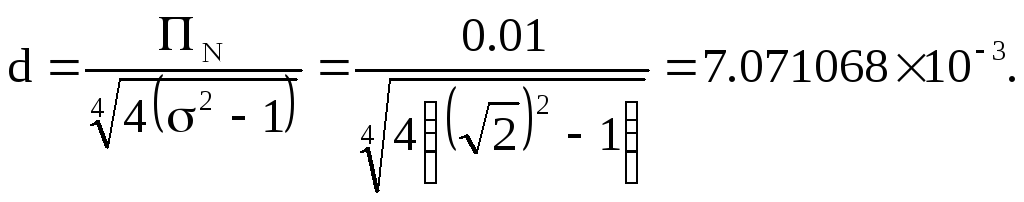
2. Находим коэффициент системной функцииA2
![]()
![]()
3. Определим величину нормированного отклонения резонансных частот резонаторов от нормированной средней частоты полосы пропускания расстроенной пары
![]() .
.
4. Определим резонансные частоты цифровых резонаторов (2.45)
![]()
![]()
5. Определим коэффициенты системной функции A11иA12(2.47)
![]()
6. По (2.49) найдём
резонансные коэффициенты передачи
резонаторов расстроенной пары при
требуемом значении коэффициента передачи
расстроенной пары на центральной частоте
полосы пропускания
![]()
![]()
7. По (2.46) определим масштабные коэффициенты на входах цифровых резонаторов расстроенной пары
![]()
![]() .
.
8. АЧХ расстроенной пары определяем по точной формуле как произведение модулей комплексных коэффициентов передачи первого и второго резонаторов
![]()
График АЧХ при
рассчитанных значениях коэффициентов
![]() приведён на рисунке 2.61.
приведён на рисунке 2.61.
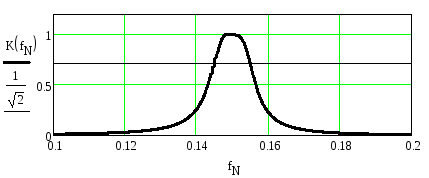
Рисунок 2.61. АЧХ расстроенной пары
Из рисунка видно, что максимальный коэффициент передачи, центральная частота полосы пропускания и полоса пропускания соответствуют требованиям задания.
Сравнение АЧХ расстроенной пары с АЧХ одного резонатора, имеющего такой же максимальный коэффициент передачи, такую же полосу пропускания и такую же центральную частоту полосы пропускания (рисунок 2.56), показывает, что у расстроенной пары крутизна скатов АЧХ больше, коэффициент передачи в полосе задерживания (при больших расстройках) меньше и вершина является более плоской, чем у АЧХ резонатора.
2.10.3. Режекторный фильтр на основе звена второго порядка
В разделе 2.8 рассмотрена системная функция и структурная схема типового звена второго порядка, а на рисунке 2.62 приведена схема звена второго порядка в частном случае равенства коэффициентов B0иB2единице.
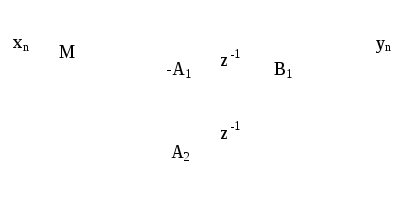
Рисунок 2.62. Режекторный фильтр
Системная функция фильтра определяется соотношением
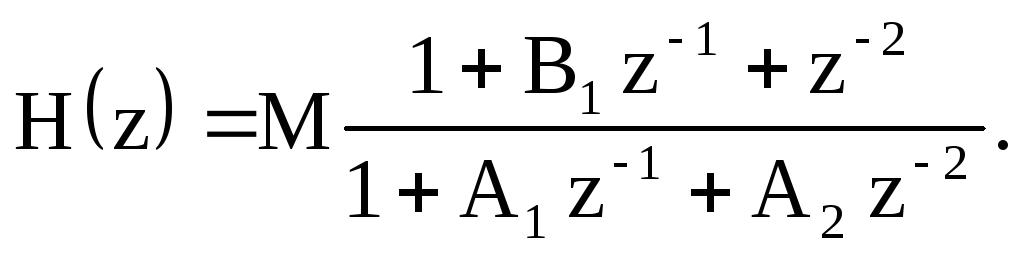 (2.51)
(2.51)
Комплексный коэффициент передачи фильтра равен
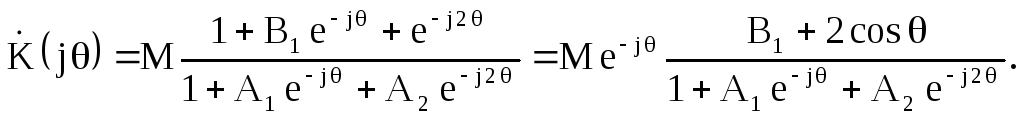
Определим значение нормированной частоты, на которой комплексный коэффициент передачи, а значит и его модуль равны нулю. Для этого приравняем нулю числитель дроби в выражении для комплексного коэффициента передачи
![]()
Из последнего соотношения найдём нормированную частоту режекции
![]()
Если нормированная частота режекции задана, то коэффициент системной функции
B1находится по формуле
![]() .
(2.52)
.
(2.52)
Потребуем равенства единице (может быть выбрано и другое значение) значений комплексных коэффициентов передачи на границах интервала Котельникова
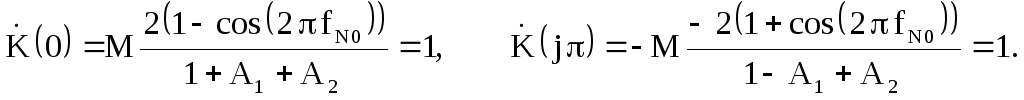
Из условия
![]() выразим
выразим![]() через
через![]() и
и![]()
![]() (2.53)
(2.53)
Подставив A1в
выражение для![]() найдём масштабный коэффициентM
найдём масштабный коэффициентM
![]() (2.54)
(2.54)
АЧХ режекторного фильтра рассчитывается по формуле
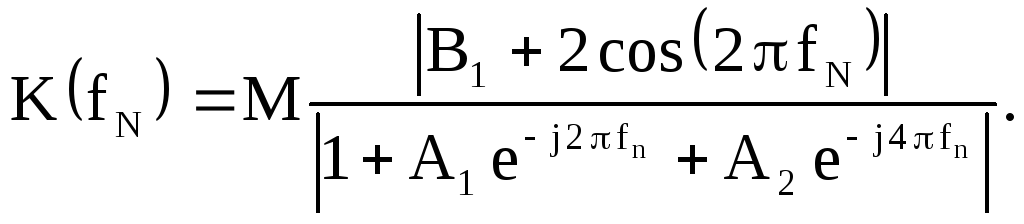 (2.55)
(2.55)
Входящие в последнее соотношение коэффициенты B1,A1иMпредварительно находятся по (2.52), (2.53) и (2.54) соответственно при заданном значении коэффициентаA2.
На рисунках 2.63 и 2.64 приведены АЧХ трёх режекторных фильтров при двух значениях коэффициента А2.
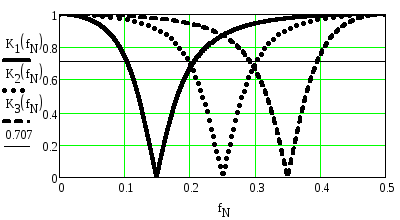
Рисунок 2.63. АЧХ трёх режекторных фильтров при A2=0.5
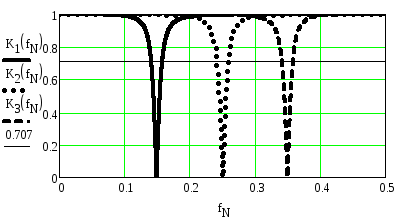
Рисунок 2.64. АЧХ трёх режекторных фильтров при A2=0.9
Из рисунков видно, что при перестройке фильтра по диапазону форма АЧХ практически не изменяется, особенно, при значениях A2, близких к единице. При приближенииA2 к единице область режекции сужается.
Определим полосу режекции при
неравномерности АЧХ в полосе режекции
![]() при частоте режекции
при частоте режекции![]()
В рассматриваемом случае случае
![]() и соотношение (2.55) преобразуется к виду
и соотношение (2.55) преобразуется к виду
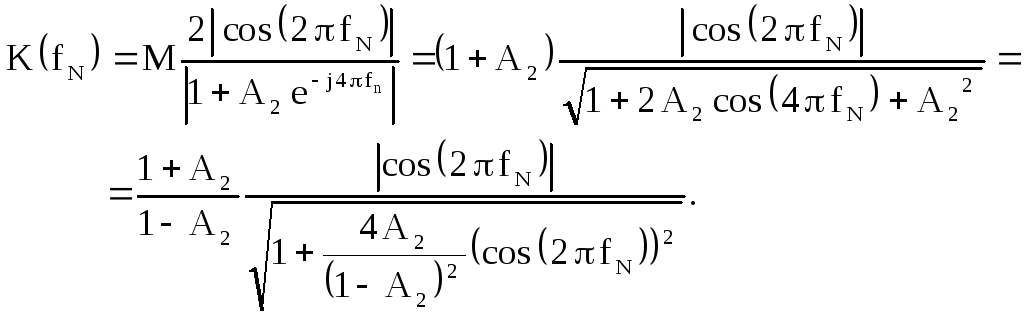
Обозначим
![]() и найдём зависимость коэффициента
передачи фильтра от отклонения
нормированной частоты от нормированной
частоты режекции
и найдём зависимость коэффициента
передачи фильтра от отклонения
нормированной частоты от нормированной
частоты режекции
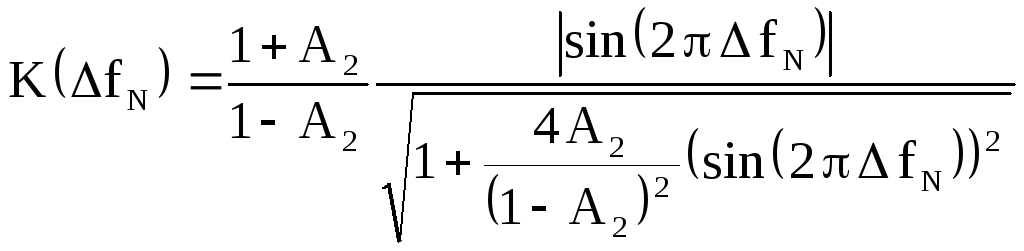 .
.
На границе полосы режекции
![]() коэффициент передачи фильтра равен
коэффициент передачи фильтра равен
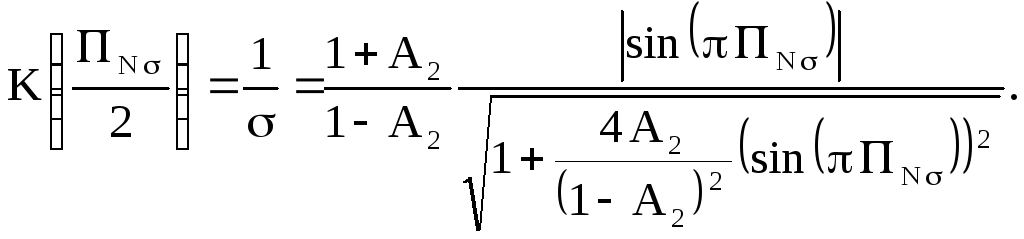
Из последнего соотношения получим
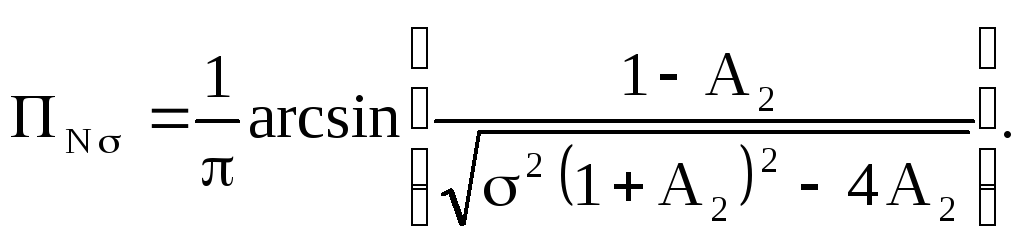 (2.56)
(2.56)
Это соотношение позволяет определить значение коэффициента A2, при котором обеспечивается требуемая полоса режекции
![]() (2.57)
(2.57)
где
 .
.
Пример. Требуется определить коэффициенты
A1,B1A2и М цифрового
режекторного фильтра с нормированной
частотой режекции![]() нормированной полосой режекции
нормированной полосой режекции![]() при неравномерности
при неравномерности![]() ,
максимальным коэффициентом передачи,
равным единице, и рассчитать АЧХ фильтра.
,
максимальным коэффициентом передачи,
равным единице, и рассчитать АЧХ фильтра.
1. Из (2.57) определим A2
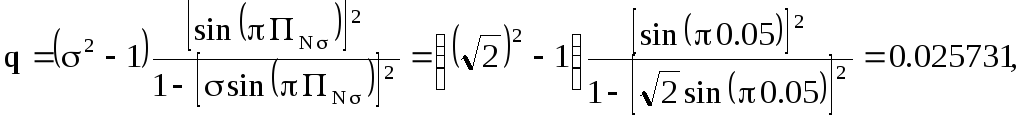
![]()
2. По (2.52) –(2.54) найдём коэффициенты B1.A1,M
![]() .
.
![]()
![]()
.
3. Построим график АЧХ по (2.55)
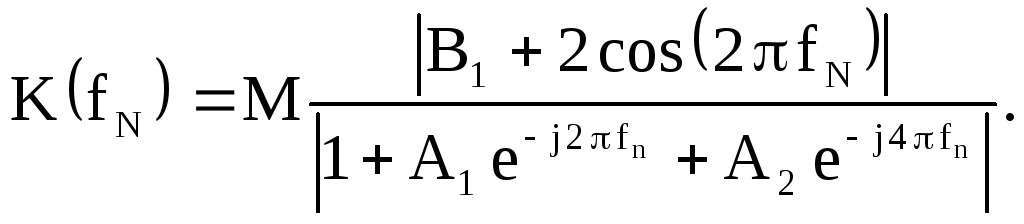
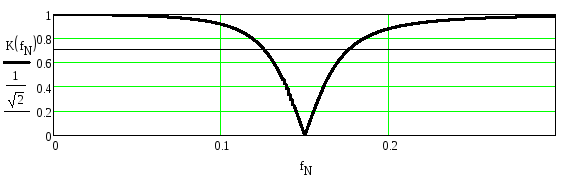
Рисунок 2.65. АЧХ режекторного фильтра
Из рисунка видно, что АЧХ фильтра удовлетворяет требованиям задания.
Определим импульсную характеристику режекторного фильтра. Для этого преобразуем выражение для системной функции (2.51)
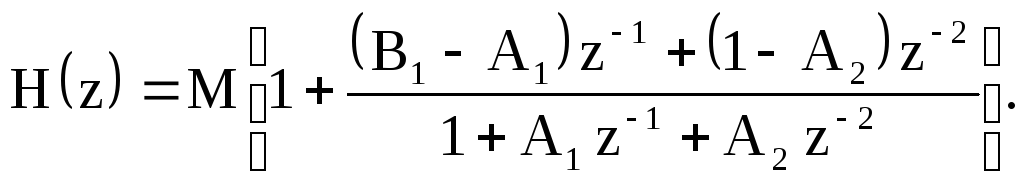
Введём обозначения:
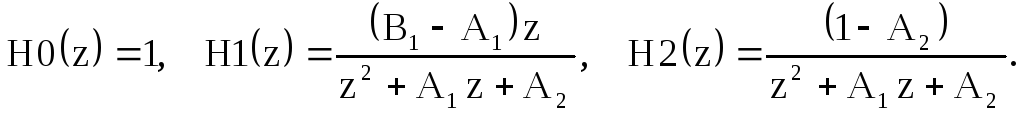
Тогда на основании свойства линейности Z-преобразования импульсную характеристику фильтра можно представить следующим образом:
![]() (2.58)
(2.58)
где
![]() обратныеZ-преобразования для
обратныеZ-преобразования для![]() соответственно.
соответственно.
В (2.1) было показано, что прямое
Z-преобразование единичного
отсчета равно единице, поэтому
последовательность![]() является единичным отсчетом
является единичным отсчетом

Для определения
![]() сначала преобразуем выражение для
сначала преобразуем выражение для![]()
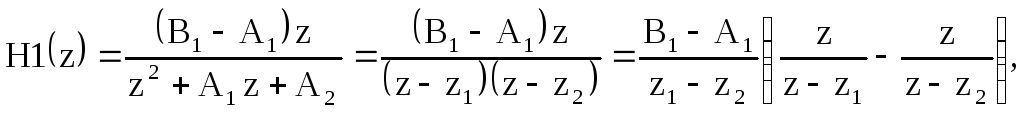
где
![]() и
и![]() -
корни квадратного уравнения
-
корни квадратного уравнения![]()
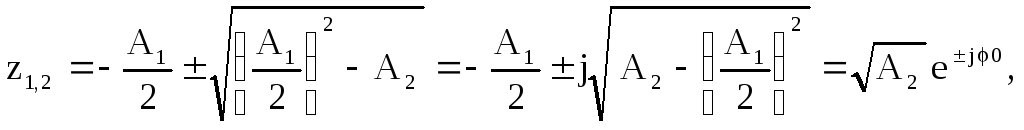
![]()
Из последнего соотношения видно, что
при
![]() нормированная
частота
нормированная
частота![]() на других частотах это равенство не
выполняется, но чем ближе отношение
на других частотах это равенство не
выполняется, но чем ближе отношение![]() к единице, тем меньше отличается частота
к единице, тем меньше отличается частота![]() от частоты режекции
от частоты режекции![]()
Последовательность h1n
является обратнымZ-преобразованием
функции![]()
![]()
Подинтегральная функция
![]() определяется следующим соотношением
определяется следующим соотношением
![]() .
.
Определим
![]()
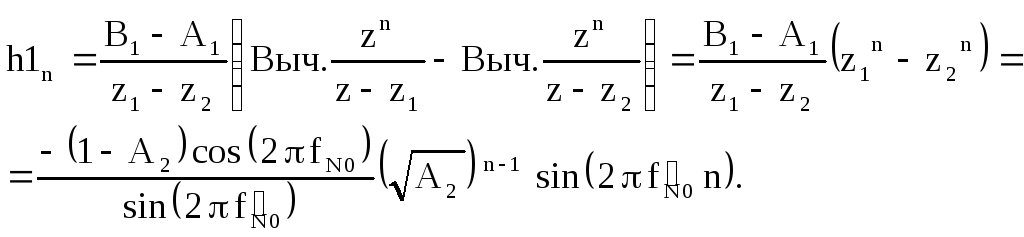
Последовательность h2n
является обратнымZ-преобразованием
функции![]()
![]()
Подинтегральная функция
![]() определяется следующим соотношением
определяется следующим соотношением
![]() .
.
Определим
![]()
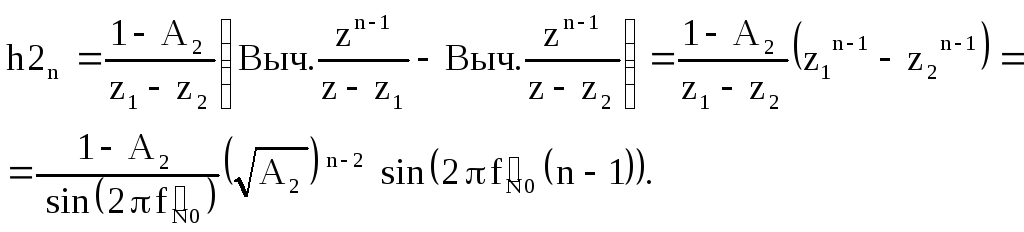
Подставив
![]() в (2.58) определим импульсную характеристику
режекторного фильтра
в (2.58) определим импульсную характеристику
режекторного фильтра
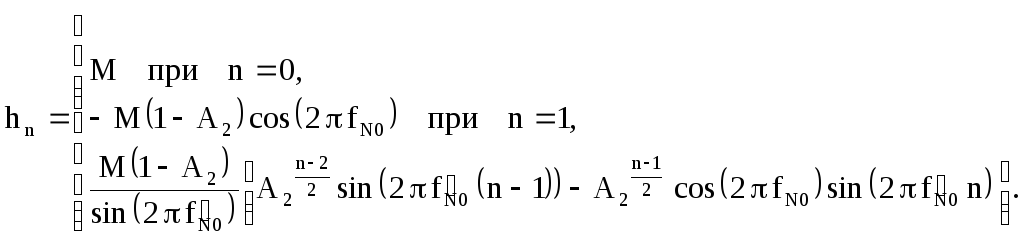
На рисунках 2.66-2.68 приведены импульсные характеристики при нормированной частоте режекции 0.15 и трёх значениях коэффициента A2. Из них видно, что импульсная характеристика режекторного фильтра представляет собой затухающее гармоническое колебание. При увеличении коэффициентаA2импульсная характеристика затухает медленнее, а амплитуда колебаний именьшается.

Рисунок 2.66. Импульсная характеристика при частоте режекции 0.15 и A2=0.50
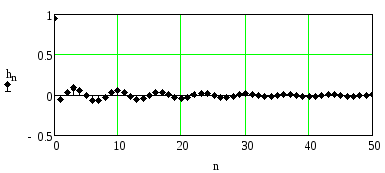
Рисунок 2.67. Импульсная характеристика при частоте режекции 0.15 и A2=0.90
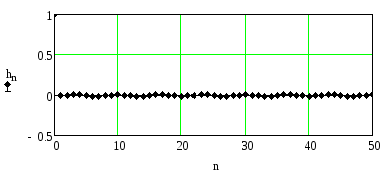
Рисунок 2.68. Импульсная характеристика при частоте режекции 0.15 и A2=0.99
2.11. Синтез нерекурсивных цифровых фильтров с линейной ФЧХ и прямоугольной
АЧХ методом ряда Фурье и «окна»
Задачей синтеза фильтра является
определение коэффициентов его системной
функции при заданных требованиях к АЧХ.
В случае фильтра с линейной ФЧХ и АЧХ,
определяемой рядом косинусов ((2.22),
(2.24)), этими коэффициентами являются
коэффициенты
![]() .
.
Из (2.22) и (2.24) видно, что функция
![]() ,
определяющая АЧХ фильтра, является
периодической функцией с периодом 2π.
,
определяющая АЧХ фильтра, является
периодической функцией с периодом 2π.
Пусть требуется выполнить синтез ФНЧ, у которого функция A(θ) стремится к функцииD(θ), показанной на рисунке 2.29 в интервале измененияθот –πдоπ, т.е. в пределах одного периода.

Рисунок 2.69 – Идеальная АЧХ ФНЧ
Разложение функции D(θ) в ряд Фурье позволяет определить коэффициенты
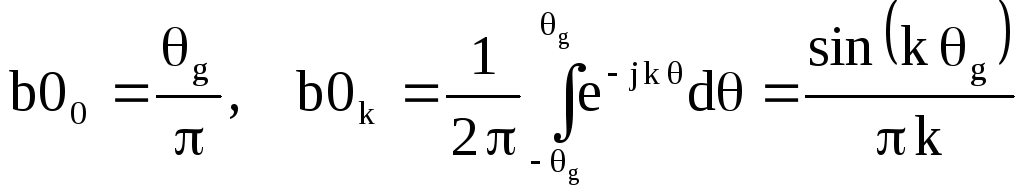 ,
(2.59)
,
(2.59)
где k= 1,2 ..k0,k0 =![]() .
.
В качестве примера приведем рассчитанные
по формулам (2.59) и (2.22) функцию
![]() и АЧХ К(θ) при θg
= π / 2,k0
=3.
и АЧХ К(θ) при θg
= π / 2,k0
=3.


Рисунок 2.70 – Функция
![]() и АЧХ К(θ) при θg
= π / 2,k0=3
и АЧХ К(θ) при θg
= π / 2,k0=3
Вместе с графиком реальной АЧХ K(θ) показана идеальная прямоугольная АЧХD(θ). Приk0=3 эти характеристики сильно отличаются друг от друга. Особенностью АЧХ являются пульсации как в полосе пропускания, так и в полосе задерживания.
На рисунках 2.71 и 2.72 приведены АЧХ фильтров при k0 =10 иk0=20 соответственно.
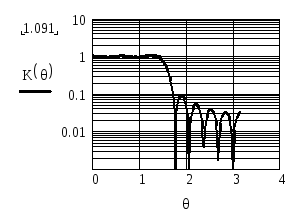
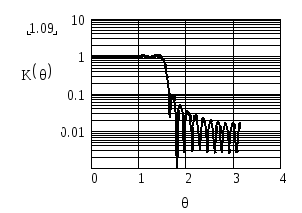
Рисунок 2.71 – АЧХ фильтра Рисунок 2.72 – АЧХ фильтра
при θg = π / 2, k0 = 10 при θg = π / 2, k0 = 20
На этих рисунках используется логарифмический масштаб по оси ординат для того, чтобы АЧХ была более наглядной в полосе задерживания.
Из рисунков видно, что увеличение длины импульсной характеристики (уменьшение количества отбрасываемых членов разложения Фурье), делая АЧХ более прямоугольной, не устраняет пульсации АЧХ. С увеличением m0частота пульсаций увеличивается, однако максимальный уровень первого бокового лепестка в полосе задерживания остается практически неизменным и равным 0.1.
Пульсации АЧХ вблизи точек разрыва функции, связанные с ограничением членов разложения в ряд Фурье, получили название явления Гиббса.
Для уменьшения пульсаций рядом специалистов по цифровой обработке сигналов было предложено использование так называемых «оконных функций».
Сущность метода состоит в следующем: вместо коэффициентов системной функции bkиспользуют коэффициенты
![]() (2.60)
(2.60)
где Wk -k-ый отсчет оконной функции.
Простому ограничению ряда Фурье соответствует прямоугольное окно
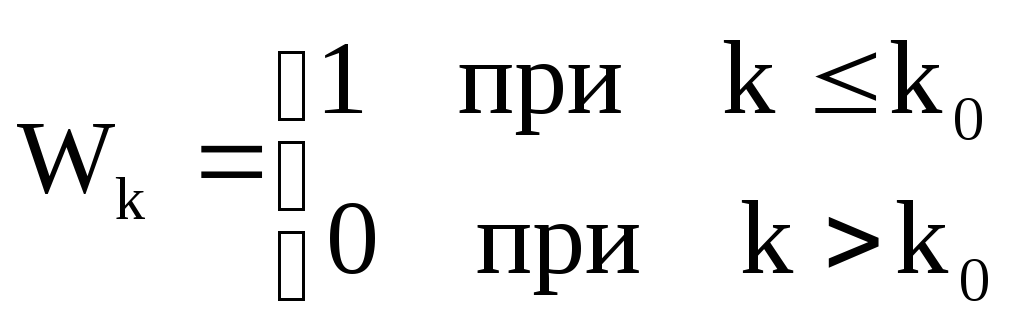
Несколько других функций приведено в таблице 2.1.
На рисунках 2.73 и 2.74 показаны АЧХ рисунков 2.71 и 2.72 соответственно после операции сглаживания с использованием окна Хемминга. Из сопоставления АЧХ до сглаживания и после него видно, что эта операция приводит к существенному (примерно на 40 дБ) ослаблению пульсаций, но и к расширению переходной полосы между полосой пропускания и полосой задерживания фильтра.
Таблица 2.1. Функции окна
|
Название окна |
Функция окна |
|
Окно фон Ганна (приподнятый косинус) |
|
|
Окно Хемминга |
|
|
Окно Блэкмана |
|
|
Окно Ланцоша |
|
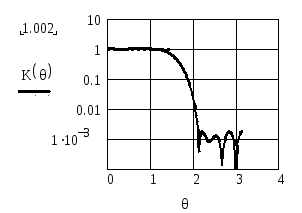
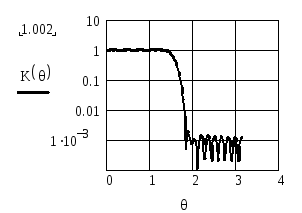
Рисунок 2.73. АЧХ при θg = π / 2, Рисунок 2.74. АЧХ фильтра при θg = π / 2,k0=10 и сглаживанием пульсацийk0=20 и сглаживанием пульсаций
функцией Хемминга функцией Хемминга
Описанный метод синтеза рассмотрен на примере фильтра нижних частот. Однако его нетрудно распространить на фильтры других типов.
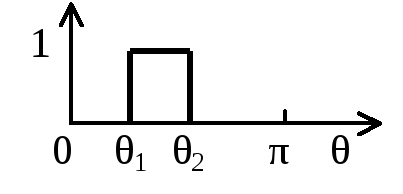
Например, АЧХ полосового фильтра с граничными значениями полосы θ1иθ2можно представить в виде разности АЧХ ФНЧ, как это показано на рисунке 2.75.

Рисунок 2.75 – Представление АЧХ полосового фильтра в виде разности АЧХ ФНЧ
D(θ)=D2(θ) –D1(θ)
Такое представление АЧХ позволяет определить коэффициенты разложения в ряд Фурье bmкак разность соответствующих коэффициентов разложений в ряд Фурье АЧХ ФНЧ
![]() (2.61)
(2.61)
Аналогичным образом находятся коэффициенты разложения для режекторного фильтра (РФ) и фильтра верхних частот (ФВЧ)
В таблице 2.2 приведены значения коэффициентов разложения АЧХ для всех типов фильтров. Оконные функции используютcя при синтезе всех типов фильтров одинаково.
Таблица 2.2. Коэффициенты
разложения в ряд Фурье функции
![]() ,
,
определяющей АЧХ фильтра
|
Тип фильтра |
Коэффициенты b0n |
|
ФНЧ
|
|
|
ФВЧ
|
|
|
ПФ
|
|
|
РФ
|
|
Пример.
Выполнить синтез полосового фильтра с
линейной ФЧХ методом ряда Фурье и «окна»
Блэкмана. Длина импульсной характеристики
фильтра N=101,
средняя нормированная частота полосы
пропускания fN0
=0.25, нормированная полоса пропускания
![]() .
Построить график АЧХ фильтра.
.
Построить график АЧХ фильтра.
1. По (2.61) и (2.60) рассчитываем коэффициенты системной функции
Ниже приводится фрагмент расчёта в программной среде Mathcad
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
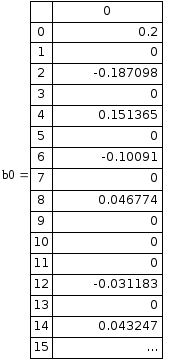
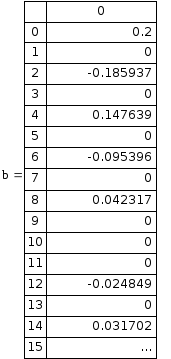
2. По (2.22) рассчитываем АЧХ при отсутствии и при наличии «окна»
![]()
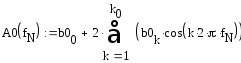
![]()

![]()
На рисунке 2.76 представлены две АЧХ, рассчитанные при наличии K(fN) и при отсутствииK0(fN) «окна» с использованием логарифмического масштаба по оси ординат. Логарифмический масштаб позволяет детально рассмотреть АЧХ в полосе задерживания, но при этом не видны детали АЧХ в полосе пропускания. Для их наблюдения на рисунке 2.77 приведён фрагмент АЧХ рисунка 2.76 в линейном масштабе.
Из рисунков видно, что применение оконной функции позволяет более чем на два порядка уменьшить максимальный уровень пульсаций в полосе задерживания, но при этом уменьшается крутизна спада АЧХ
Расчётная нормированная полоса
пропускания
![]() обеспечивается на уровне 0.5 и при наличии,
и при отсутствии окна, т.е. наблюдается
значительная неравномерность АЧХ в
пределах полосы пропускания.
обеспечивается на уровне 0.5 и при наличии,
и при отсутствии окна, т.е. наблюдается
значительная неравномерность АЧХ в
пределах полосы пропускания.

Рисунок 2.76. АЧХ, рассчитанные методом разложения в ряд Фурье при наличии и отсутствии окна Блэкмана и при N=101 (логарифмический масштаб)
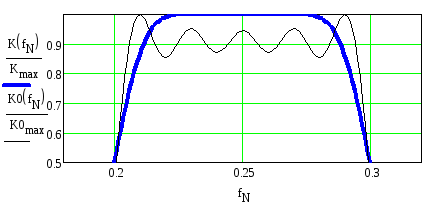
Рисунок 2.77. Фрагмент АЧХ рисунка 2.76 в линейном масштабе
На рисунках 2.78 и 2.79 приведены импульсные характеристики фильтра при наличии и отсутствии оконной функции.
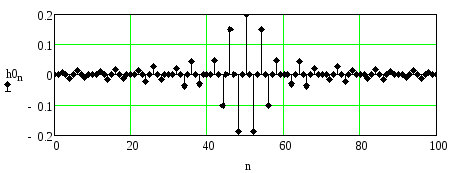
Рисунок 2.78. Импульсная характеристика фильтра без оконной функции
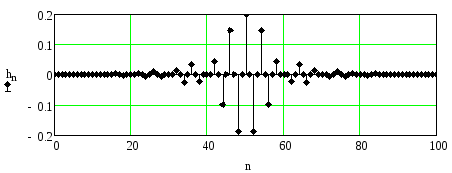
Рисунок 2.79. Импульсная характеристика фильтра с использованием окна Блэкмана
Из рисунков видно, что вблизи центрального отсчёта импульсные характеристики практически не отличаются друг от друга, однако по мере удаления от центрального отсчёта отличие характеристик становится более заметным из-за уменьшения абсолютных значений отсчётов из-за влияния оконной функции.
2.12. Синтез нерекурсивных цифровых фильтров с линейной ФЧХ и АЧХ,
описываемой функцией без разрывов, методом ряда Фурье
Из рисунков 2.71 и 2.72 видно, что максимум пульсаций Гиббса имеет место вблизи точки разрыва функции, задающей требуемую АЧХ фильтра. Поэтому для уменьшения пульсаций целесообразно использовать функции без разрывов.
Одной из таких функций является широко используемая функция Гаусса. АЧХ ФНЧ, задаваемая этой функцией, представляется следующим соотношением
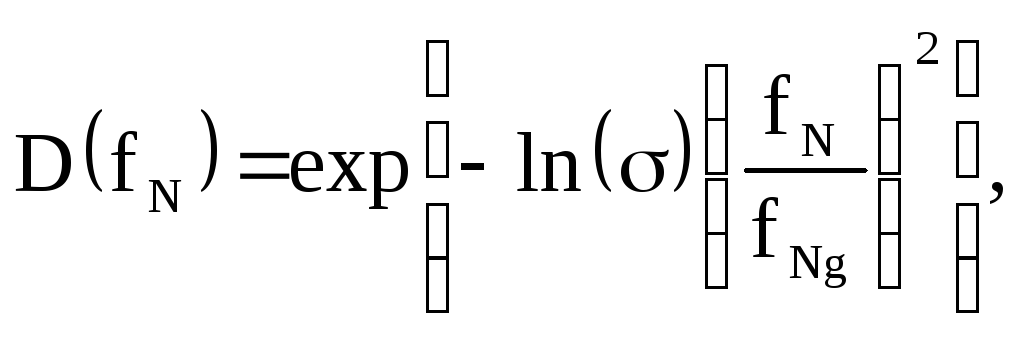 (2.62)
(2.62)
где
![]() -
неравномерность АЧХ в полосе пропускания
фильтра – отношение максимального
коэффициента передачи к минимальному
коэффициенту передачи в пределах полосы
пропускания,
-
неравномерность АЧХ в полосе пропускания
фильтра – отношение максимального
коэффициента передачи к минимальному
коэффициенту передачи в пределах полосы
пропускания,![]() - граничная частота полосы пропускания
фильтра.
- граничная частота полосы пропускания
фильтра.
Отсчёты импульсной характеристики фильтра определяются соотношениями для коэффициентов Фурье
![]() (2.63)
(2.63)
где
![]() -
длина импульсной характеристики
(нечётное число).
-
длина импульсной характеристики
(нечётное число).
Приведенные интегралы легко определяются в программной среде Mathсad.
Фактическая АЧХ находится по формуле
![]() (2.64)
(2.64)
На рисунке 2.80 приведены требуемая и
реальная АЧХ гауссовского ФНЧ при
![]()
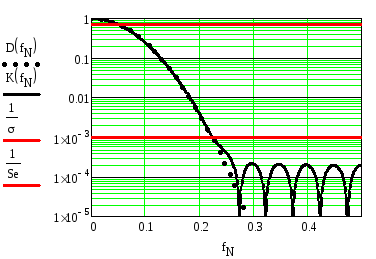
Рисунок 2.80. Требуемая и реальная АЧХ гауссовского ФНЧ
при
![]()
Под ослаблением в полосе задерживания или селективностью фильтра Seпонимается отношение максимального коэффициента передачи в полосе пропускания к максимальному коэффициенту передачи в полосе задерживания
Из рисунка видно, что максимальный
коэффициент передачи в полосе задерживания
(максимальный уровень пульсаций в полосе
задерживания) равен
![]() ,
а максимальный коэффициент передачи в
полосе пропускания равен единице,
поэтомуSe= 1000. Для
обеспечения такой селективности
потребовалась импульсная характеристика
длинойN=19.
,
а максимальный коэффициент передачи в
полосе пропускания равен единице,
поэтомуSe= 1000. Для
обеспечения такой селективности
потребовалась импульсная характеристика
длинойN=19.
В разделе 2.9.1 показано, что импульсная характеристика фильтра с линейной ФЧХ симметрична относительно центрального отсчёта b0, по обе стороны относительно центрального отсчёта располагаются отсчётыb1,b2, . ., нумерация которых ведётся от центра.
Для перехода к импульсной характеристике
с последовательной нумерацией отсчётов
от 0 до
![]() нужно воспользоваться следующим
соотношением:
нужно воспользоваться следующим
соотношением:
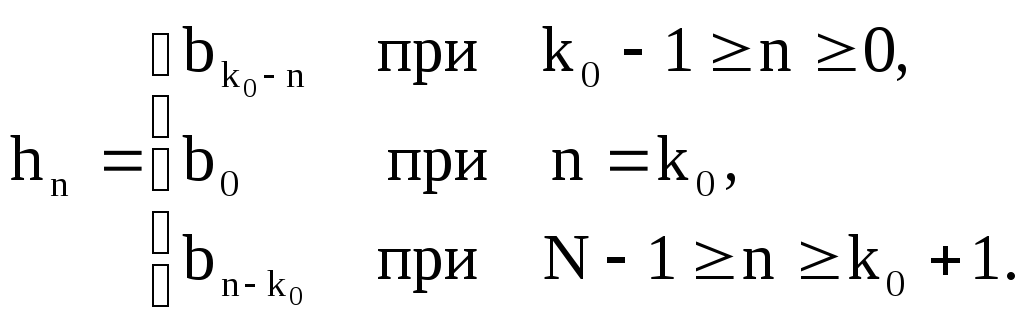
Импульсная характеристика гауссовского
ФНЧ при
![]() приведена на рисунке 2.81
приведена на рисунке 2.81
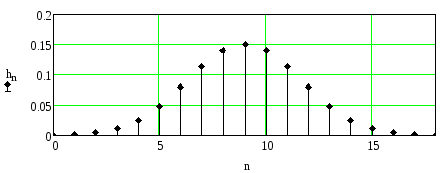
Рисунок 2.81. Импульсная характеристика гауссовского ФНЧ
при
![]()
При проектировании фильтра наряду с
параметрами
![]() задаётся селективностьSe.
При требуемой АЧХ длина импульсной
характеристикиNвыбирается
так, чтобы обеспечить заданную
селективность.
задаётся селективностьSe.
При требуемой АЧХ длина импульсной
характеристикиNвыбирается
так, чтобы обеспечить заданную
селективность.
В ПРИЛОЖЕНИИ А приведена программа синтеза гауссовского ФНЧ в программной среде Mathcad. Программа требует задания ориентировочного значения длины импульсной характеристики, которое затем уточняется.
В таблице 2.3 приведены значения длины
импульсной характеристики ФНЧ при
заданных значениях
![]() которые можно использовать при работе
с программой.
которые можно использовать при работе
с программой.
Из таблицы видно, что уменьшение граничной частоты и увеличение требуемой селективности требует увеличения длины импульсной характеристики фильтра.
Таблица 2.3. Зависимость длины импульсной характеристики ФНЧ
от требуемой селективности
и граничной частоты при
![]()
|
Нормированная граничная частота fNg |
Длина импульсной характеристики N | |
|
Se=100 |
Se=1000 | |
|
0.025 |
29 |
33 |
|
0.050 |
15 |
19 |
|
0.075 |
11 |
13 |
|
0.100 |
9 |
9 |
АЧХ полосового фильтра, задаваемая функцией Гаусса, определяется следующим соотношением
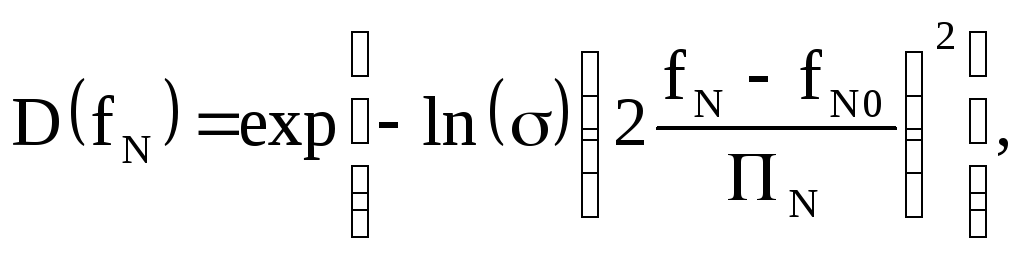 (2.65)
(2.65)
где
![]() - средняя нормированная частота полосы
пропускания,
- средняя нормированная частота полосы
пропускания,![]() -
нормированная полоса пропускания,
-
нормированная полоса пропускания,![]() - неравномерность АЧХ в полосе пропускания.
- неравномерность АЧХ в полосе пропускания.
Расчёт импульсной характеристики и АЧХ выполняется по (2.63) и (2.64).
На рисунке 2.82 приведены требуемая и
реальная АЧХ гауссовского полосового
фильтра при
![]() ,
а на рисунке 2.83 его импульсная
характеристика
,
а на рисунке 2.83 его импульсная
характеристика
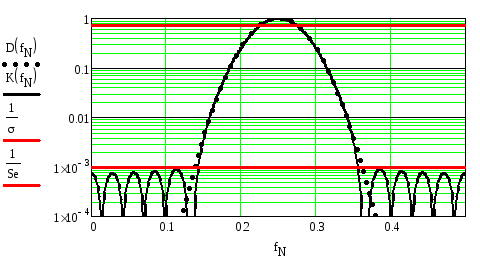
Рисунок 2.82. АЧХ гауссовского полосового фильтра при
![]()
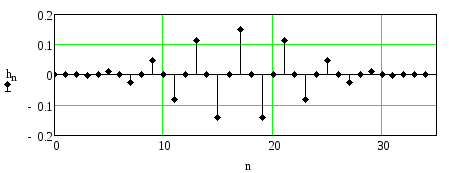
Рисунок 2.83. Импульсная характеристика гауссовского полосового фильтра
при
![]()
В таблице 2.4 приведены значения длины линии задержки при разных значениях полосы пропускания и селективности, на которые можно ориентироваться при синтезе фильтра по программе, приведённой в ПРИЛОЖЕНИИ Б.
Сравнение таблиц 2.3 и 2.4 показывает, что при одинаковых требованиях к селективности и одинаковых значениях полосы пропускания длина импульсной характеристики полосового фильтра примерно в два раза больше длины импульсной характеристики ФНЧ.
Таблица 2.4. Зависимость длины импульсной характеристики ПФ от
требуемой селективности и
граничной частоты при fN0
= 0.25 и![]()
|
Нормированная полоса ПN |
Длина импульсной характеристики N | |
|
Se=100 |
Se=1000 | |
|
0.025 |
55 |
69 |
|
0.050 |
29 |
35 |
|
0.075 |
21 |
25 |
|
0.100 |
17 |
17 |
Важным параметром любого фильтра
является коэффициент прямоугольности,
под которым понимают отношение полосы
пропускания фильтра при заданной
селективности
![]() к
полосе пропускания при заданной
неравномерности
к
полосе пропускания при заданной
неравномерности![]()
![]() .
.
Входящая в (2.65) разность
![]() представляет собой расстройку текущей
частоты относительно средней частоты
полосы пропускания фильтра. При
коэффициенте передачи
представляет собой расстройку текущей
частоты относительно средней частоты
полосы пропускания фильтра. При
коэффициенте передачи![]() удвоенная расстройка является полосой
пропускания при заданной селективности
удвоенная расстройка является полосой
пропускания при заданной селективности![]()
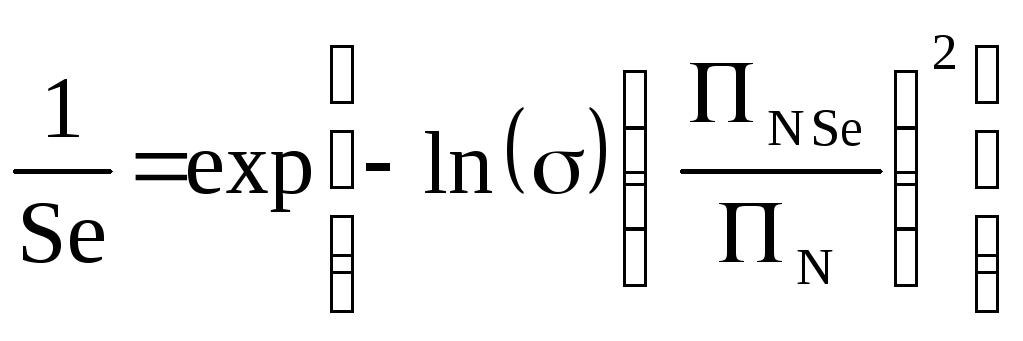 .
.
Из последнего соотношения получим
![]()
Из (2.62) видно, что это соотношение справедливо и для ФНЧ.
Таким образом, коэффициент прямоугольности гауссовского фильтра определяется значениями требуемой селективности и неравномерности коэффициента передачи в полосе пропускания. С увеличением селективности коэффициент прямоугольности, к сожалению, тоже увеличивается.
Этот недостаток устраняет модификация показателя экспоненты функции Гаусса. Так, для описания требуемой АЧХ ФНЧ вместо (2.65) можно использовать функцию
![]() (2.66)
(2.66)
Константы
![]() зависят от нормированной граничной
частоты
зависят от нормированной граничной
частоты![]() неравномерности АЧХ в полосе пропускания
неравномерности АЧХ в полосе пропускания![]() ,
требуемой селективностиSeи коэффициента прямоугольности
,
требуемой селективностиSeи коэффициента прямоугольности![]()
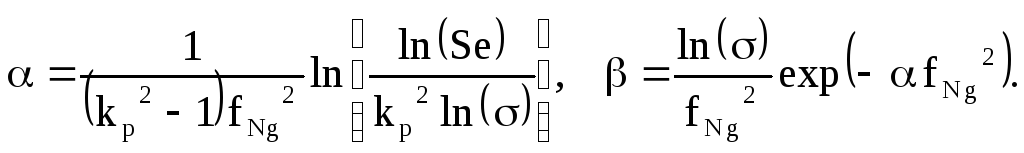 (2.67)
(2.67)
На рисунке 2.84 приведены требуемая и
реальная АЧХ ФНЧ, синтезированного с
использованием модифицированной функции
Гаусса при
![]()
![]()
![]() ,
а на рисунке 2.85– его импульсная
характеристика.
,
а на рисунке 2.85– его импульсная
характеристика.
Сравнение этих характеристик с
соответствующими характеристиками
гауссовского ФНЧ показывает, что
уменьшение коэффициента прямоугольности
от значения
![]() в гауссовском ФНЧ до значения
в гауссовском ФНЧ до значения![]() в ФНЧ с модифицированной АЧХ приводит
к увеличению длины импульсной
характеристики от 33 до 129 и соответствующему
увеличению длины линии задержки фильтра.
в ФНЧ с модифицированной АЧХ приводит
к увеличению длины импульсной
характеристики от 33 до 129 и соответствующему
увеличению длины линии задержки фильтра.
Программа синтеза ФНЧ с модифицированной АЧХ Гаусса отличается от программы, приведённой в ПРИЛОЖЕНИИ А только видом функции D(fN) ((2.67) и (2.66)) и введением в исходные данные значения коэффициента прямоугольности.
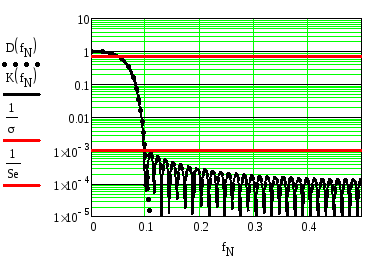
Рисунок 2.84. Требуемая D(fN) реальнаяK(fN) АЧХ ФНЧ при
![]()
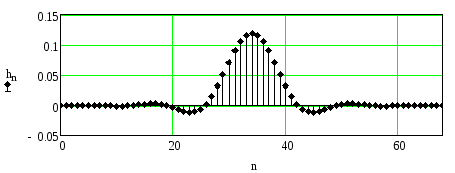
Рисунок 2.85. Импульсная характеристика ФНЧ при
![]()
При синтезе полосового фильтра с заданным значением коэффициента прямоугольности вместо (2.65) используется функция
![]() (2.68)
(2.68)
Коэффициенты
![]() определяются следующими соотношениями
определяются следующими соотношениями
 (2.69)
(2.69)
На рисунке 2.86 приведены требуемая и
реальная АЧХ полосового фильтра,
синтезированного с использованием
модифицированной функции Гаусса при
![]()
![]()
![]()
![]() ,
а на рисунке 2.87 – его импульсная
характеристика.
,
а на рисунке 2.87 – его импульсная
характеристика.
Сравнение рисунков 2.86 и 2.87 с рисунками 2.82 и 2.83 соответственно показывает, что, как и в случае ФНЧ, уменьшение коэффициента прямоугольности требует увеличение длины линии задержки.
Программа синтеза полосового фильтра с модифицированной гауссовской АЧХ отличается от программы ПРИЛОЖЕНИЯ Б только тем, что функция (2.65) заменяется соотношениями (2.69) и (2.68), а в исходные данные вводится ещё значение коэффициента прямоугольности kp.
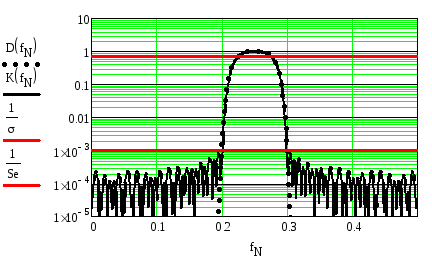
Рисунок 2.86. Требуемая и
реальная АЧХ полосового фильтра при![]()
![]()
![]()
![]()
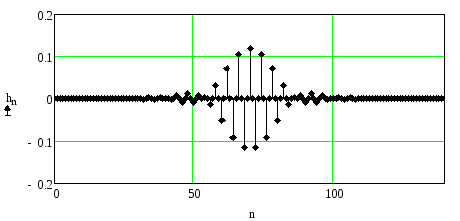
Рисунок 2.87. Импульсная характеристика полосового фильтра при
![]()
![]()
![]()
2.13. Синтез КИХ - фильтров с линейной ФЧХ методом наименьших квадратов
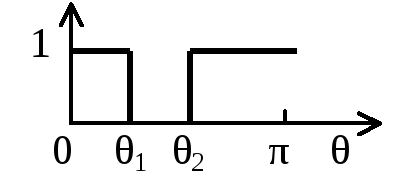
На рисунке приведена функция D(θ) - идеальная АЧХ полосового фильтра в полосе пропускания и полосе задерживания и функцияA(θ), определяющая реальную АЧХ.K()
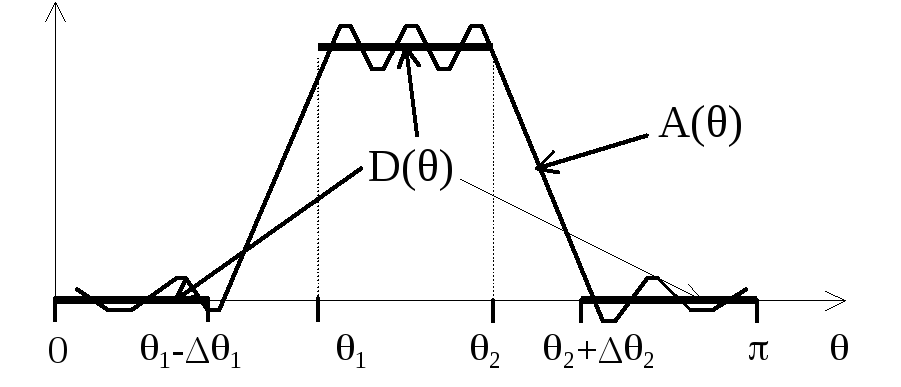
Рисунок 2.88 - Функция A(θ) и функцияD(θ), описывающая идеальную АЧХ

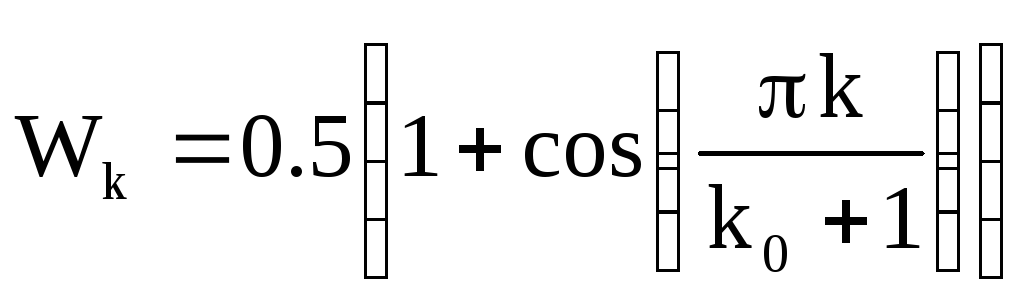
 ,
где L=1 илиL=2
,
где L=1 илиL=2