2.Цифровые фильтры

Введение

Фильтрация является одним из видов обработки как аналоговых, так и цифровых сигналов, нашедших широчайшее применение во всех областях деятельности человека.

В телекоммуникационных приложениях фильтрация используется для ограничения спектра сигнала, для селекции сигналов, для режекции помех.

Цифровой фильтр выполняет те же функции, что и аналоговый, но отличается своей реализацией. В данной теме рассматриваются алгоритмы реализации цифровых фильтров, их анализ и синтез.

Математическим аппаратом цифровой фильтрации является Z– преобразование.

Поэтому сначала рассматриваются основные свойства Z- преобразования, основные характеристики цифровых фильтров, а затем вопросы их синтеза.

В данную тему входят следующие разделы:

2.1. Прямое Z-преобразование и его свойства

2.2. Обратное Z-преобразование

2.3. Дискретные линейные системы, их свойства и характеристики

2.4. Определение выходного сигнала линейной инвариантной относительно сдвига

дискретной системы по входному сигналу и импульсной характеристике

2.5. Разностное уравнение и системная функция дискретной линейной системы. Связь

между системной функцией и импульсной характеристикой

2.6. Связь между комплексным коэффициентом передачи и системной функцией

дискретной линейной системы

2.7. Устойчивость линейной дискретной системы

2.8. Классификация и формы программной реализации цифровых фильтров

2.9. Фильтры с конечной импульсной характеристикой

2.9.1. Фильтр с линейной ФЧХ

2.9.2. Однородный фильтр

2.9.3. Триангулярный фильтр

2.9.4. Гребенчатый фильтр

2.10. Рекурсивные цифровые фильтры

2.10.1. Цифровой резонатор

2.10.2. Расстроенная пара цифровых резонаторов

2.10.3. Режекторный фильтр на основе звена второго порядка

2.11. Синтез нерекурсивных цифровых фильтров с линейной ФЧХ и прямоугольной

АЧХ методом ряда Фурье и «окна»

2.12. Синтез нерекурсивных цифровых фильтров с линейной ФЧХ и АЧХ,

описываемой функцией без разрывов, методом ряда Фурье

2.13. Синтез КИХ - фильтров с линейной ФЧХ методом наименьших квадратов

2.14. Синтез нерекурсивных цифровых фильтров с линейной ФЧХ методом

наилучшей равномерной (чебышевской) аппроксимации

2.15. Синтез БИХ - фильтров по принципу инвариантности импульсной

характеристики

2.16. Синтез БИХ – фильтров методом билинейного Z– преобразования

2.1. Прямое Z- преобразование и его свойства

Прямым Z-преобразованиемдискретной последовательностиx_n, гдеn= 0,1,2.., называется функция комплексного переменногоz, определяемая следующим соотношением

. (2.1)

Функция определена для тех значенийz, при которых ряд сходится.

Здесь и в дальнейшем последовательность отсчётов обозначается строчной, а ее Z-преобразование той же прописной буквой.

Рассмотрим примеры определения прямого Z-преобразования.

Пример 1. Единичный отсчёт

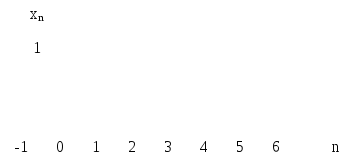
Рисунок 2.1. Единичный отсчёт

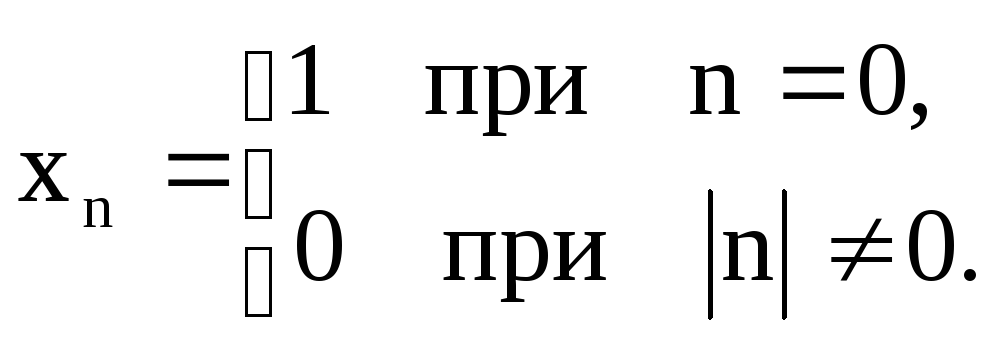
Из последнего соотношения следует, что прямое Z-преобразование единичного отсчета равно единице при всех значенияхz, отличных от нуля.

Пример 2. Единичный скачок

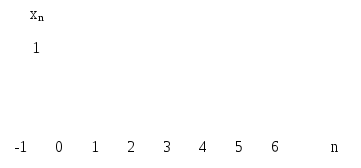
Рисунок 2.2. Единичный скачок

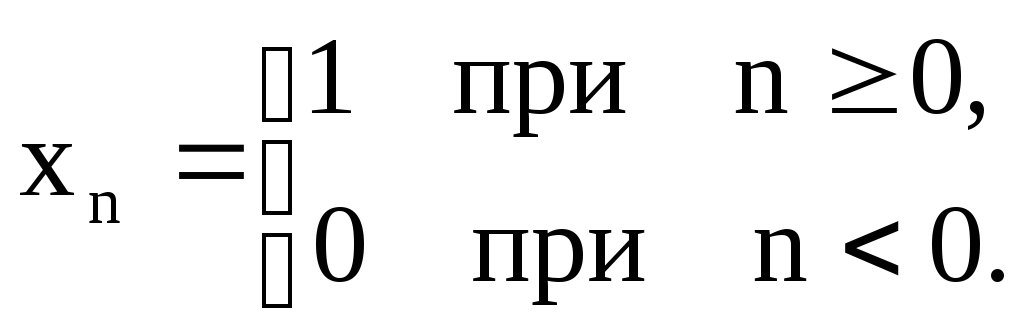
В последнем соотношении припредставляет собой сумму членов бесконечно убывающей геометрической прогрессии. Известно, что сумма членов бесконечно убывающей геометрической прогрессии равна первому члену, делённому на (1-знаменатель прогрессии). У данной прогрессии первый член (приn=0) равен единице, а знаменатель прогрессии

На рисунке 2.3 показана плоскость комплексной переменной z.

Рисунок 2.3. Область сходимости Z-преобразования единичного скачка

Уравнение окружности единичного радиуса с центром в начале координат определяется соотношением Неравенствусоответствует заштрихованная часть комплексной плоскости, в которой существует прямоеZ-преобразование единичного скачка. Радиус окружности, определяющей границу области существования прямогоZ-преобразования, называется радиусом сходимостиZ-преобразования. Для единичного скачка радиус сходимости равен единице.

Пример 3. Показательная функция

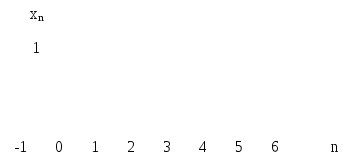
Рисунок 2.4. Показательная функция

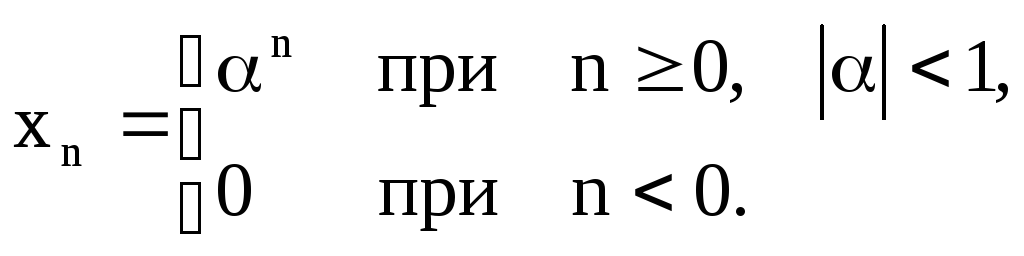
Радиус сходимости Z-преобразования показательной функции равен

Пример 4. Синусоида

Рисунок 2.5. Синусоида

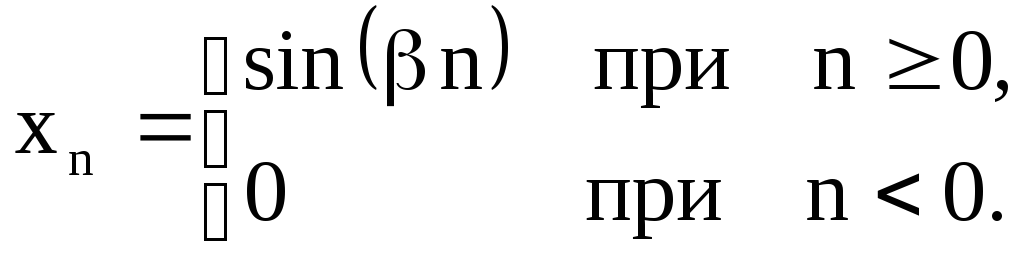
Входящие в последнее соотношение иприпредставляют собой суммы членов бесконечно убывающих геометрических прогрессий с первыми членами, равными единице и знаменателямиисоответственно.

Соотношение (2.1) определяет одностороннее прямое Z– преобразование. Наряду с односторонним существует двухстороннееZ– преобразование, в котором суммирование начинается не от нуля, а от.

Рассмотрим основные свойства прямого Z-преобразования.

1.Линейность. Пусть последовательность y_nпредставляет взвешенную сумму двух последовательностейx_1nиx_{2 n}

,

где постоянные весовые коэффициенты.

Воспользовавшись (2.1), найдём Z-преобразование последовательностиy_n

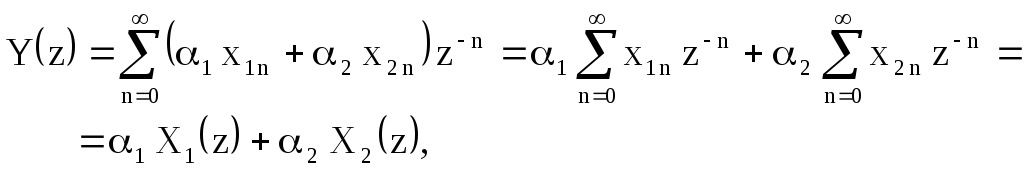.(2.2)

где -Z-преобразование последовательности

-Z-преобразование последовательности

Таким образом, Z-преобразование взвешенной суммы двух последовательностей равно взвешенной суммеZ-преобразований этих последовательностей.

Очевидно, что свойство линейности распространяется на любое число слагаемых в последовательности

2.Сдвиг последовательностей. Пусть последовательность y_n представляет собой сдвинутую (задержанную) на m отсчетов последовательность x_n

.

Рассмотрим случай, когда все члены последовательности с отрицательными индексами равны нулю (рисунок 2.6)

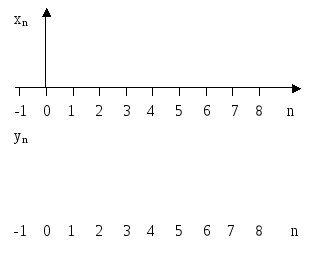
Рисунок 2.6 – Последовательность y_nсдвинута относительноx_n

на 2 отсчета (2 интервала дискретизации)

Определим Z-преобразование последовательности

Обозначим и перепишем последнее соотношение

(2.3)

Поскольку члены исходной последовательности с отрицательными индексами равны нулю, то первое слагаемое в (2.3) равно нулю.

Тогда Z-преобразование Y(z) последовательности y_n выражается через Z-преобразование X(z) последовательности x_n следующим образом

. (2.4)

Таким образом, Z-преобразование последовательности, задержанной относительно исходной на m отсчетов, равно Z-преобразованию исходной последовательности, умноженной на z ^–m.

3.Дискретная свертка двух последовательностей. Дискретной сверткой двух последовательностей x_n и h_n называется последовательность y_n, определяемая следующим соотношением

. (2.5)

Определим Z-преобразование дискретной свёртки

Поскольку при отсчёт последовательности, то внутренняя сумма не изменится, если её верхний предел n заменить на бесконечность.

Обозначим , вынесемза знак внутренней суммы и перейдём к суммированию по m, заменив нижний предел внешней суммы на В результате получим

В последнем соотношении учтено, что члены последовательности с отрицательными индексами равны нулю, следовательно, сумма от m=-k не отличается от суммы от m=0.

Полученное соотношение показывает, что Z-преобразование Y(z) дискретной свертки y_n двух последовательностей равно произведению Z -преобразований H(z) и X(z) исходных последовательностей h_n и x_n

, (2.6)

где .

2.2. Обратное Z-преобразование

Обратное Z-преобразование позволяет определить последовательность отсчётов дискретного сигнала по его прямому Z-преобразованию

Для определения обратного Z-преобразования найдём интеграл функции комплексного переменного, используя в качестве контура интегрированияокружность в плоскости комплексного переменногоzс центром в начале координат и выражение для прямогоZ-преобразования (2.1), заменив в нём индекс суммированияnнаk

В теории функций комплексного переменного доказывается, что интеграл от функции равенприпри всех остальных значенияхkон равен нулю. Поэтому из последнего соотношения получим

(2.7)

Если прямое Z-преобразование представлено полиномомгдеM-целое положительное число, то на основании определения прямогоZ-преобразования (2.1)n– ый член последовательности отсчётов дискретного сигналаx_nявляется коэффициентом приПоследовательность конечна, она содержитM+1 член.

Пример 1. ПрямоеZ-преобразование последовательности отсчетовx_nопределяется соотношением

Требуется определить последовательность отсчётов дискретного сигнала

При первое слагаемое в выражении дляможно представить как, следовательно,. Коэффициенты прии2 и 1 соответственно. Поэтому

Во всех других случаях для определения нужно воспользоваться (2.7).

Введём обозначение подинтегральной функции комплексного переменного в (2.7)

Функции комплексного переменного характеризуются полюсами и нулями.

Полюсом функции называется значение комплексного переменногоz, при котором функциястремится к бесконечности.

Нулём функции называется значение комплексного переменногоz, при котором функциястремится к нулю.

В теории функций комплексного переменного доказывается теорема о вычетах. Интеграл от функции , взятый по замкнутому контуру, содержащемуся в области, где функция является однозначной и аналитической, за исключением особых точек однозначного характера, и не проходящему через особые точки, равен произведению суммы вычетов функции относительно всех особых точек, заключённых внутри, на.

Вычетом функции относительно изолированной особой точки а однозначного характера называется коэффициент прив лорановском разложении функции в окрестности точкиа.

Пусть а – простой полюс функции. Тогда в окрестности точкиа имеет место разложение в ряд Лорана

Умножим левую и правую часть последнего соотношения на

Из последнего соотношения следует

Вычисление вычета упрощается, если можно представить в виде отношения двух функций комплексного переменного

где т.е. имеет простой нуль при

Следовательно, имеет простой полюс при.

Найдём вычет

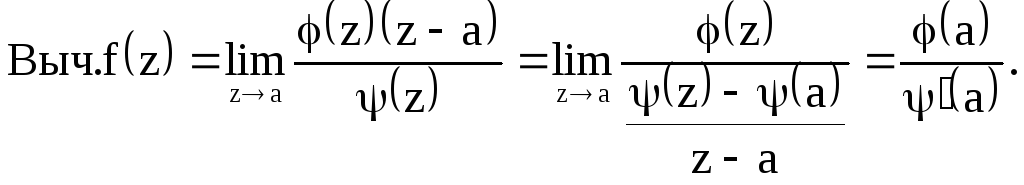(2.8)

Пример 2. Z-преобразование последовательностиопределяется соотношением

Требуется найти последовательность x_n

Подинтегральная функция определяется следующим соотношением

Из последнего соотношения следует, что

Нуль функции (полюс функции) находится из уравненияи равенпоэтому

В результате получим

Если функция имеет более одного полюса, то её нужно представить в виде суммы функций, имеющих только один полюс и применить к каждому слагаемому этой суммы соотношение (2.8).

Пример 2. Z-преобразование последовательностиопределяется соотношением

Требуется найти последовательность x_n

Функция определяется следующим соотношением

Преобразуем дробь, входящую в последнее соотношение

(2.9)

где QиP– коэффициенты, которые следует определить.

Для определения коэффициента Qумножим левую и правую части последнего соотношения наи найдём пределы левой и правой части уравнения при

Для определения коэффициента Pумножим левую и правую (2.9) наи найдём пределы левой и правой части уравнения при

Представим функцию с учётом соотношений дляQиP

Определим последовательность отсчетов дискретного сигнала

Рассмотрим случай кратных полюсов. Пусть a– полюс кратностиk. Тогда в окрестности точкиaсправедливо разложение в ряд Лорана

Умножим левую и правую части последнего соотношения на получим

Для определения a_-1продифференцируем последнее соотношение почленнораз

При получим

. (2.10)

Пример 3. Z-преобразование последовательностиопределяется соотношением

Требуется найти последовательность

Функция определяется следующим соотношением

При k=2 по (2.10) найдем

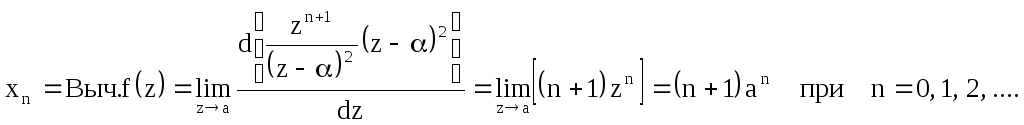
2.3. Дискретные линейные системы, их свойства и характеристики

В зависимости от вида обрабатываемых сигналов системы обработки подразделяются на аналоговые, дискретные и цифровые. Дискретные системы осуществляют обработку дискретных сигналов.

Дискретные системы могут быть линейными и нелинейными.

На рисунке 2.7 представлена линейная дискретная система в самом общем виде. У неё есть вход, на котором действует последовательность отсчетов и выход, на котором действует последовательность отсчетов

Рисунок 2.7. Общее представление дискретной линейной системы

Линейной называется система, которая удовлетворяет принципу суперпозиции или наложения. Сущность принципа суперпозиции: реакция системы на сумму воздействий равна сумме реакций на каждое воздействии в отдельности.

Поясним принцип суперпозиции применительно к дискретной линейной системе. Пусть при действии на входе сигнала на выходе дискретной системы появляется сигнала входному сигналусоответствует сигнал

Дискретную систему можно считать линейной, если при входном сигнале на выходе системы будет действовать сигнал

Из принципа суперпозиции вытекает и другое важное свойство линейной системы: пропорциональность. Свойство пропорциональности означает, что входному сигналу

соответствует сигналгде- постоянные коэффициенты.

Линейная дискретная система является инвариантной во времени, если задержка во времени входного сигнала вызывает такую же задержку выходного сигнала.

Пусть дискретному сигналу соответствует сигналЕсли система является инвариантной во времени, то сигналусоответствует сигнал

Принцип инвариантности иллюстрируется рисунком 2.8. Из рисунка видно, что входной сигнал сдвинут относительно входного сигналана 2 отсчёта. При этом выходной сигналсдвинут относительно выходного сигналатакже на 2 отсчета.

Рассмотрим основные характеристики линейной дискретной системы.

Импульсной характеристикойдискретной линейной системы называется выходной сигнал системы при действии на её входе единичного отсчёта и при нулевых начальных условиях (рисунок 2.9). На рисунке 2.9 и в дальнейшем импульсная характеристика будет обозначаться

Рисунок 2.8. Иллюстрация принципа инвариантности

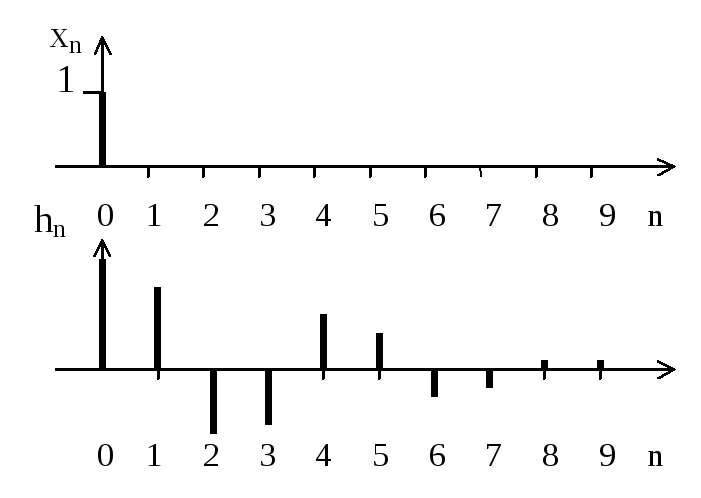
Рисунок 2.9 – Единичный отсчет x_n и импульсная характеристика h_n

Импульсная характеристика может быть конечной или бесконечной, может быть затухающей или возрастающей.

Системной (передаточной) функцией линейной дискретной системы называется отношение Z-преобразования выходного сигнала к Z-преобразованию входного сигнала при нулевых начальных условиях

(2.11)

где

Полюсомсистемной функции называется значение комплексной переменнойz, при котором системная функция устремляется к бесконечности.

Нулёмсистемной функции называется значение комплексной переменнойz, при котором системная функция равна нулю.

Комплексным коэффициентом передачилинейной дискретной системы называется отношение комплексной амплитуды выходного синусоидального сигналак комплексной амплитуде входного синусоидального сигнала

где амплитуды выходного и входного сигналов соответственно,начальные фазы выходного и входного сигналов соответственно.

Поэтому комплексный коэффициент передачи равен

где коэффициент передачи, равный модулю комплексного коэффициента передачи и представляющий собой отношение амплитуды выходного синусоидального сигнала к амплитуде входного синусоидального сигнала,аргумент комплексного коэффициента передачи, который показывает, какой фазовый сдвиг приобретает входной синусоидальный сигнал при прохождении через линейную дискретную систему.

Частотной характеристикойлинейной дискретной системы называется зависимость комплексного коэффициента передачи от частоты

где - круговая частота,- зависимость коэффициента передачи (модуля комплексного коэффициента передачи) от частоты,- зависимость фазового сдвига, вносимого линейной дискретной системой, (аргумента комплексного коэффициента передачи) от частоты.

Зависимость коэффициента передачи от частоты называетсяамплитудно-частотной характеристикой (АЧХ)линейной дискретной системы.

Зависимость фазового сдвига, вносимого линейной дискретной системой от частоты называетсяфазочастотной характеристикой (ФЧХ).

В этом подразделе даны определения основных характеристик линейных дискретных систем. В дальнейшем эти характеристики будут рассмотрены подробно.

2.4. Определение выходного сигнала линейной инвариантной относительно сдвига

дискретной системы по входному сигналу и импульсной характеристике

Определение выходного сигнала линейной инвариантной относительно сдвига дискретной системы по входному сигналу и импульсной характеристике основано на определении импульсной характеристики, принципе суперпозиции, свойстве пропорциональности и инвариантности системы относительно сдвига.

На рисунке 2.10 приведен пример определения выходного сигнала в случае, когда входной сигнал x_n содержит два отсчета x₀ = 2 и x₁= 2, а импульсная характеристика 4 отсчета: h₀ = 1, h₁=0.8, h₂ = 0.5, h₃ = 0.3.

Сначала определим реакцию фильтра на отсчет x₀, считая, чтоx₁=0. Если бы вместоx₀действовал единичный отсчет, то выходным сигналом была бы импульсная характеристика. Однако x₀= 2, поэтому на основании свойства пропорциональности реакцией системы на нулевой входной отсчёт будет импульсная характеристика, все отсчёты которой умножаются наx₀.

Определим реакцию фильтра на отсчёт x₁, считая, что отсчётx₀отсутствует. Если бы на месте отсчётаx₁был единичный отсчёт, то выходным сигналом системы была бы импульсная характеристика, которая из-за инвариантности системы относительно сдвига начиналась бы приn=1. Посколькуто реакцией системы наx₁ является импульсная характеристика с началом приn=1, все отсчёты которой умножаются наx₁.

Следующим шагом является суммирование полученных реакций при каждом значении порядкового номера отсчёта n. В результате получим:

,, …

В общем случае

(2.12)

Согласно последнему соотношению

Рисунок 2.10. Определение выходного сигнала по входному сигналу

и импульсной характеристике

Однако в рассмотренном примере x₂= 0, поэтому, как видно из рисунка,

В общем случае

В данном примере x₂=x₃= 0, поэтому

В общем случае

В рассматриваемом случае т.к.x₂=x₃=x₄ = 0 иh₄=0.

Соотношение 2.12 представляет собой дискретную свертку последовательностей x_nиh_n, т.е.выходной сигнал линейной инвариантной во времени дискретной системы представляет собой дискретную свертку входного сигнала и импульсной характеристики.

На рисунке 2.11 представлен графический способ нахождения дискретной свёртки двух последовательностей конечной длины: импульсной характеристики h={1,1}, и входного сигналаx={3, 2, 1}.

Рисунок 2.11. Графический способ определения дискретной свёртки

Текущий отсчет дискретной свёртки определяется с учётом взаимного расположения на рисунке двух последовательностей h_kиx_n-k (2.12) как сумма произведений взаимно перекрывающихся во времени отсчётов этих последовательностей.

В позиции 1 приведено взаимное расположение последовательностейh_kиx_0-kдля определения нулевого отсчёта дискретной свёртки

В позиции 2приведено взаимное расположение последовательностейh_kиx_1-kдля определения первого отсчёта дискретной свёртки

Позиции 3 и 4 иллюстрируют вычисление второгоy₂и третьегоy₃отсчётов дискретной свёртки.

При конечной импульсной характеристике, содержащей Nотсчётов, соотношение (2.12) преобразуется к виду

,(2.13)

На рисунке 2.12 дано графическое представление соотношения (2.13), которое условно называют структурной схемой линейной дискретной системы с конечной импульсной характеристикой.

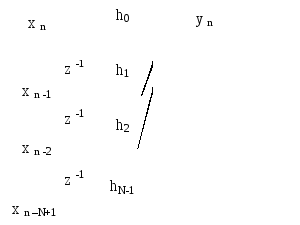
Рисунок 2.12. Структурная схема линейной дискретной системы с конечной

импульсной характеристикой

2.5. Разностное уравнение и системная функция дискретной линейной системы. Связь

между системной функцией и импульсной характеристикой

В линейной дискретной системе текущий n– ый отсчёт выходного сигнала в общем случае связан линейными зависимостями с текущим и предыдущими отсчетами входного сигналаx_n,x_n-1,x_n-2.. и с предыдущими отсчётами выходного сигналаy_n-1,y_n-2, ..

(2.14)

Соотношение (2.14) называется разностным уравнением линейной дискретной системы. По характеру зависимости текущего отсчёта выходного сигнала y_nот отсчётов входного и выходного сигналов дискретные линейные системы подразделяются на рекурсивные и нерекурсивные.

Если n-ый отсчет выходного сигнала y_n зависит только от отсчетов входного сигнала в данный и предшествующие моменты дискретного времени x_n, x_n-1 ..и т.д., то такая линейная дискретная система называется нерекурсивной.

У нерекурсивной системы все N коэффициентов A_k в разностном уравнении (2.14) равны нулю. Её структурная схема приведена на рисунке 2.12.

Если n-ый отсчет выходного сигнала y_n зависит не только от отсчетов входного сигнала в данный и предшествующие моменты дискретного времени x_n, x_n-1 ..и т.д., но и от отсчетов выходного сигнала в предшествующие моменты времени, то такая линейная дискретная система называется рекурсивной.

Нерекурсивная дискретная система является системой без обратных связей, а рекурсивная система – это система с обратными связями.

Найдём системную функцию линейной дискретной системы. Для этого, воспользовавшись свойствами прямого Z-преобразования, перейдём от разностного уравнения (2.14) к уравнению в Z-преобразованиях

Из последнего соотношения выразим Y(z) через X(z)

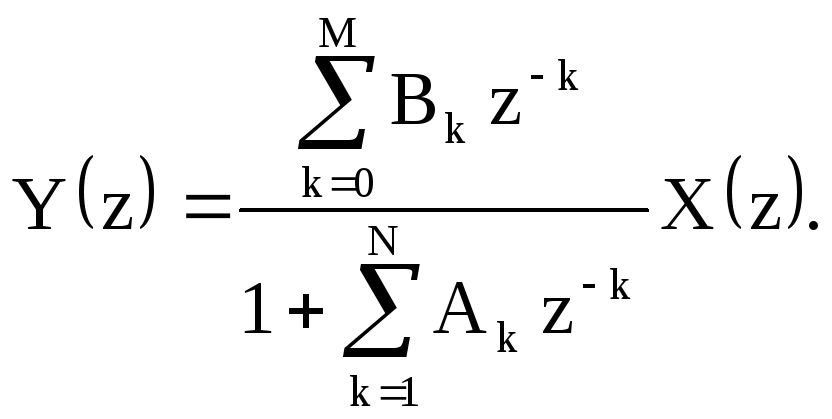
Разделив Y(z) на X(z), найдём системную функцию

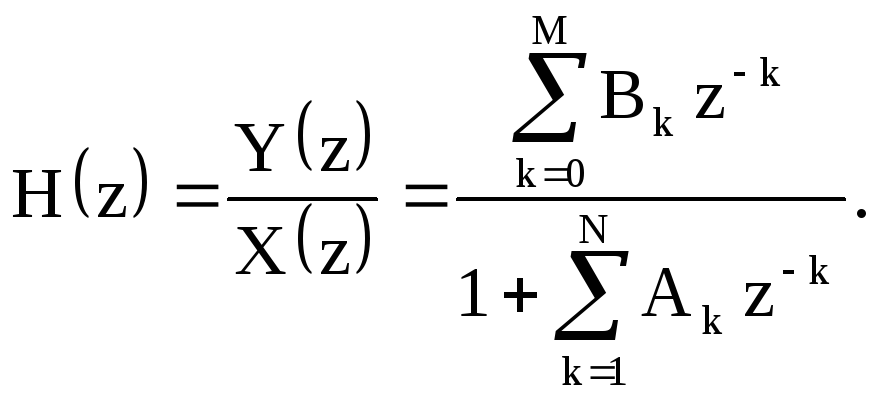(2.15)

В нерекурсивной дискретной линейной системе A_k=0 для всех значенийk, поэтому системная функция выражается полиномом относительно комплексного переменногоz^-1

Системная функция рекурсивной дискретной системы представляет собой дробно-рациональную функцию с полиномами относительно комплексного переменного z^-1 в числителе и знаменателе (2.15).

Отметим, что знаки перед коэффициентами A_kв выражении для системной функции и в разностном уравнении противоположны.

Чтобы найти нули системной функции, нужно полином числителя приравнять нулю и найти корни полученного уравнения.

Чтобы найти полюсы системной функции, нужно полином знаменателя приравнять нулю и найти корни полученного уравнения.

Пример.

Требуется определить нули и полюсы системной функции и привести карту нулей и полюсов – расположение нулей и полюсов на комплексной плоскости z

Для определения нулей найдём корни уравнения или

Для определения полюсов найдём корни уравнения или

Рисунок 2.13. Карта нулей и полюсов

Выясним, какая связь существует между системной функцией и импульсной характеристикой линейной дискретной системы.

В разделе 2.4 показано, что выходной сигнал линейной дискретной системы y_nпредставляет собой дискретную свёртку входного сигналаx_nи импульсной характеристикиh_n

Z-преобразование дискретной свёртки равно произведениюZ-преобразование свёртуемых последовательностей

,

где .

Из определения системной функции следует, что Z-преобразование выходного сигнала равно произведению системной функции наZ-преобразование входного сигнала.

Следовательно, входящее в последнее соотношение Z-преобразование импульсной характеристикиH(z) является системной функцией дискретной линейной системы.

Таким образом, системная функция является прямым Z-преобразованием импульсной характеристики, а значит, импульсная характеристика является обратнымZ-преобразованием системной функции.

2.6. Связь между комплексным коэффициентом передачи и системной функцией

дискретной линейной системы

Для определения комплексного коэффициента передачи дискретной линейной системы подадим на её вход комплексный сигнал (рисунок 2.14)

Рисунок 2.14. Дискретная линейная система с комплексными сигналами

на входе и выходе

Поскольку комплексный коэффициент передачи определяется как отношение комплексной амплитуды выходного сигнала к комплексной амплитуде входного синусоидального сигнала, то при амплитуде входного сигнала, равной единице, комплексная амплитуда выходного сигнала равна комплексному коэффициенту передачи

Поэтому выходной сигнал системы должен быть равен

С другой стороны выходной сигнал y_nсвязан с входным сигналомx_nразностным уравнением (2.14).

С учётом выражений для входного и выходного сигнала системы разностное уравнение преобразуется к виду

Разделим левую и правую части уравнения на общий множитель и учтём, чтоне зависит от индекса суммированияk. В результате получим

Из последнего соотношения найдём комплексный коэффициент передачи

В разделе 2.5 получено выражение для системной функции дискретной линейной системы

Сопоставление двух последних выражений показывает, что для определения комплексного коэффициента передачи достаточно в выражении для системной функции выполнить подстановку

(2.16)

Введём обозначение

где - нормированная частота.

Поэтому - нормированная круговая частота.

С учётом введённого обозначения перепишем (2.16)

(2.17)

Функция является периодической с периодом, равным частоте дискретизации. Поскольку, то зависимость комплексного коэффициента передачи от частоты также является периодической функцией с периодом, равным частоте дискретизации.

Пример

Определить комплексный коэффициент передачи линейной дискретной системы на частоте, равной четверти частоты дискретизации, если системная функция определяется соотношением

В выражении для системной функции заменяем zна

Определим значение на частоте, равной четверти частоты дискретизации

Подставляя значение в выражение для комплексного коэффициента передачи, получим

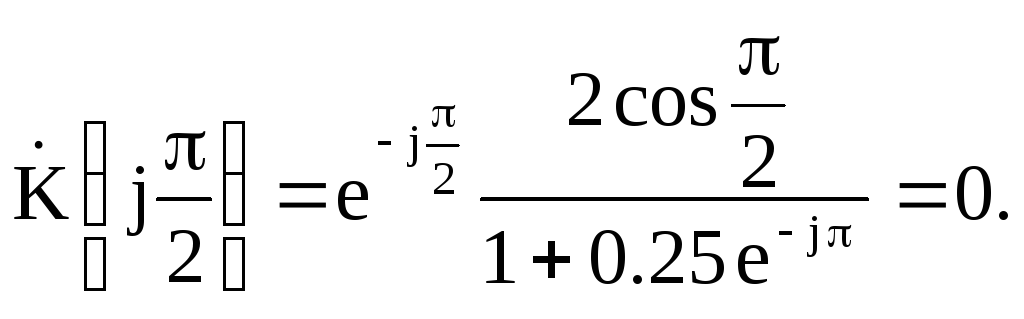
2.7. Устойчивость линейной дискретной системы

Рассмотрим критерии устойчивости цифровых линейных дискретных систем.

1.Критерий «ОВ-ОВ» («Ограниченный вход – ограниченный выход»)

Линейная дискретная система устойчива, если при ограниченном входном сигнале выходной сигнал системы также ограничен.

Условие ограниченности входного сигнала определяется соотношением , где, а условием ограниченности выходного сигнала является.

Непосредственное использование этого критерия весьма затруднительно, т.к. требует определения значений отсчетов выходного сигнала при всех возможных значениях отсчетов входного сигнала. Поэтому требуются критерии, позволяющие оценить устойчивость системы на основании её характеристик.

2. Критерий оценки устойчивости по импульсной характеристике

В разделе 2.4 было доказано, что выходной сигнал линейной дискретной системы представляет собой дискретную свертку входного сигнала и её импульсной характеристики.

.

Абсолютное значения отсчетов выходного сигнала удовлетворяет неравенству

.

При справедливо неравенство

.

Следовательно,

.

Таким образом, чтобы обеспечить выполнение условия , достаточно выполнить условие

. (2.18)

Последнее соотношение определяет критерий устойчивости, который формулируется так: линейная дискретная система устойчива, если сумма абсолютных значений отсчетов её импульсной характеристики конечна.

Из этого критерия следует, что все системы с конечной импульсной характеристикой абсолютно устойчивы.

Пример 1

Требуется проверить устойчивость линейной дискретной системы, импульсная характеристика которой бесконечна и описывается соотношением

,

где – положительная константа, от которой зависит скорость убывания отсчетов импульсной характеристики.

Учитывая, что и воспользовавшись соотношением для определения суммы членов бесконечно убывающей геометрической прогрессии, получим

.

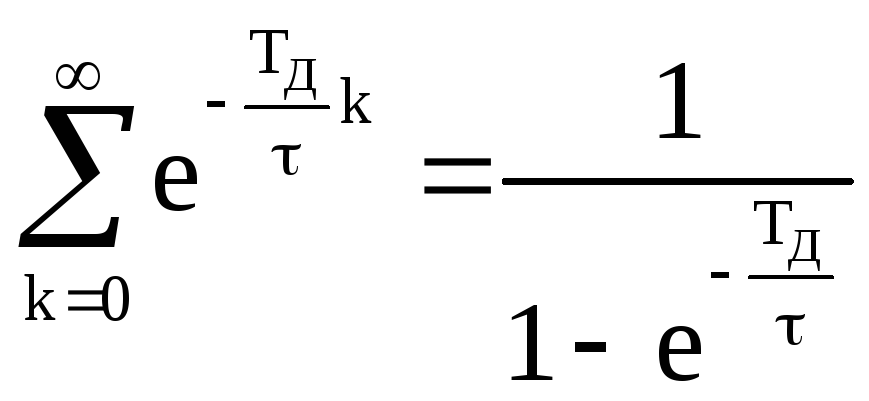Так как , то фильтр устойчив.

3. Критерий оценки устойчивости по системной функции

В разделе 2.5 показано, что системная функция представляет собой Z-преобразование импульсной характеристики линейной дискретной системы

.

Модуль системной функции удовлетворяет неравенству

.

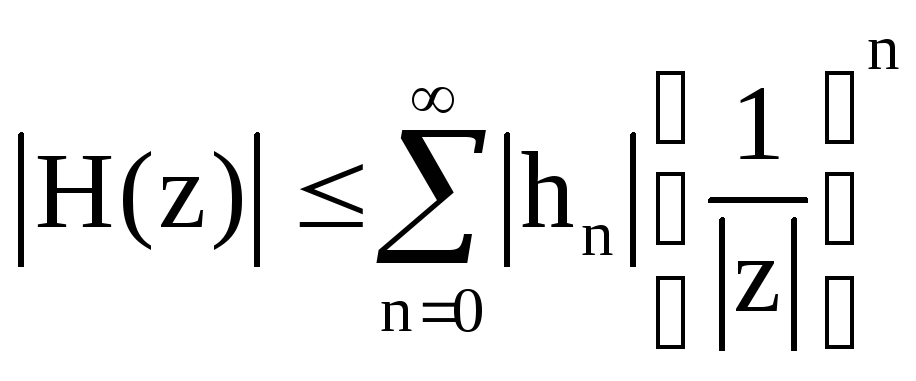При справедливо неравенство

.

При и примодуль системной функции. Последнее соотношение означает, что в устойчивой линейной дискретной системе должны отсутствовать полюсы системной функции в области комплексной переменнойz, которая удовлетворяет неравенству.

Следовательно, если полюсы существуют, то в устойчивой системе они должны располагаться в области комплексной плоскости, для которой выполняется условие .

Поэтому критерий устойчивости, связанный с системной функцией, формулируется следующим образом: линейная дискретная система устойчива, если полюсы системной функции располагаются внутри круга единичного радиуса с центром в начале координат ().

Пример 2

Требуется оценить устойчивость линейной дискретной системы, системная функция которой описывается соотношением

где A₁= - 0.5,A₂= 1.2.

Приравняем знаменатель системной функции нулю и определим корни полученного уравнения, которые являются координатами полюсов

.или

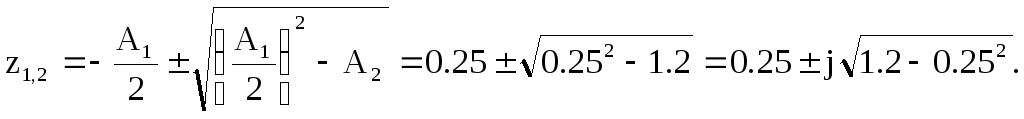
Так как , то полюсы системной функции располагается вне круга единичного радиуса. Следовательно, система не устойчива.

2.8. Классификация и формы программной реализации цифровых фильтров

Если линейная дискретная система обладает свойством частотной избирательности, т.е. пропускает колебания одних частот и задерживает колебания других частот, то она является дискретным фильтром. Однако практическая реализация дискретного фильтра потребовала бы использования вычислительных устройств неограниченной разрядности, т.к. сигналы дискретного фильтра являются произвольными по величине.

Поскольку разрядность реальных вычислительных устройств ограничена, то в них могут существовать только цифровые сигналы – квантованные по уровню дискретные сигналы. Соответственно система обработки этих сигналов является цифровой, в которой нужно учитывать погрешности вычислений, отсутствующие в дискретной системе.

Временная зависимость ошибок квантования дискретного сигнала называется шумом квантования. Шум квантования сопровождает входной сигнал цифровой системы, а также возникает в самой системе из-за округления результатов вычислений. Последнее создаёт нелинейные эффекты в линейной системе.

Наличие шумов квантования отличает цифровой фильтр от дискретного фильтра. Поскольку современные вычислительные устройства обладают высокой разрядностью, то в них можно обеспечить низкий уровень шумов квантования, следовательно, считать цифровой фильтр линейной системой.

Цифровым фильтром называется линейная частотно-избирательная линейная система, реализуемая на основе вычислительного устройства.

Все выводы и определения, относящиеся к линейной дискретной системе, справедливы для цифрового фильтра.

Рассмотрим классификацию цифровых фильтров.

По диапазону частот сигналов, пропускаемых на выход, фильтры подразделяются на

• фильтры нижних частот (ФНЧ),

• фильтры верхних частот (ФВЧ),

• полосовые фильтры (ПФ),

• режекторные фильтры (РФ).

На рисунке 2.15 приведены идеальные АЧХ этих фильтров в интервале от нуля до половины частоты дискретизации.

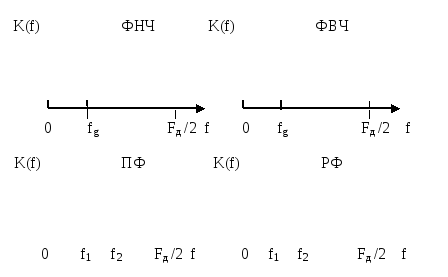
Рисунок 2.15. АЧХ четырёх типов цифровых фильтров

Из рисунка видно, что у ФНЧ полоса пропускания находится в интервале от нуля до граничной частоты f_g, а частота задерживания в интервале отf_gдоF_д /2.

У ФВЧ полоса пропускания в интервале от граничной частоты f_gдоF_д /2, а полоса задерживания в интервале от нуля доf_g.

Полосовой фильтр имеет одну полосу пропускания от f₁доf₂и две полосы задерживания: левая полоса задерживания от нуля доf₁, правая полоса задерживания отf₂доF_д /2.

Режекторный фильтр имеет одну полосу задерживания от f₁доf₂и две полосы пропускания: левую от нуля доf₁и правую отf₂доF_д /2.

У реальных цифровых фильтров, как и у аналоговых, существует переходная полоса между полосой пропускания и полосой задерживания.

По характеру зависимости текущего отсчёта выходного сигнала y_nот отсчётов входного и выходного сигналов цифровые фильтры подразделяются на

• нерекурсивные фильтры и

• рекурсивные фильтры.

Определения рекурсивных и нерекурсивных фильтров соответствуют определениям рекурсивных и нерекурсивных линейных дискретных систем, которые даны в разделе 2.5.

По виду импульсной характеристики цифровые фильтры подразделяются на

• КИХ - фильтры (фильтры с конечной импульсной характеристикой) и

• БИХ – фильтры ( фильтры с бесконечной импульсной характеристикой).

Рассмотрим формы программной реализации цифровых фильтров.

1.Прямая форма.

Прямая форма программной реализации цифрового фильтра – это программирование разностного уравнения линейной дискретной системы

На рисунке 2.16 приведена структурная схема цифрового фильтра при прямой форме реализации – графическое представление разностного уравнения

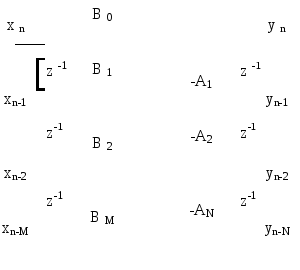
Рисунок 2.16 – Прямая форма программной реализации фильтра

В разделе 2.5 было показано, что разностному уравнению линейной дискретной системы соответствует системная функция

В фильтре рисунка 2.16 текущий отсчет выходного сигнала y_nзависит как от отсчётов входного сигнала, так и отсчётов выходного сигналаследовательно, этот фильтр является рекурсивным. При равенстве нулю всех коэффициентовон становится нерекурсивным.

2. Каноническая форма

Представим системную функцию H(z) в виде произведения двух функций

,

где

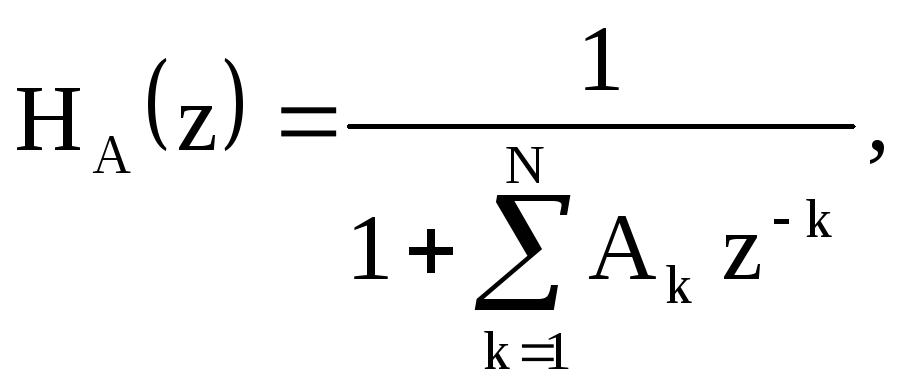
Согласно последнему соотношению цифровой фильтр с системной функцией H(z) можно представить в виде последовательного соединения двух фильтров с системными функциямиH_A(z) иH_B(z) (рисунок 2.17).

Рисунок 2.17 – Представление фильтра с прямой формой реализации

в виде последовательного соединения двух фильтров

Действительно,

.

После детализации укрупнённых блоков рисунка 2.17 получим схему, представленную на рисунке 2.18

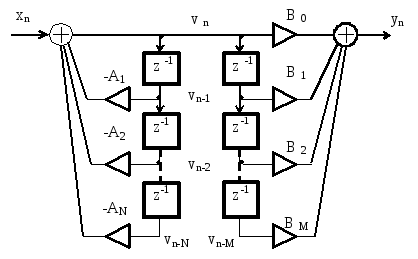
Рисунок 2.18 – Детальный алгоритм представления фильтра с прямой реализацией