
Материалы по мат. анализу для самостоятельного обучения / Тесты к главе 3
.doc
Вариант 1
-
Вычислить двойной интеграл
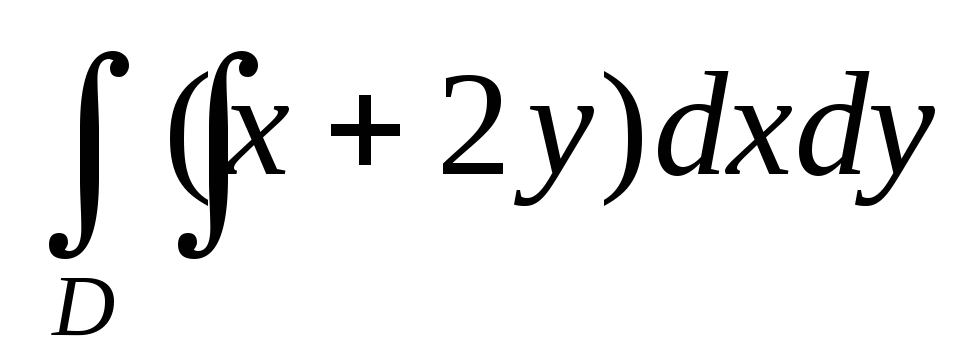 по прямоугольной области D
(
по прямоугольной области D
(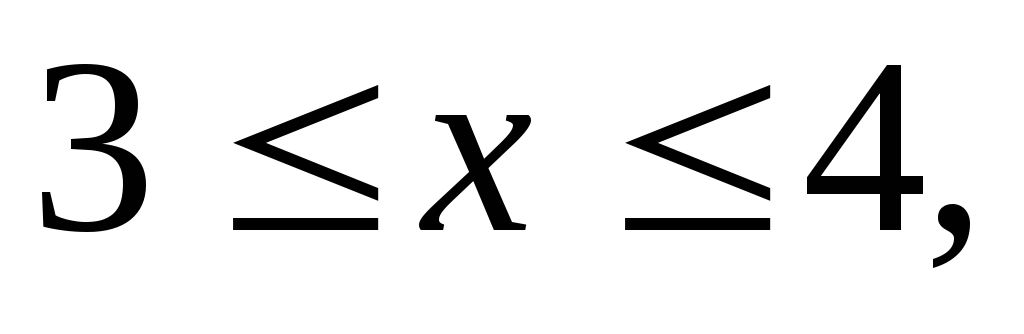
 ).
).
а)![]() б)
б)
![]() в)
в)![]() , г)0.
, г)0.
-
Вычислить двойной интеграл:
 где область D
ограничена кривыми
где область D
ограничена кривыми
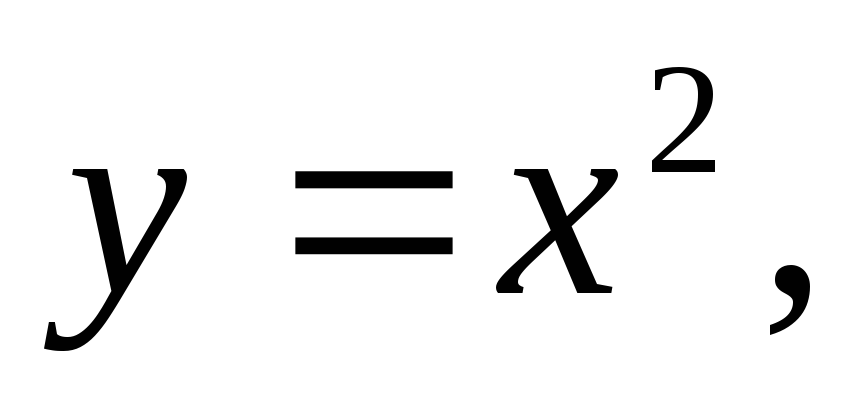
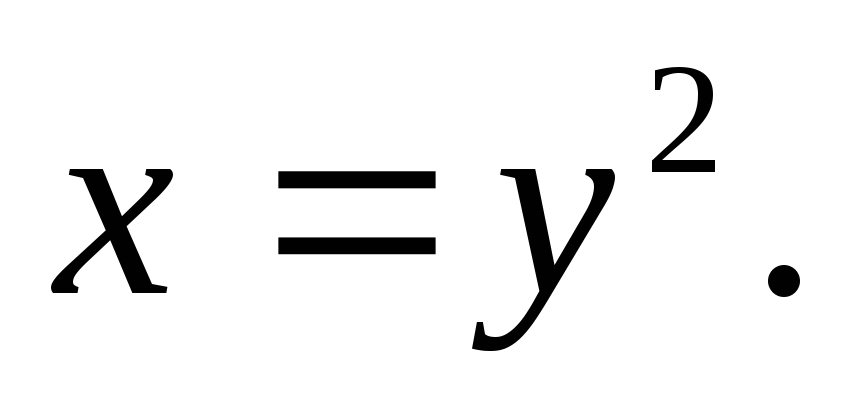
а)![]() б)
б)
![]() в)
в)
![]() г)
г)
![]()
-
Вычислить двойной интеграл, переходя к полярным координатам:
 где область D
- круг
где область D
- круг
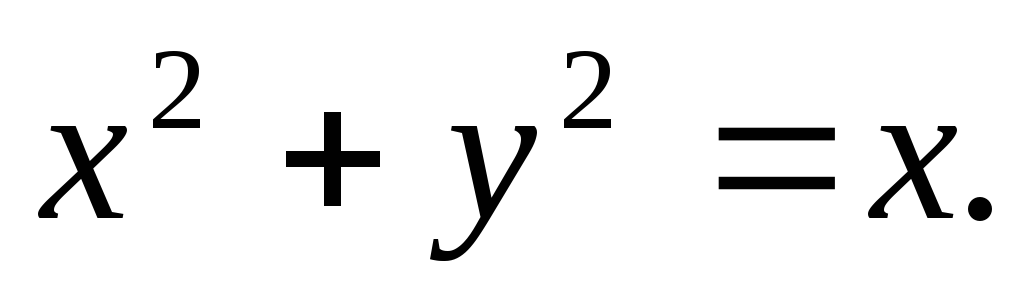
а)
![]() б)
б)
![]() в)
в)
![]() г)
г)
![]()
-
Найти площадь, ограниченную кривыми:
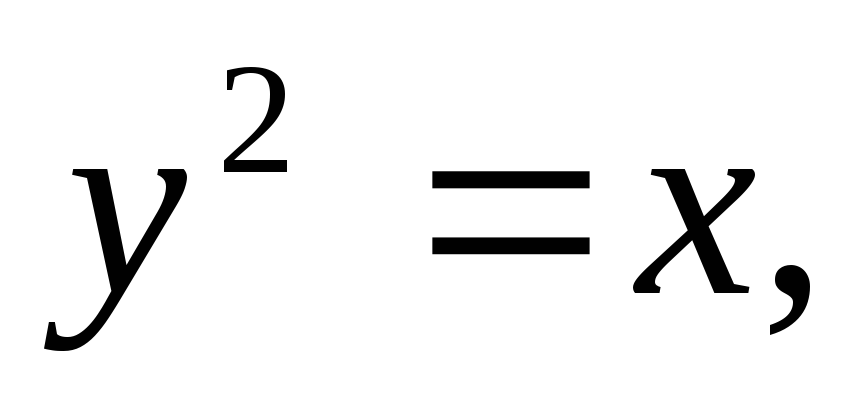

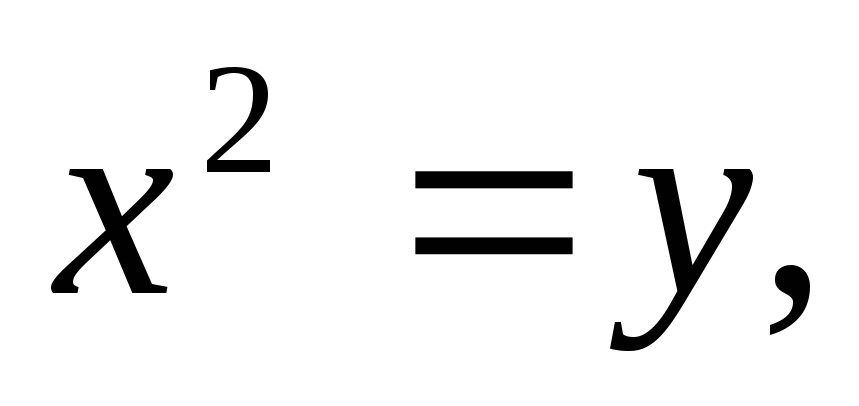
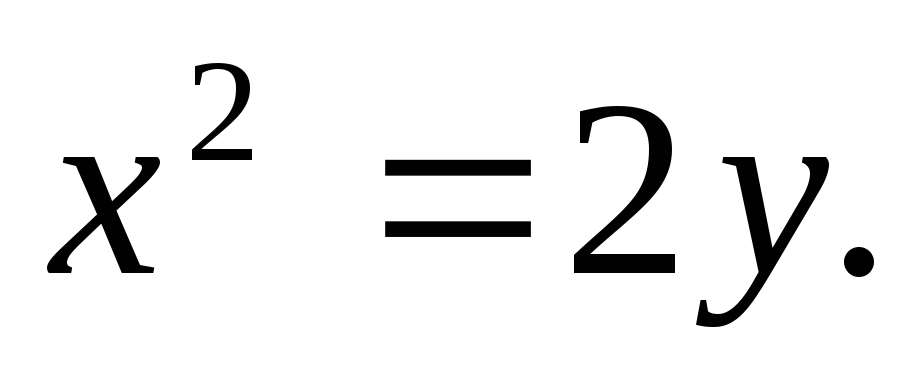
а)![]() б)
б)
![]() в)
в)
![]() г)
г)
![]()
-
Вычислить тройной интеграл:
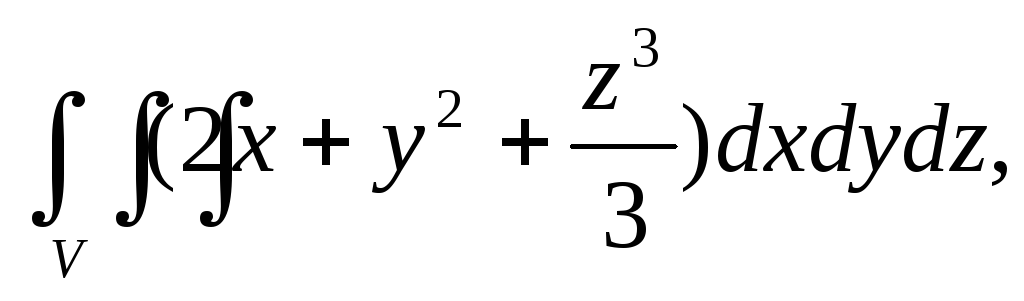 где область V
– прямоугольный параллелепипед (
где область V
– прямоугольный параллелепипед (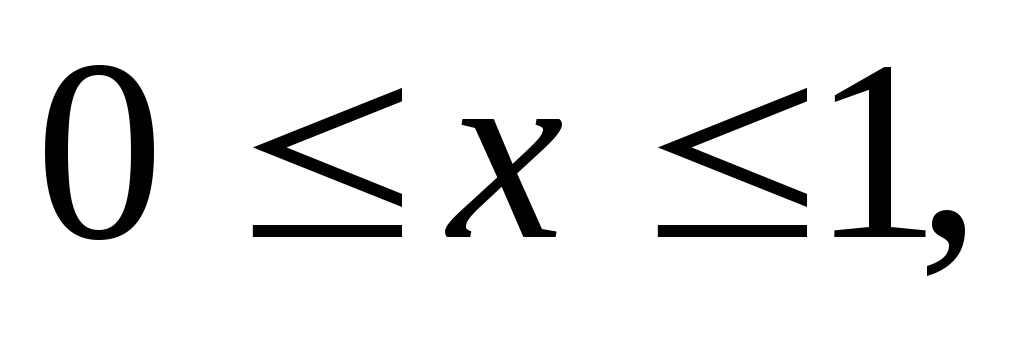
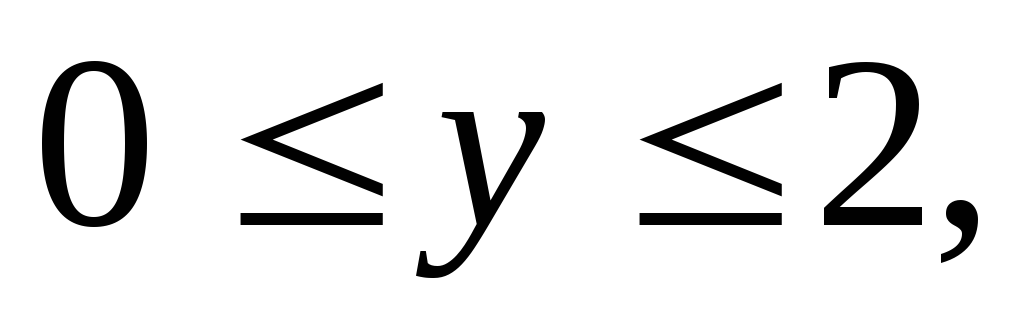
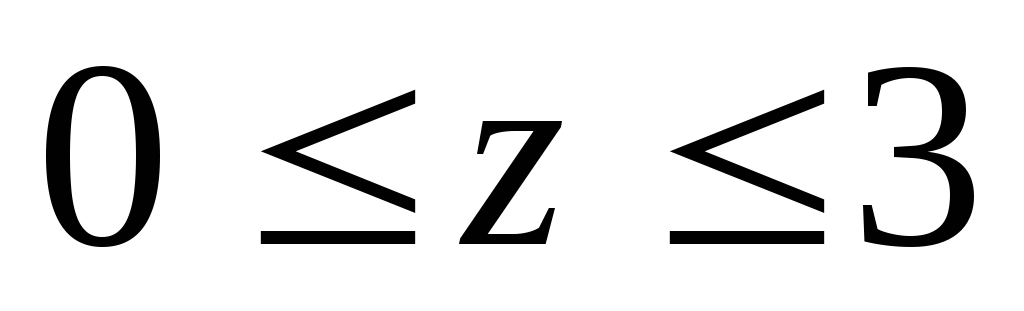 ).
).
а)27,5, б)33,5, в)62, г)26,5.
-
Вычислить тройной интеграл:
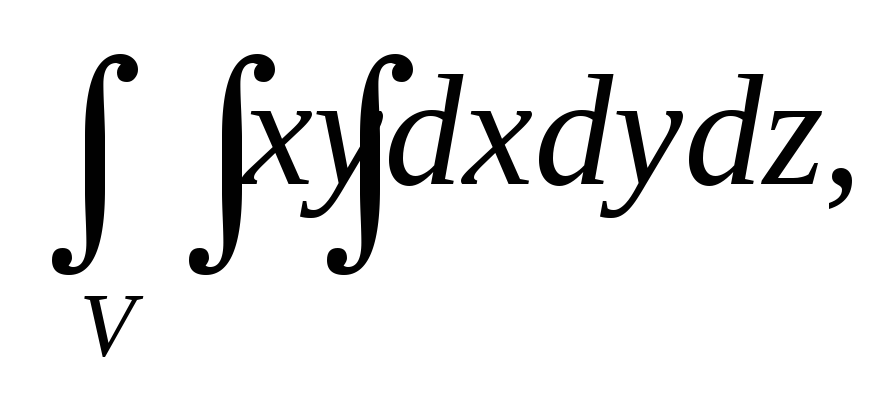 где область V
задается неравенствами
где область V
задается неравенствами
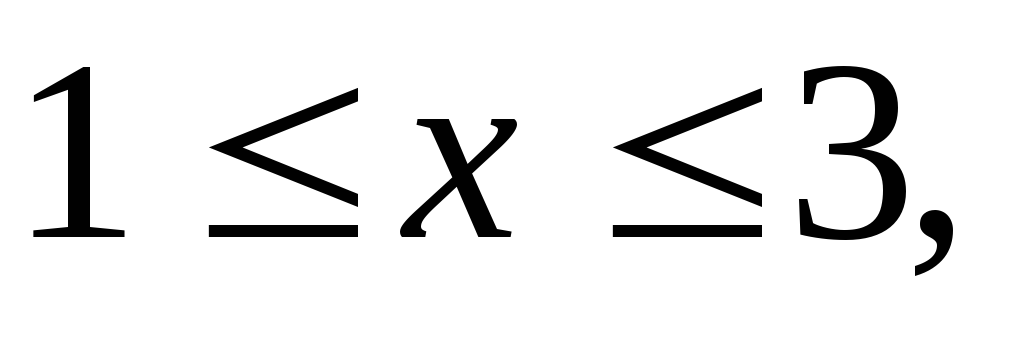


а) 26, б)13, в)7, г)14.
Вариант 2
-
Вычислить двойной интеграл:
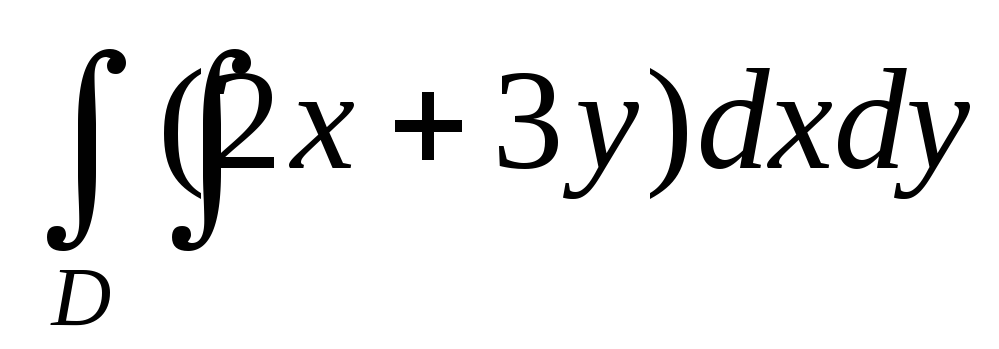 ,
,
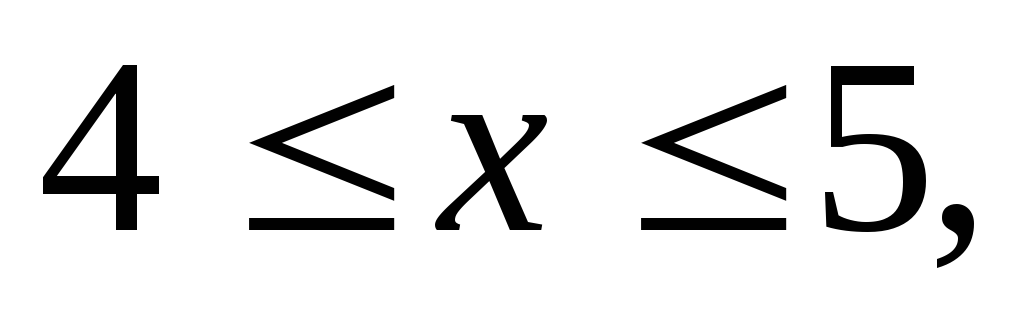
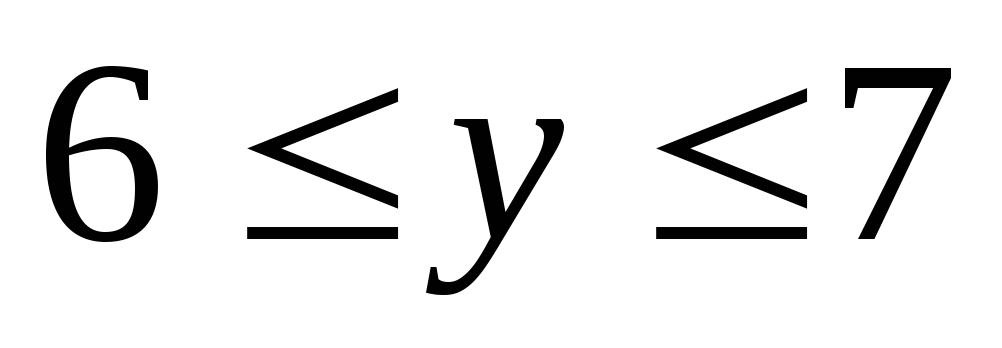 .
.
а)![]() б)
б)
![]() в)
в)
![]() г)
г)
![]()
-
Вычислить двойной интеграл:
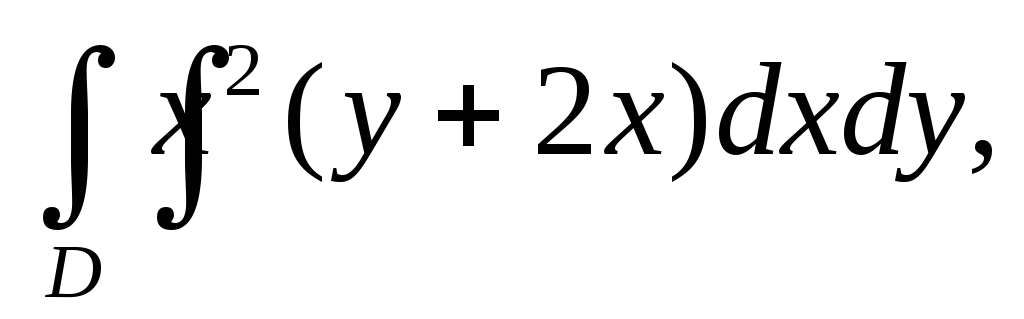

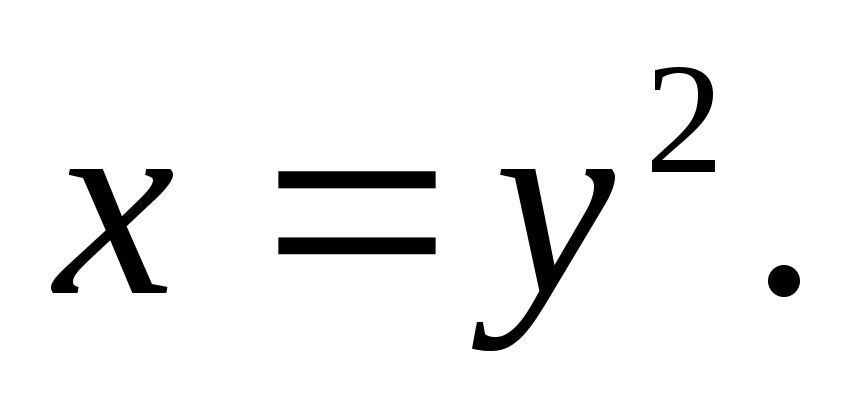
а)![]() б)
б)
![]() в)
в)
![]() г)
г)
![]()
-
Вычислить двойной интеграл, переходя к полярным координатам:
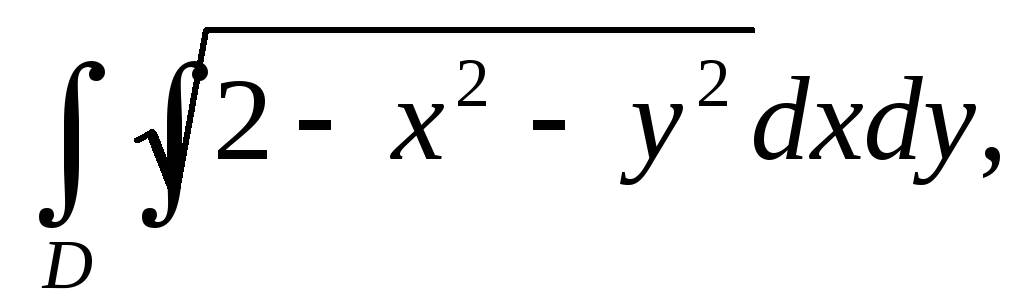
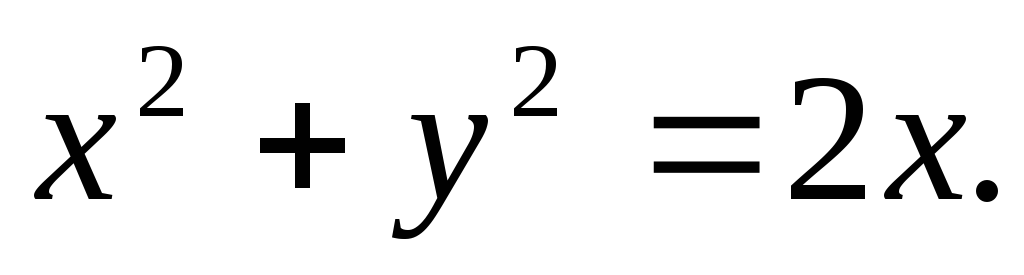
а)
![]() б)
б)
![]() в)
в)
![]() г)
г)
![]()
-
Найти площадь, ограниченную кривыми:

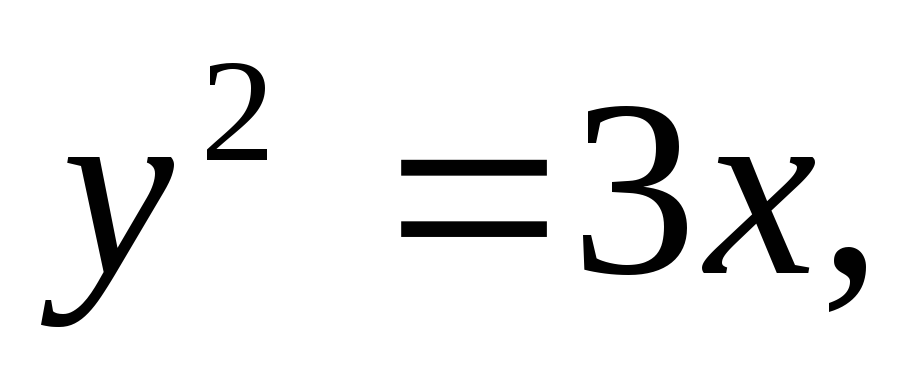
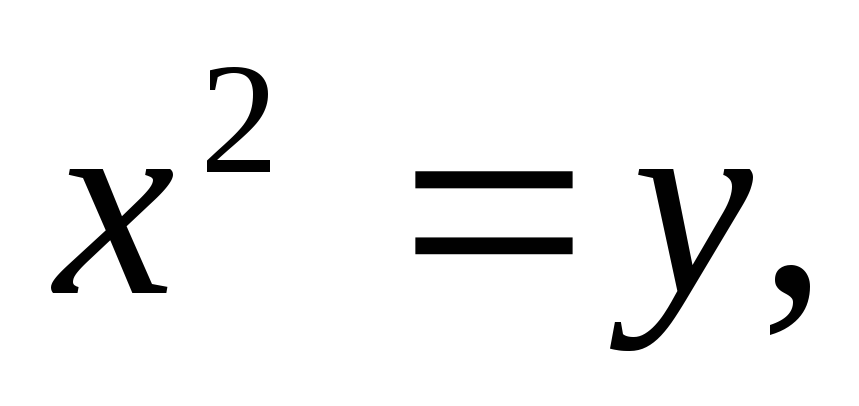
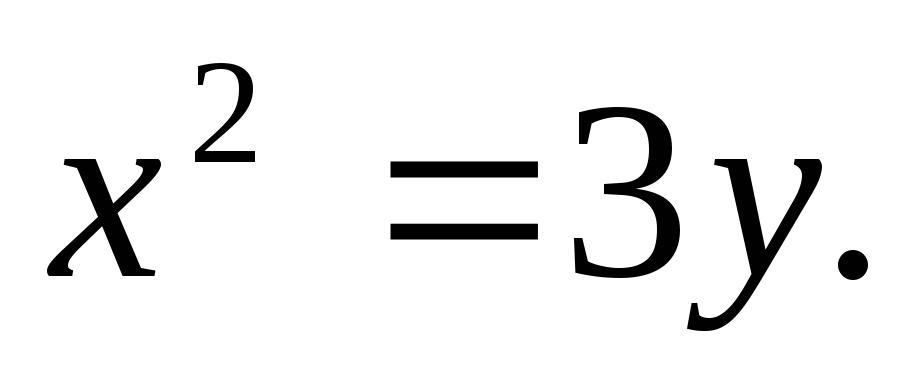
а)![]() б)
б)
![]() в)
в)
![]() г)
г)
![]()
-
Вычислить тройной интеграл:
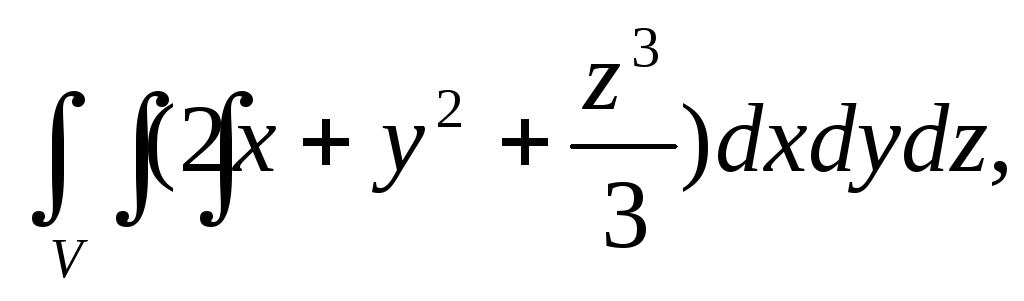 где область V
– прямоугольный параллелепипед (
где область V
– прямоугольный параллелепипед (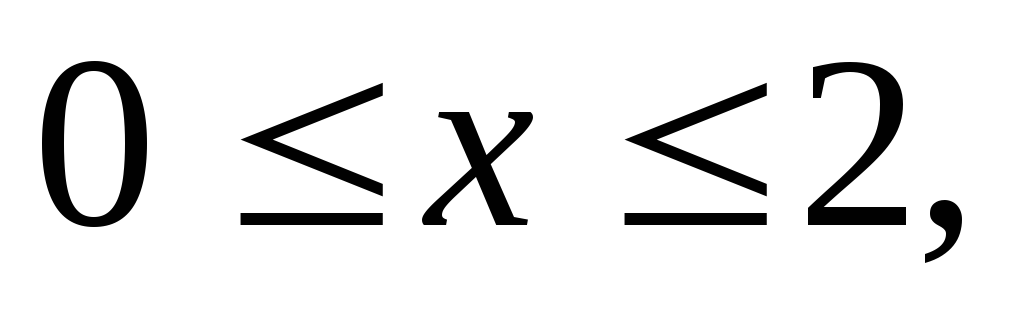
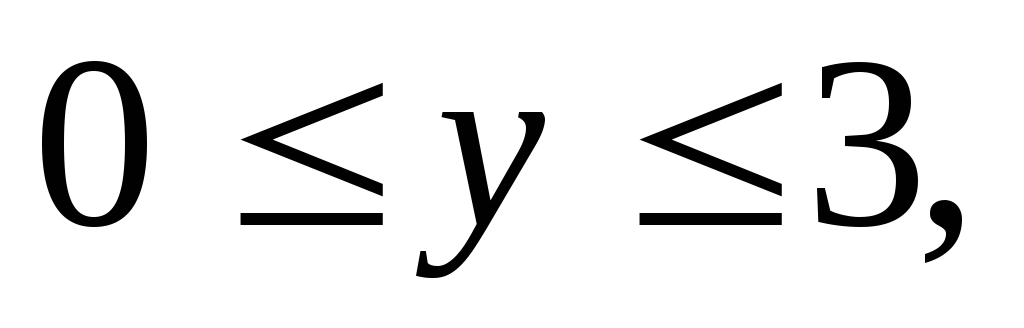
 ).
).
а)296, б)248, в)578, г)216.
-
Вычислить тройной интеграл:
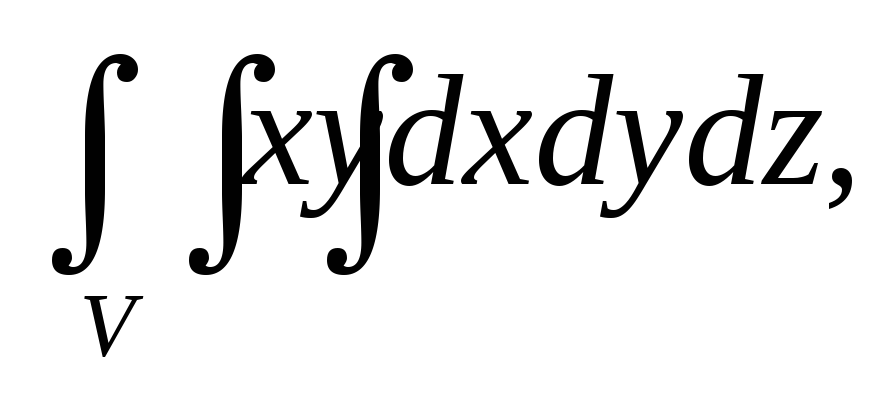 где область V
задается неравенствами
где область V
задается неравенствами



а) 10,5, б)7, в)3,5, г)5,25.
Вариант 3
-
Вычислить двойной интеграл:
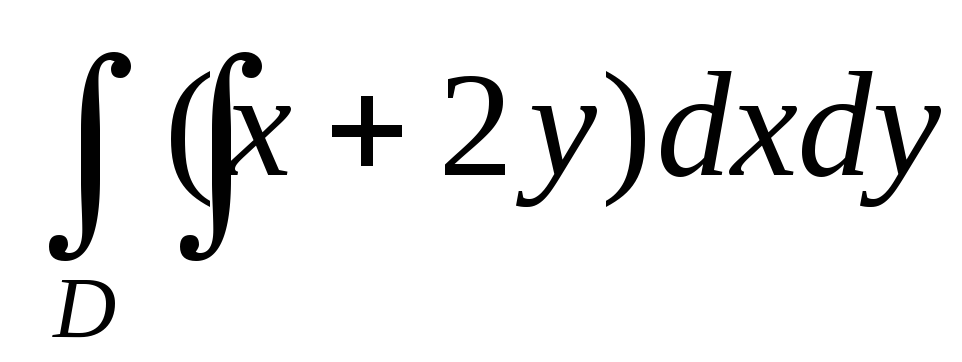 ,
,

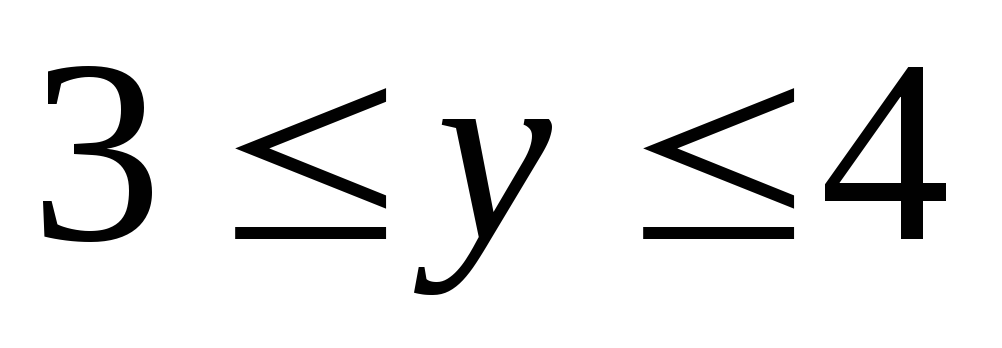 .
.
а)![]() б)
б)
![]() в)
в)
![]() г)0.
г)0.
-
Вычислить двойной интеграл:

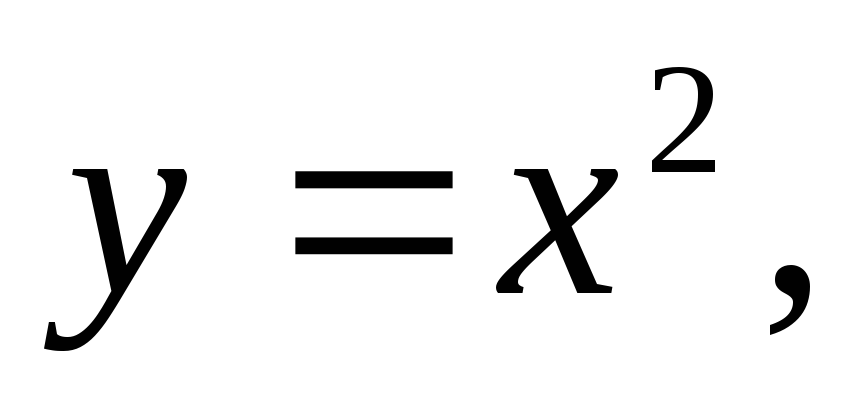

а)![]() б)
б)
![]() в)
в)
![]() г)
г)
![]()
-
Вычислить двойной интеграл, переходя к полярным координатам:
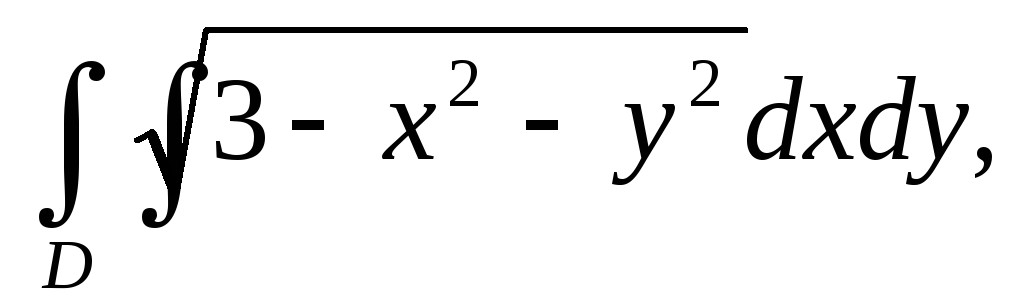

а)
![]() б)
б)
![]() в)
в)
![]() г)
г)
![]()
-
Найти площадь, ограниченную кривыми:
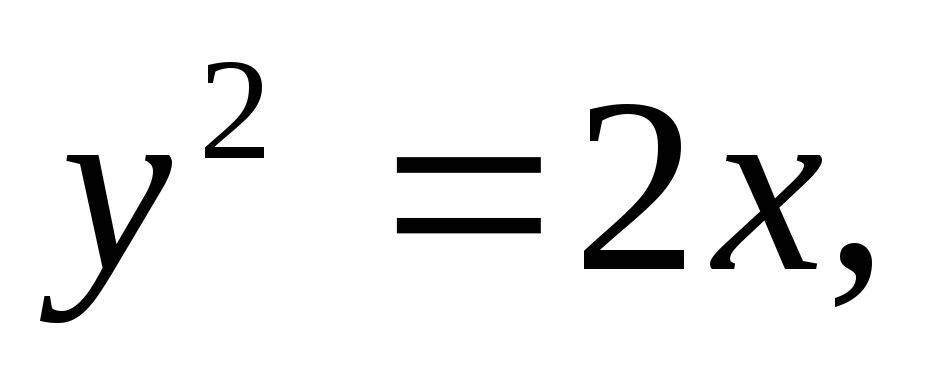
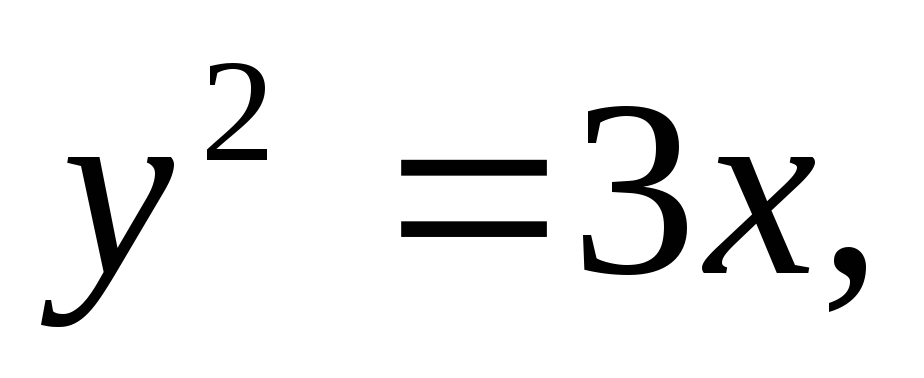


а)![]() б)
б)
![]() в)
в)
![]() г)
г)
![]()
-
Вычислить тройной интеграл:
 где область V
– прямоугольный параллелепипед (
где область V
– прямоугольный параллелепипед (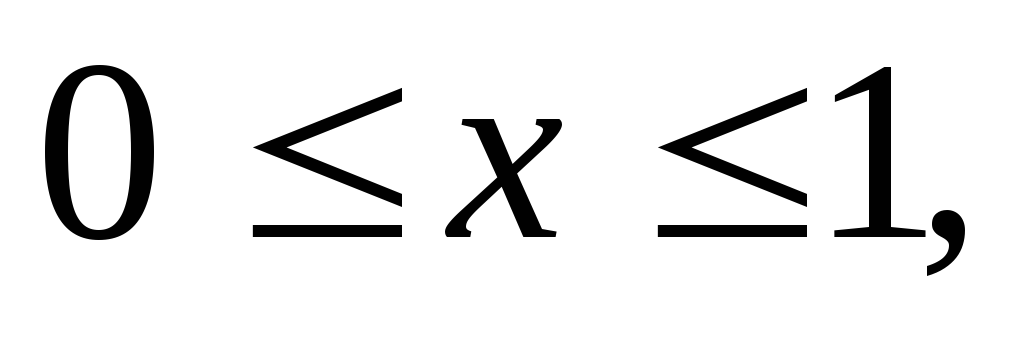

 ).
).
а)6, б)7,5, в)4, г)![]()
-
Вычислить тройной интеграл:
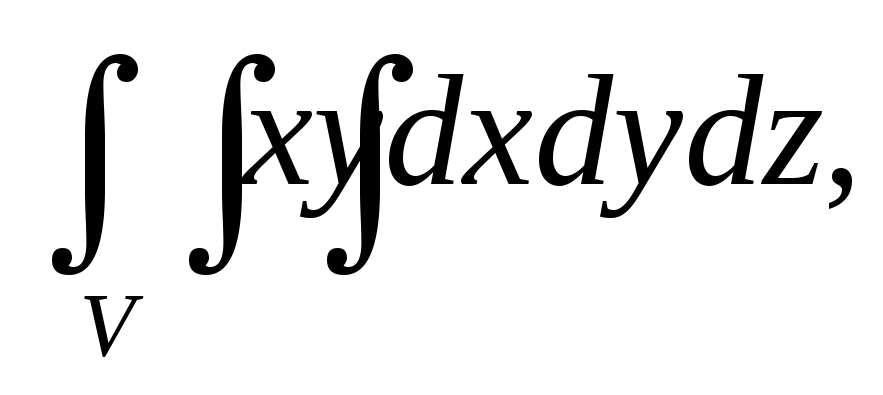 где область V
задается неравенствами
где область V
задается неравенствами
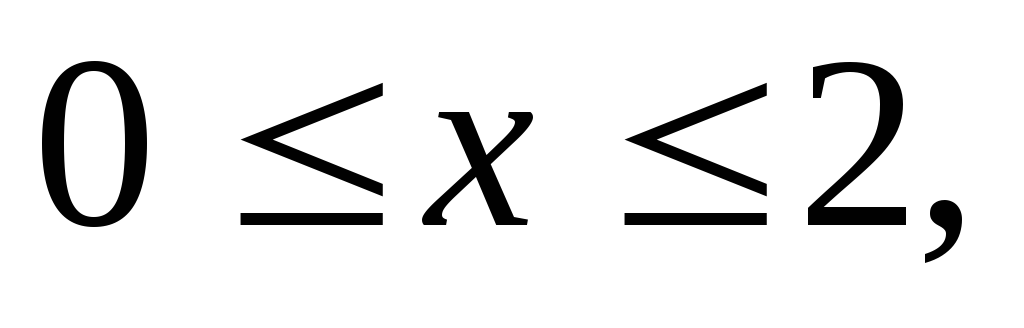

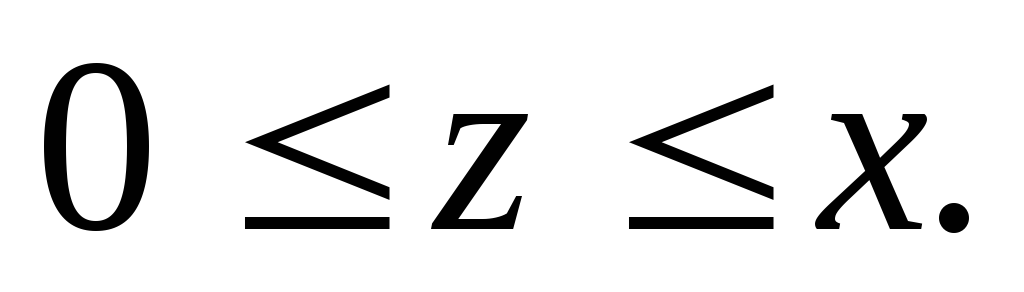
а)
![]() , б)28, в)
, б)28, в)![]() , г)14.
, г)14.
Вариант 4
-
Вычислить двойной интеграл:
 ,
,
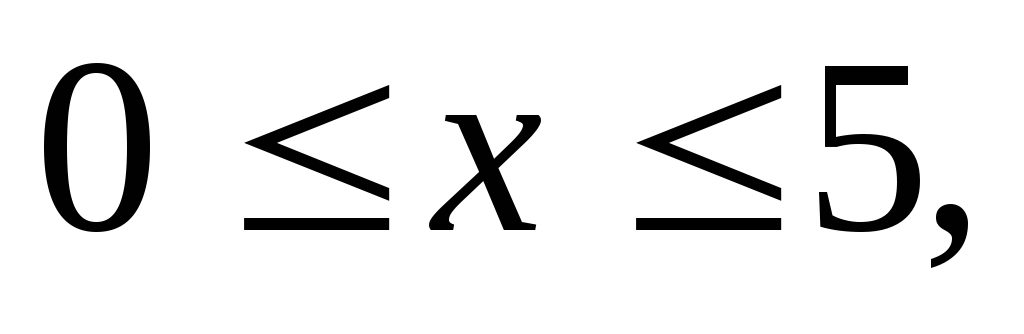
 .
.
а)0, б)20, в)![]() г)80.
г)80.
-
Вычислить двойной интеграл:
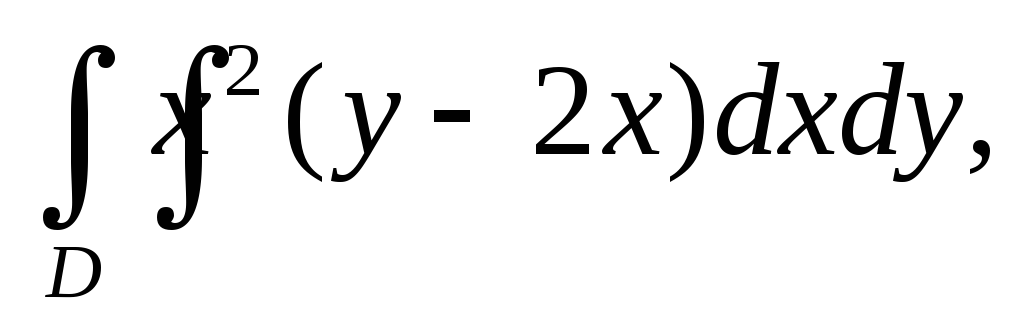
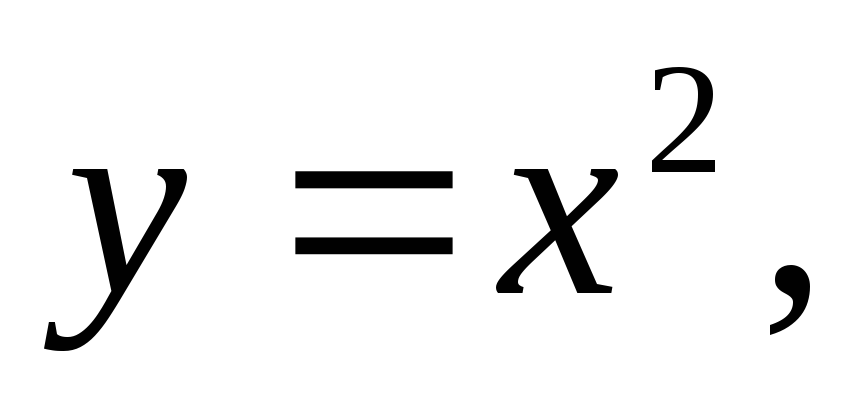

а)![]() б)
б)
![]() в)
в)
![]() г)
г)
![]()
-
Вычислить двойной интеграл, переходя к полярным координатам:
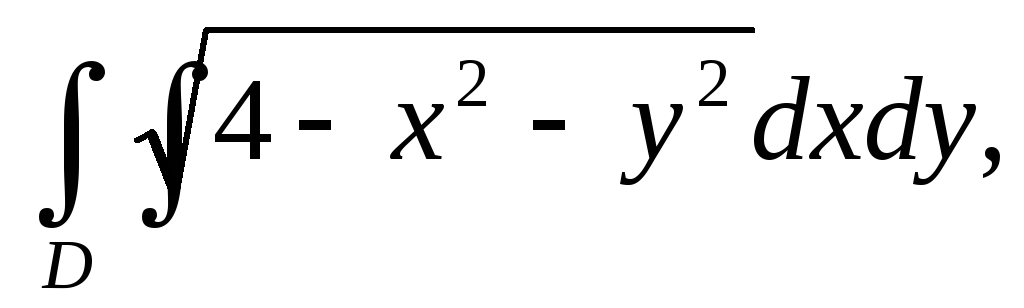
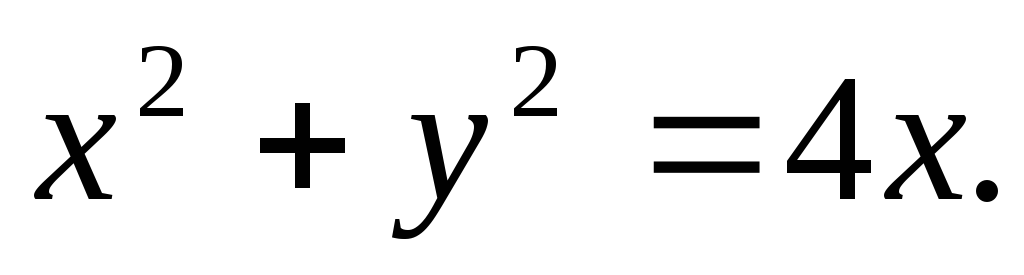
а)
![]() б)
б)
![]() в)
в)
![]() г)
г)
![]()
-
Найти площадь, ограниченную кривыми:
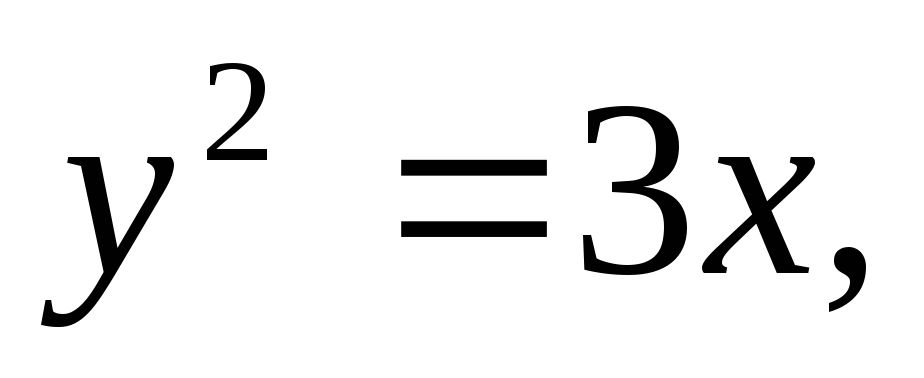

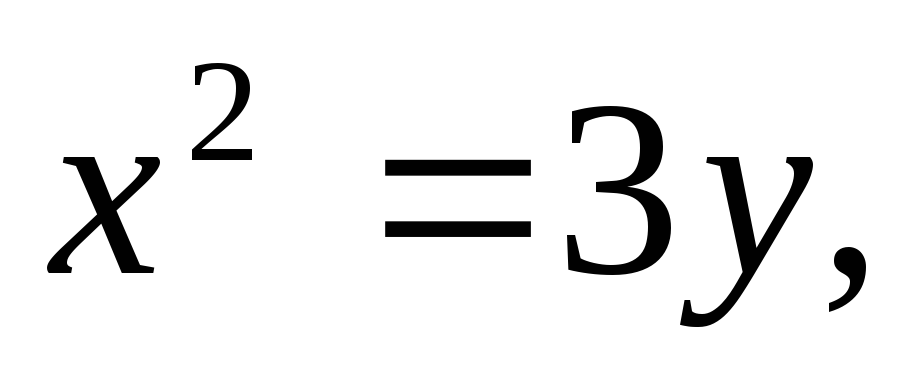

а)![]() б)
б)
![]() в)
в)
![]() г)
г)
![]()
-
Вычислить тройной интеграл:
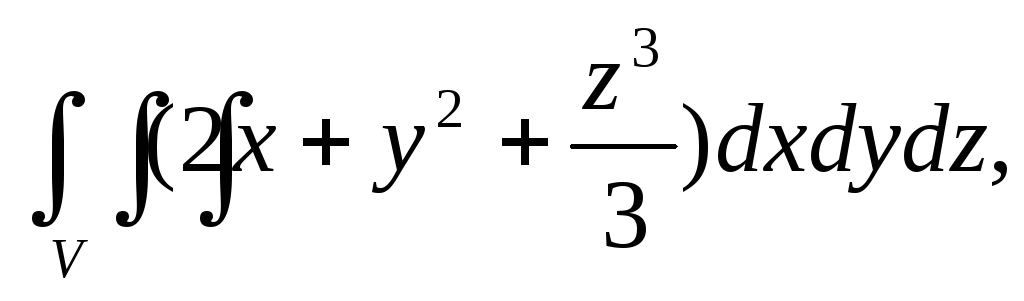 где область V
– прямоугольный параллелепипед (
где область V
– прямоугольный параллелепипед (
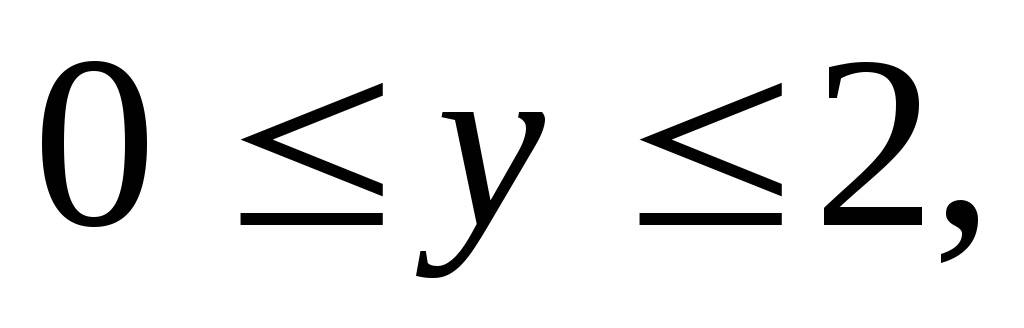
 ).
).
а)![]() , б)
, б)![]() , в)
, в)![]() , г)
, г)![]() .
.
-
Вычислить тройной интеграл:
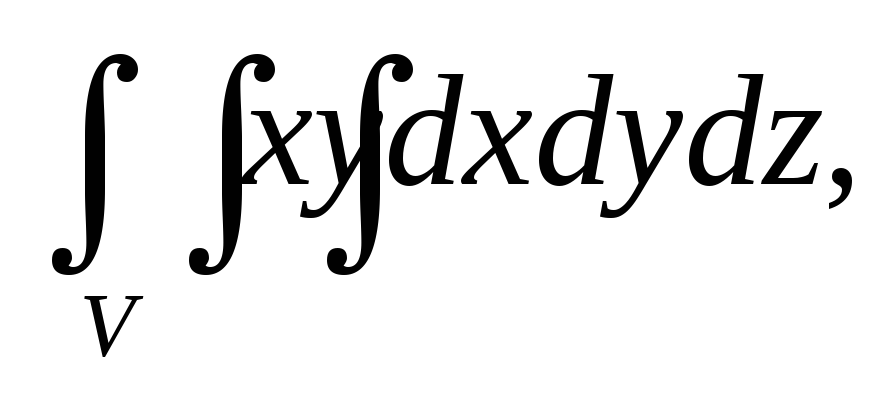 где область V
задается неравенствами
где область V
задается неравенствами
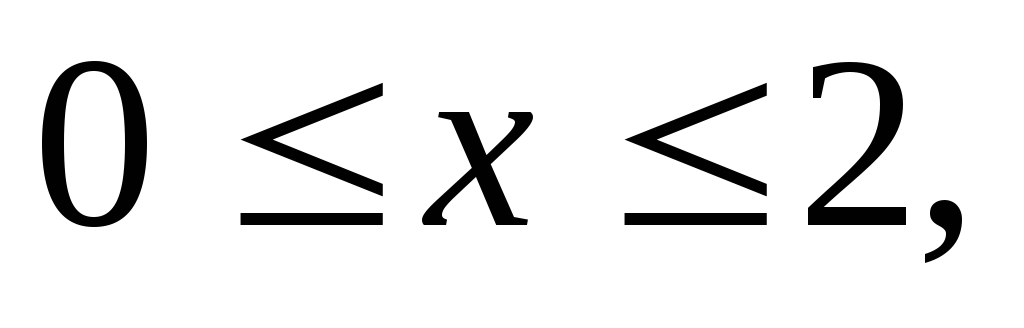
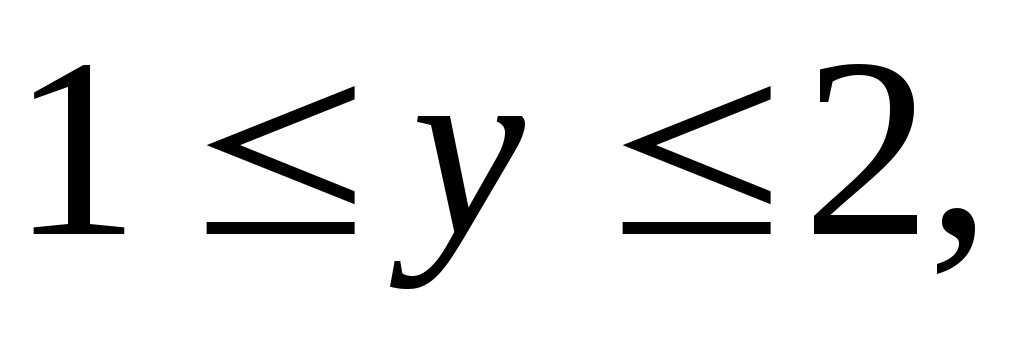

а) 12, б)8, в)6, г)4.
Вариант 5
-
Вычислить двойной интеграл:
 ,
,

 .
.
а)![]() б)
б)
![]() в)0, г)
в)0, г)
![]()
-
Вычислить двойной интеграл:


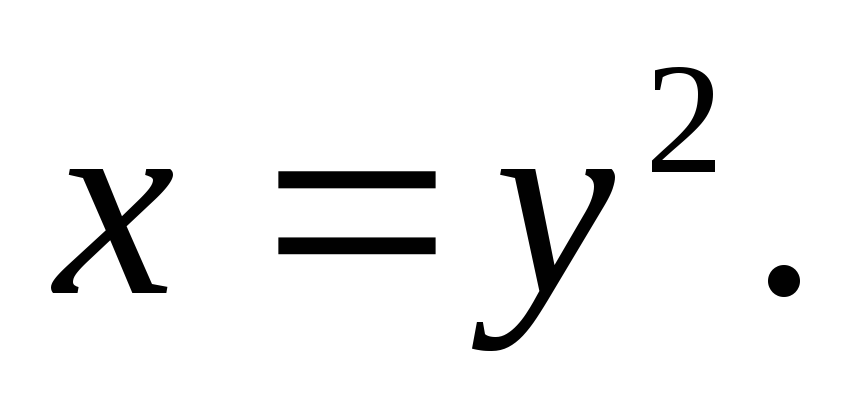
а)![]() б)
б)
![]() в)
в)
![]() г)
г)
![]()
-
Вычислить двойной интеграл, переходя к полярным координатам:
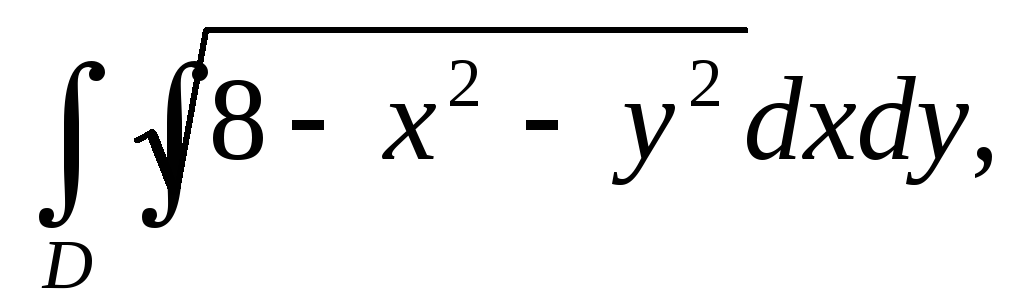
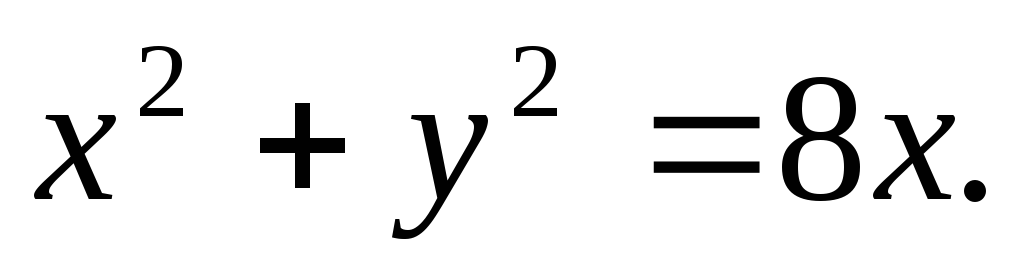
а)
![]() б)
б)
![]() в)
в)
![]() г)
г)
![]()
-
Найти площадь, ограниченную кривыми:



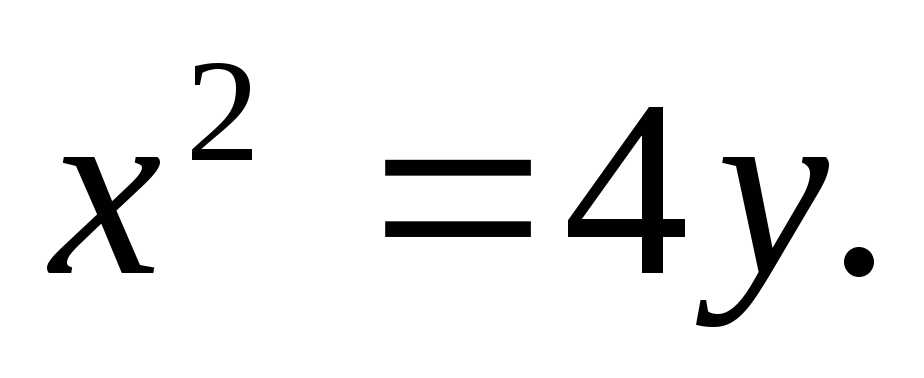
а)![]() б)
б)
![]() в)
в)
![]() г)
г)
![]()
-
Вычислить тройной интеграл:
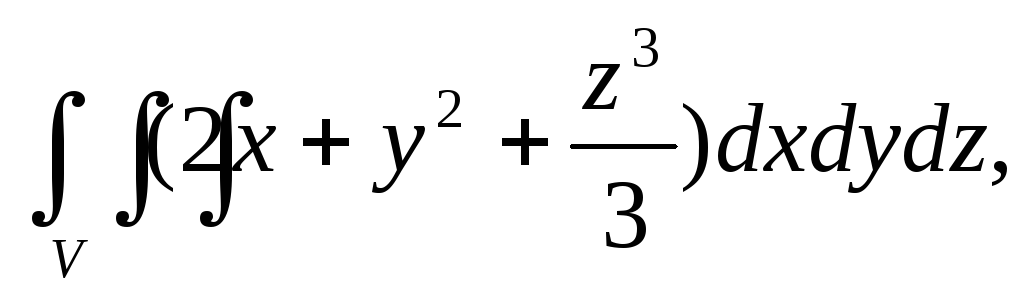 где область V
– прямоугольный параллелепипед (
где область V
– прямоугольный параллелепипед (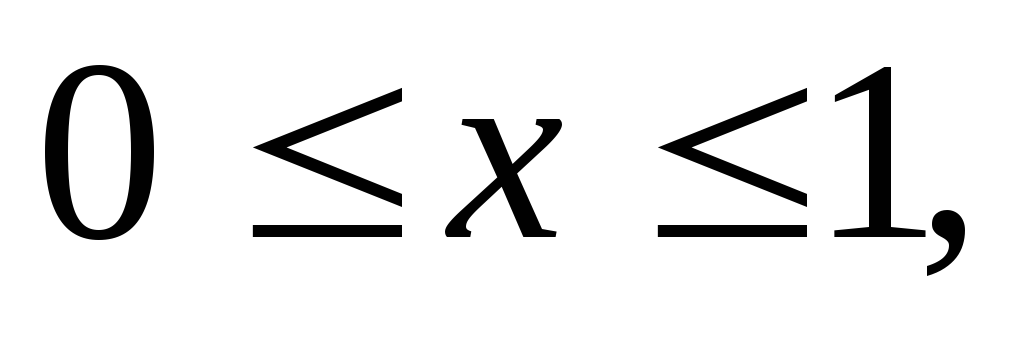
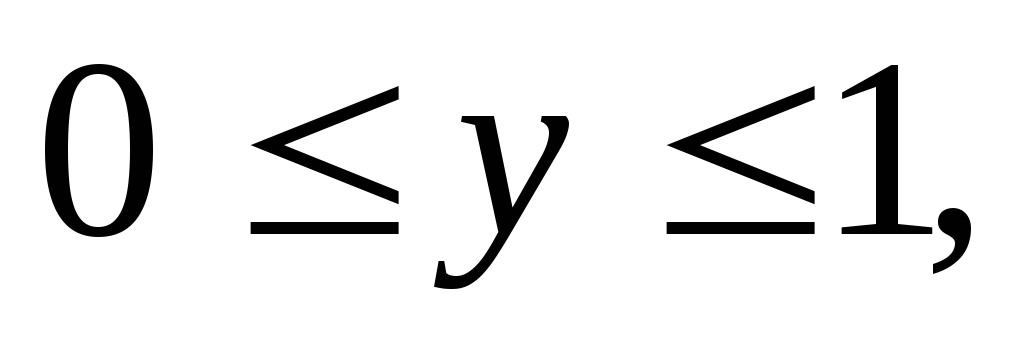
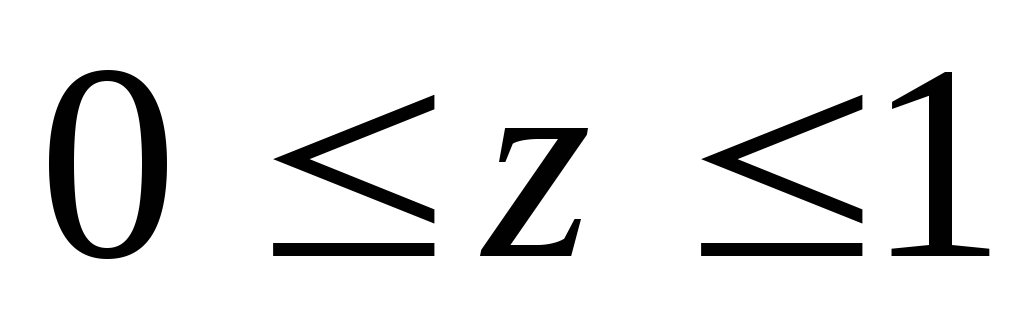 ).
).
а)![]() , б)
, б)![]() , в)
, в)![]() , г)
, г)![]() .
.
-
Вычислить тройной интеграл:
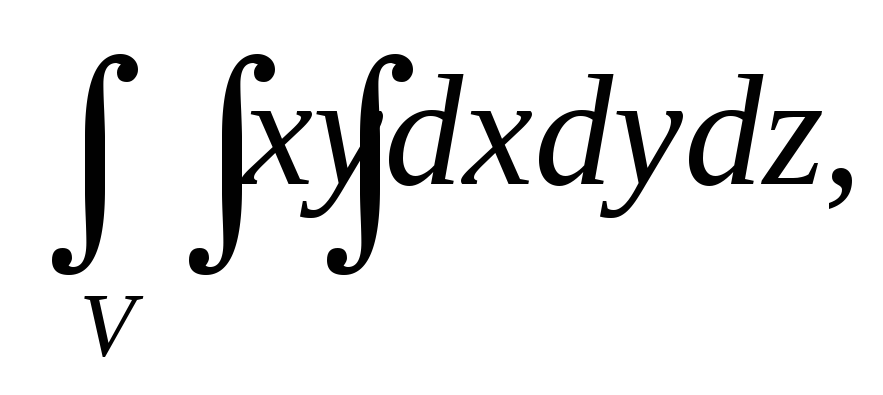 где область V
задается неравенствами
где область V
задается неравенствами
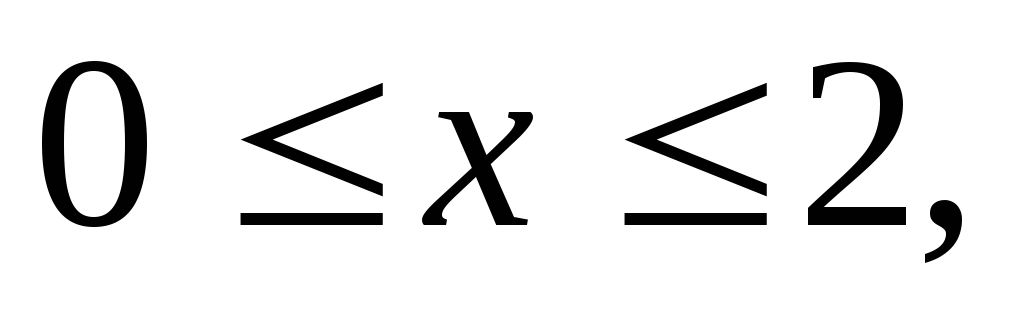
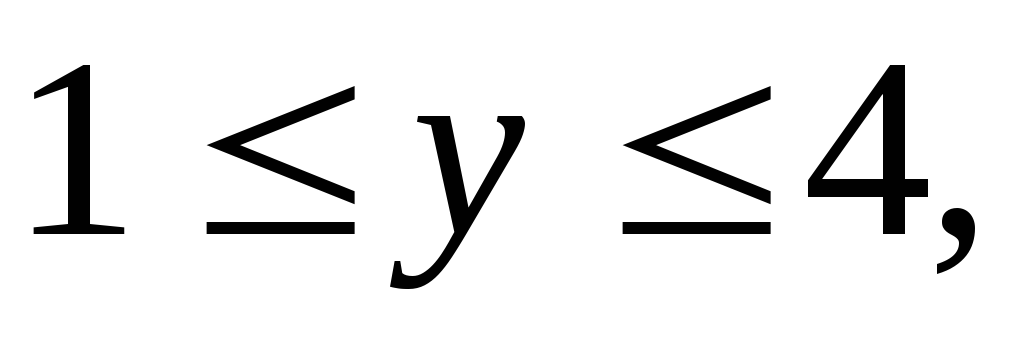

а)
![]() , б)
, б)![]() , в)35, г)
, в)35, г)![]() .
.
Вариант 6
-
Вычислить двойной интеграл:
 ,
,
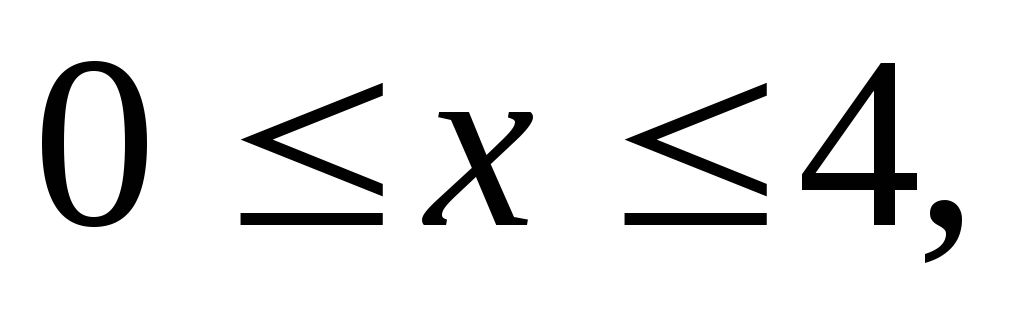
 .
.
а)56, б)176, в)0, г)32.
-
Вычислить двойной интеграл:

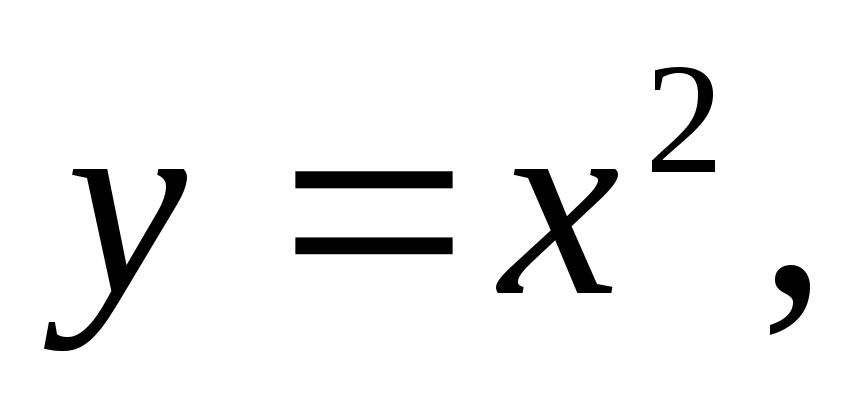
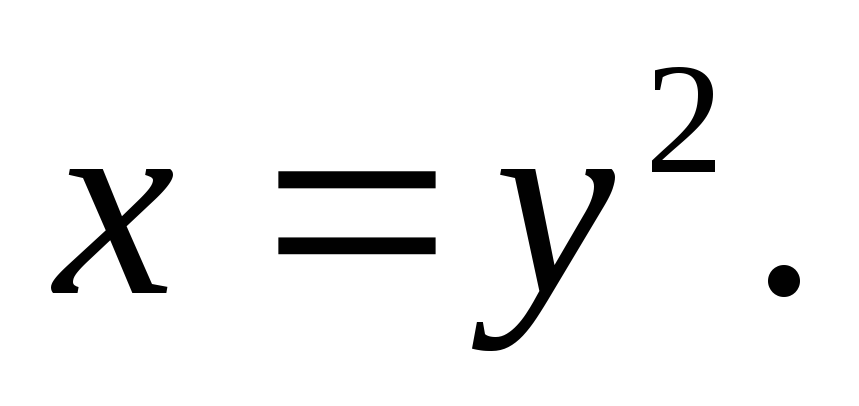
а)![]() б)
б)
![]() в)
в)
![]() г)
г)
![]()
-
Вычислить двойной интеграл, переходя к полярным координатам:
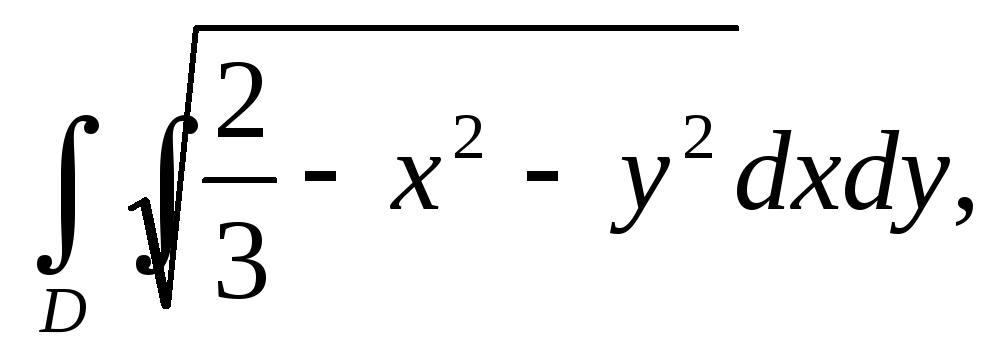
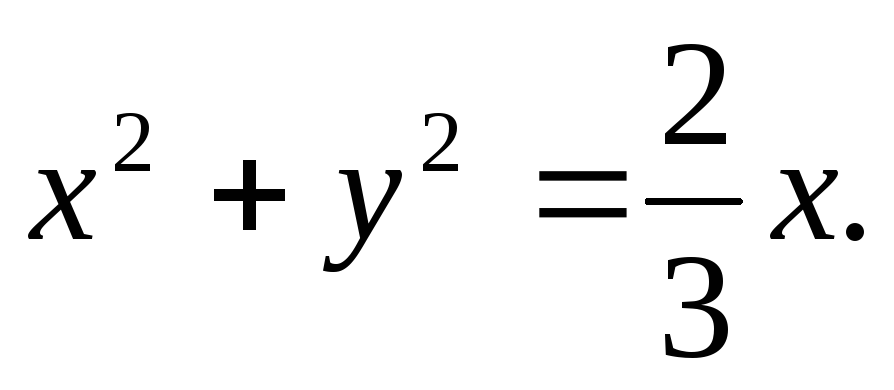
а)
![]() б)
б)
![]() в)
в)
![]() г)
г)
![]()
-
Найти площадь, ограниченную кривыми:
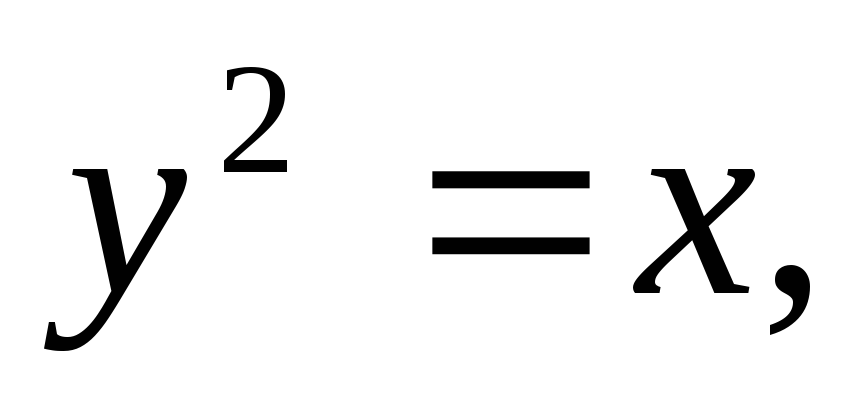
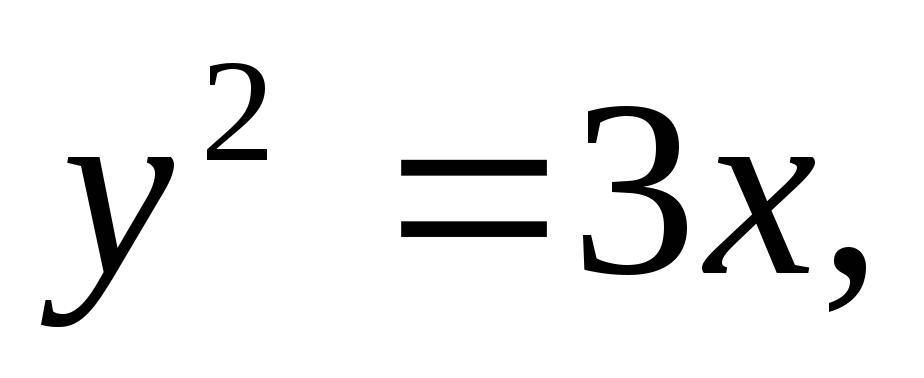

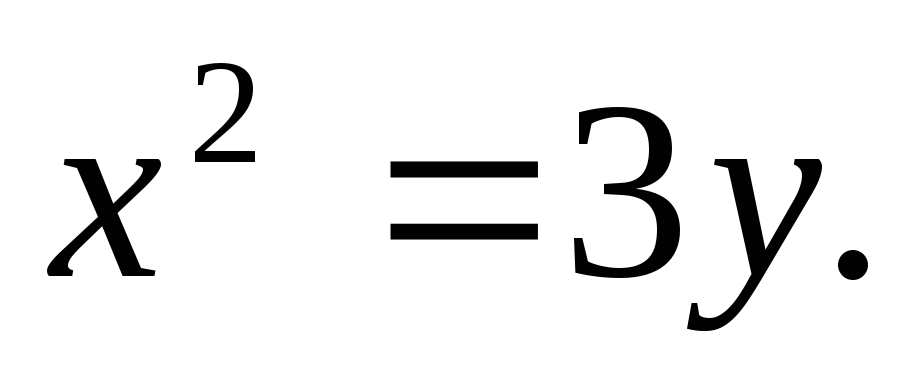
а)![]() б)
б)
![]() в)
в)
![]() г)
г)
![]()
-
Вычислить тройной интеграл:
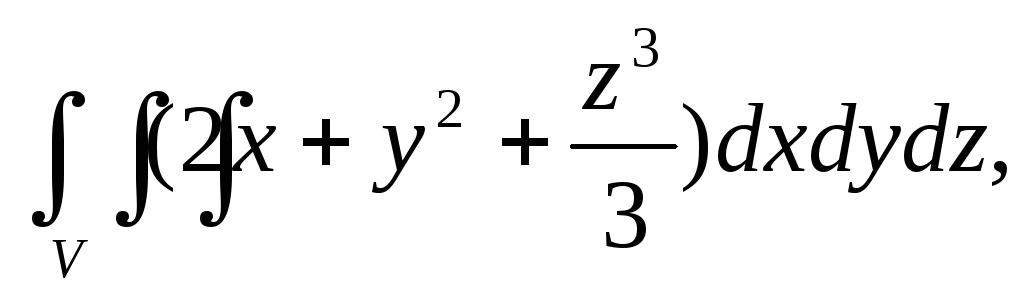 где область V
– прямоугольный параллелепипед (
где область V
– прямоугольный параллелепипед (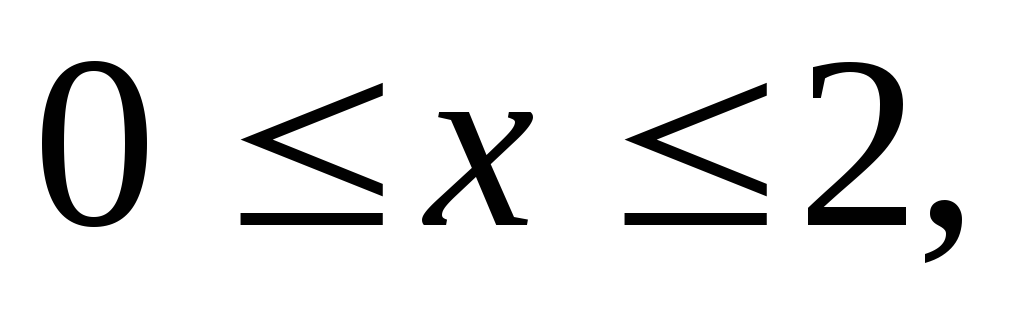
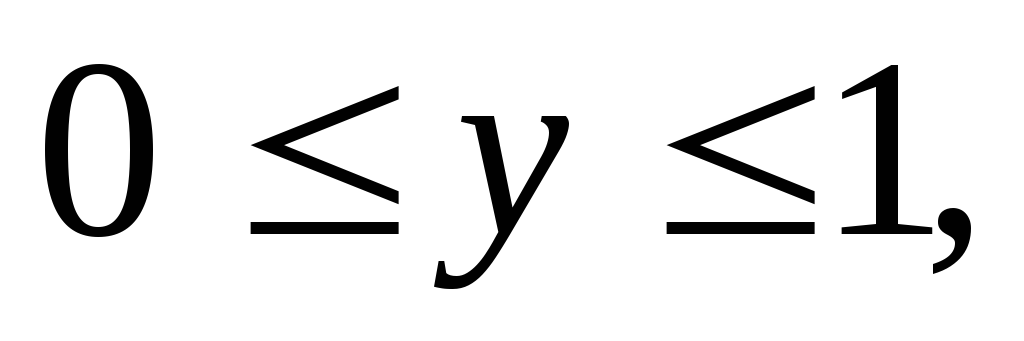
 ).
).
а)![]() , б)
, б)![]() , в)
, в)![]() , г)
, г)![]() .
.
-
Вычислить тройной интеграл:
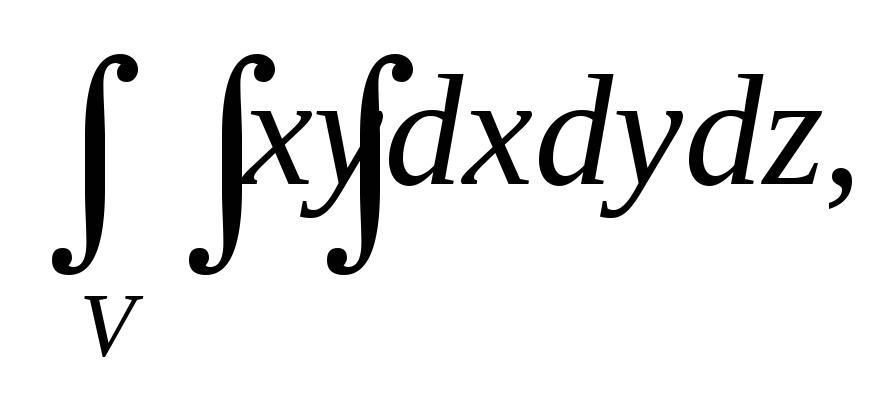 где область V
задается неравенствами
где область V
задается неравенствами

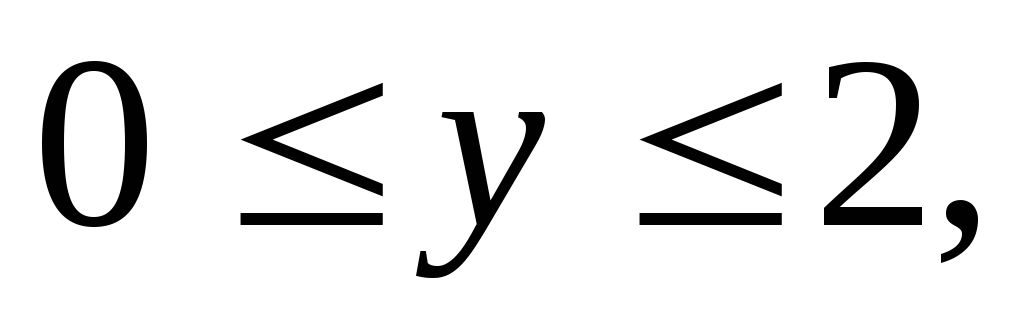
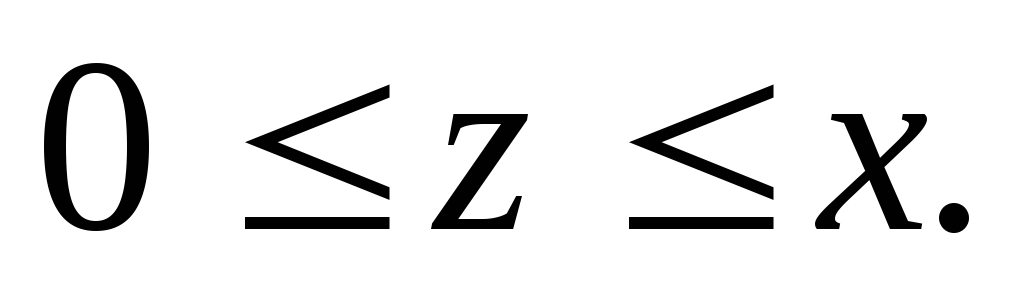
а)
![]() , б)14, в)
, б)14, в)![]() , г)7.
, г)7.
Вариант 7
-
Вычислить двойной интеграл:
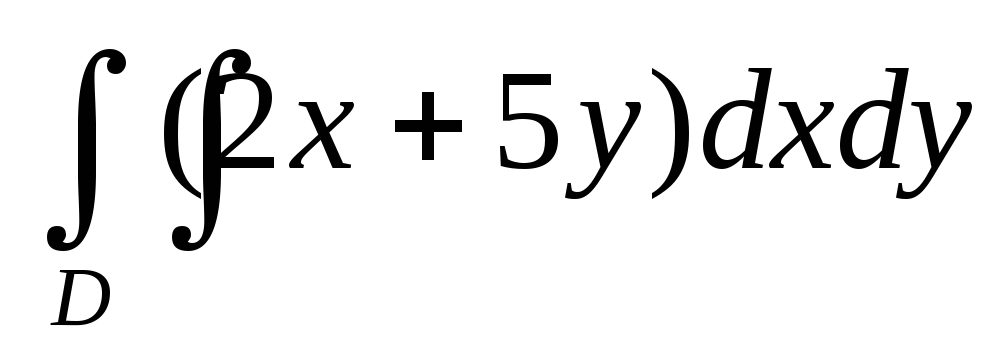 ,
,
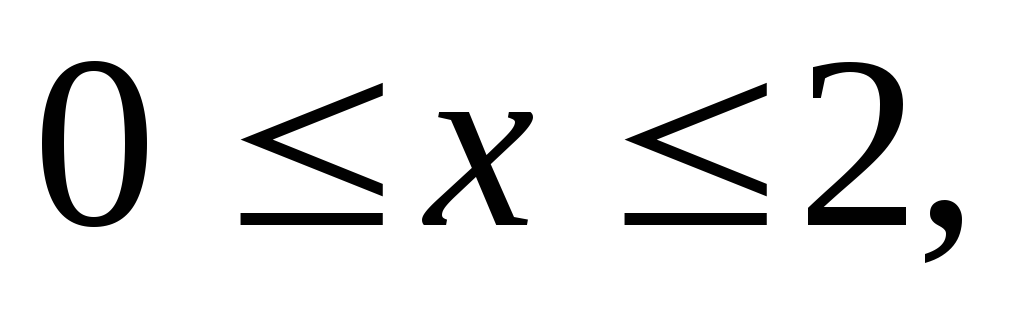
 .
.
а)9, б)0, в)29, г)0.
-
Вычислить двойной интеграл:


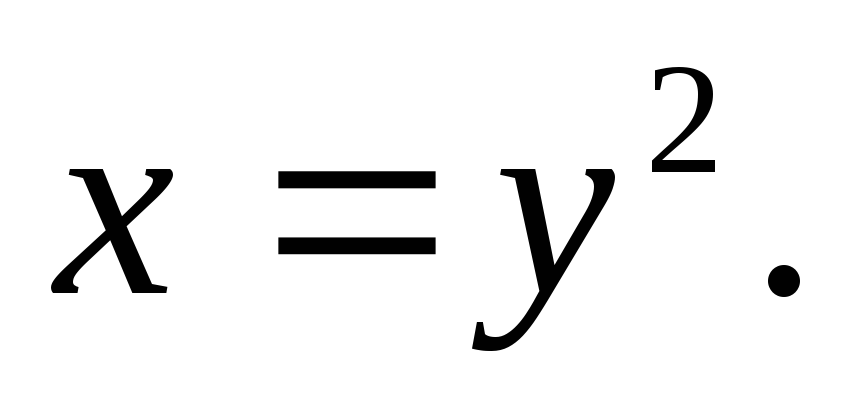
а)![]() б)
б)
![]() в)
в)
![]() г)
г)
![]()
-
Вычислить двойной интеграл, переходя к полярным координатам:

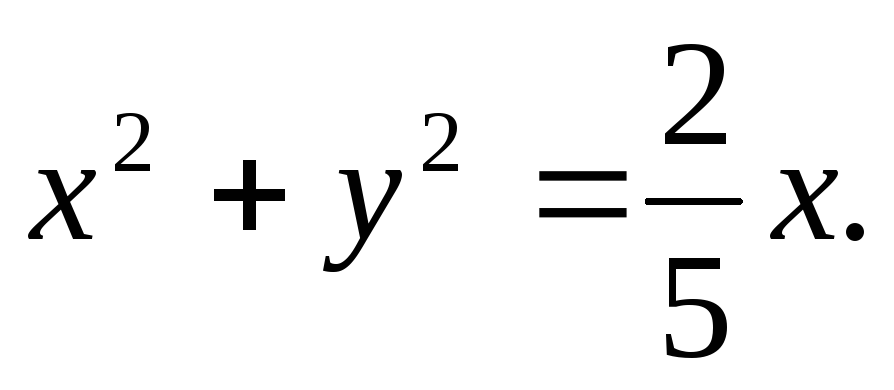
а)
![]() б)
б)
![]() в)
в)
![]() г)
г)
![]()
-
Найти площадь, ограниченную кривыми:
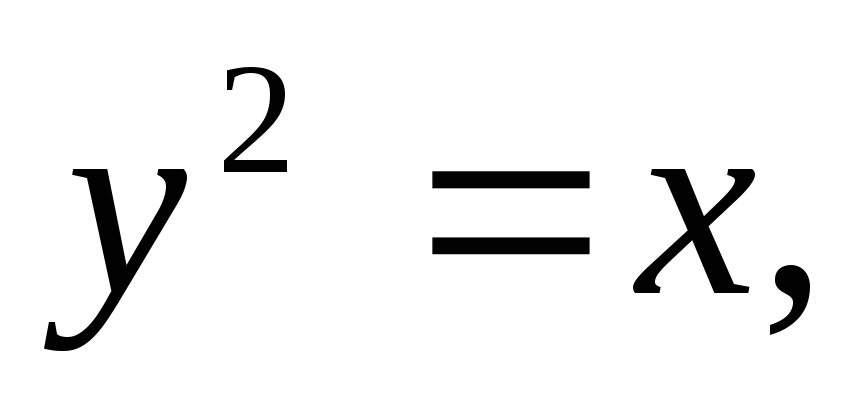


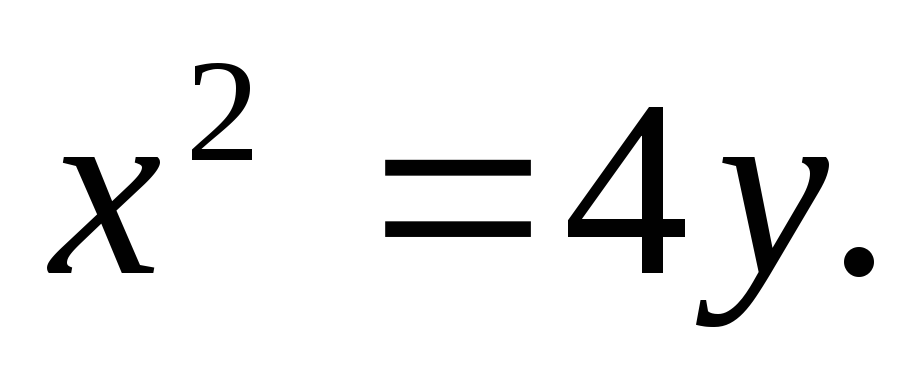
а)![]() б)
б)
![]() в)
в)
![]() г)
г)
![]()
-
Вычислить тройной интеграл:
 где область V
– прямоугольный параллелепипед (
где область V
– прямоугольный параллелепипед (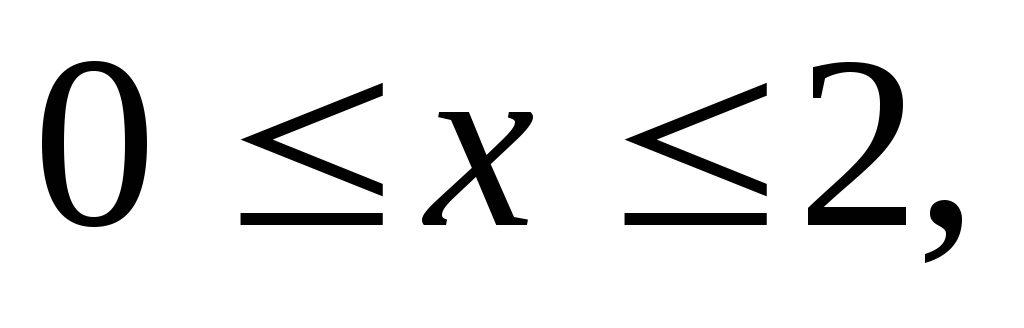
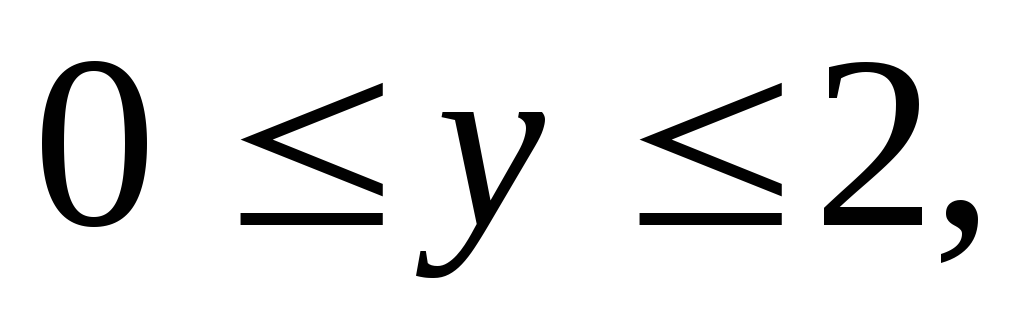
 ).
).
а)![]() , б)
, б)![]() , в)
, в)![]() , г)19.
, г)19.
-
Вычислить тройной интеграл:
 где область V
задается неравенствами
где область V
задается неравенствами

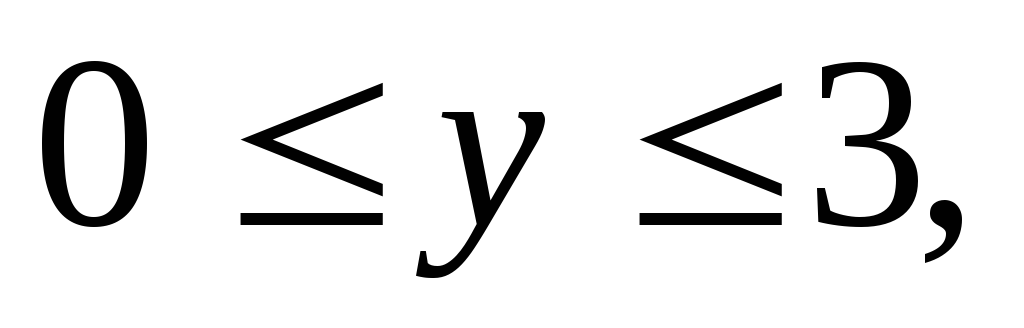
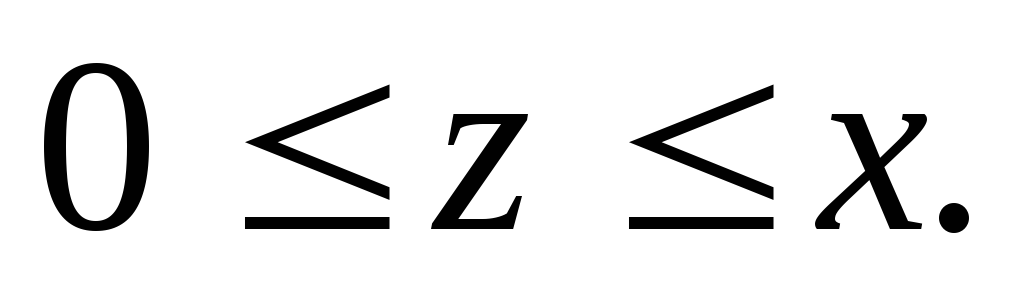
а)
![]() , б)21, в)
, б)21, в)![]() , г)
, г)![]() .
.
Вариант 8
-
Вычислить двойной интеграл:
 ,
,

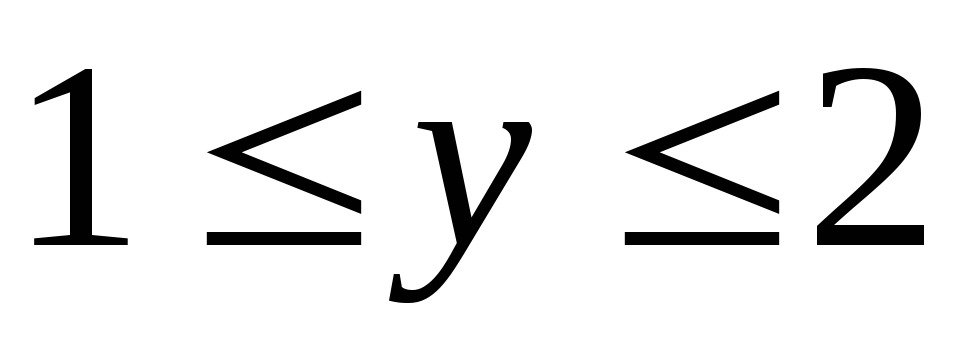 .
.
а)0, б)11, в)3, г)25.
-
Вычислить двойной интеграл:


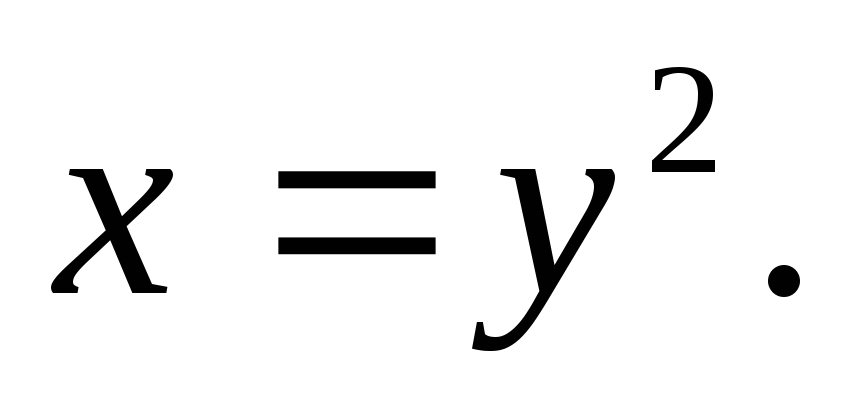
а)![]() б)
б)
![]() в)
в)
![]() г)
г)
![]()
-
Вычислить двойной интеграл, переходя к полярным координатам:


а)
![]() б)
б)
![]() в)
в)
![]() г)
г)
![]()
-
Найти площадь, ограниченную кривыми:
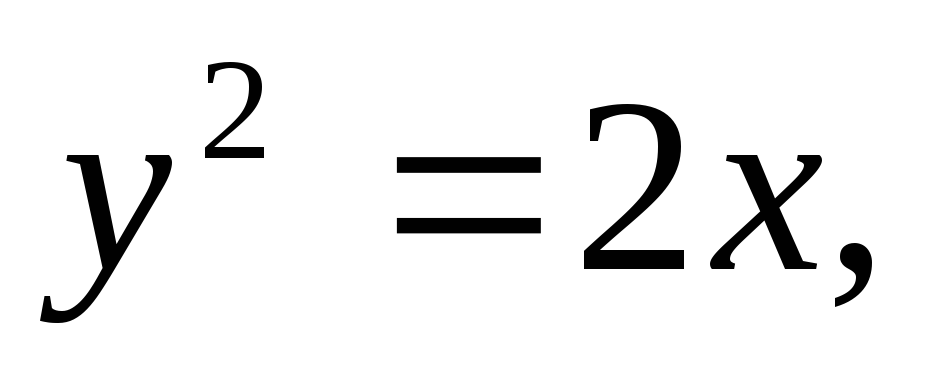
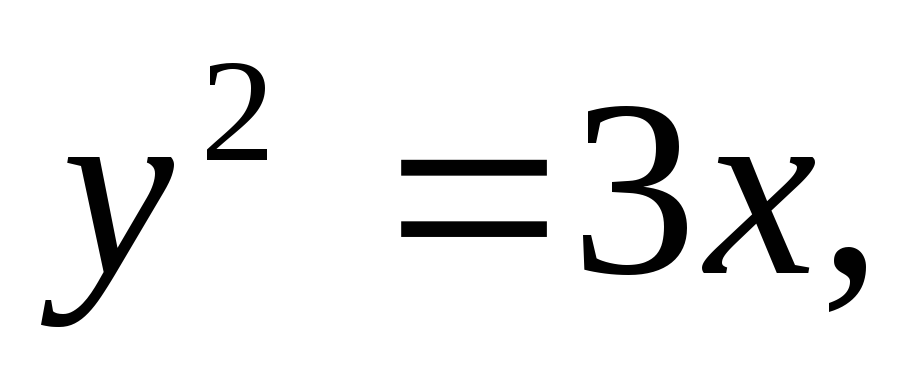
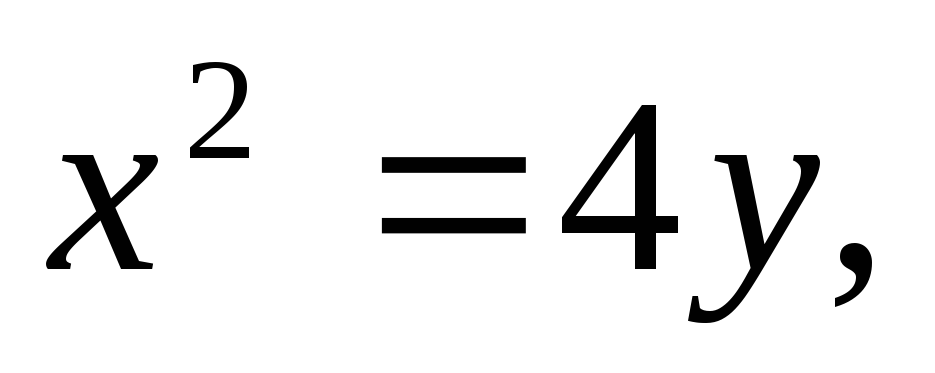

а)![]() б)
б)
![]() в)
в)
![]() г)
г)
![]()
-
Вычислить тройной интеграл:
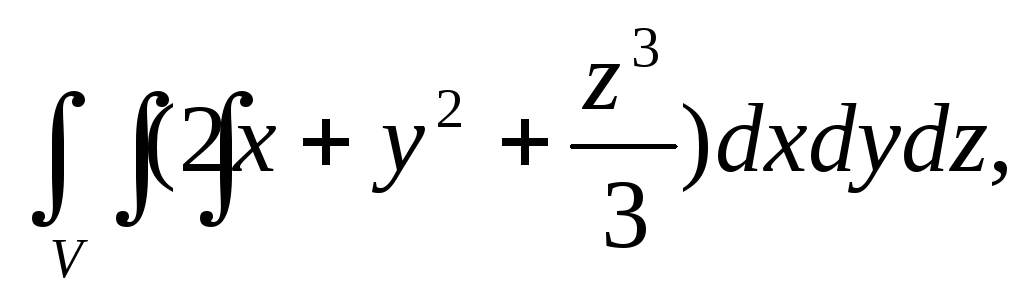 где область V
– прямоугольный параллелепипед (
где область V
– прямоугольный параллелепипед (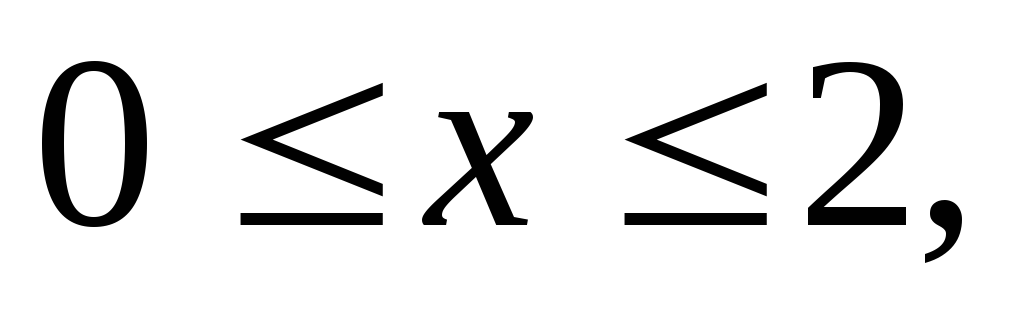
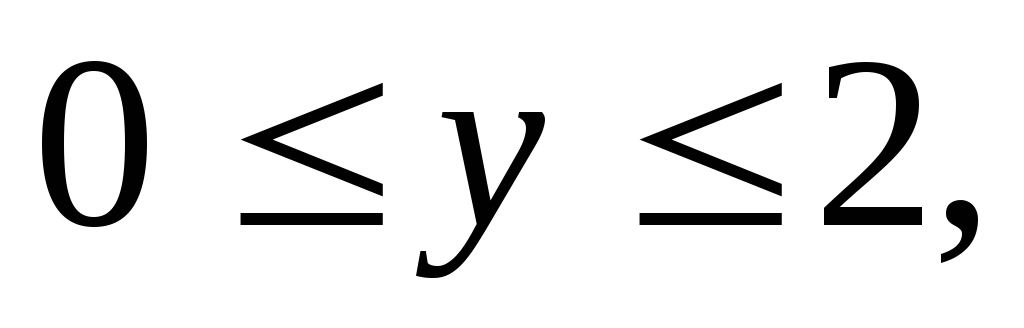
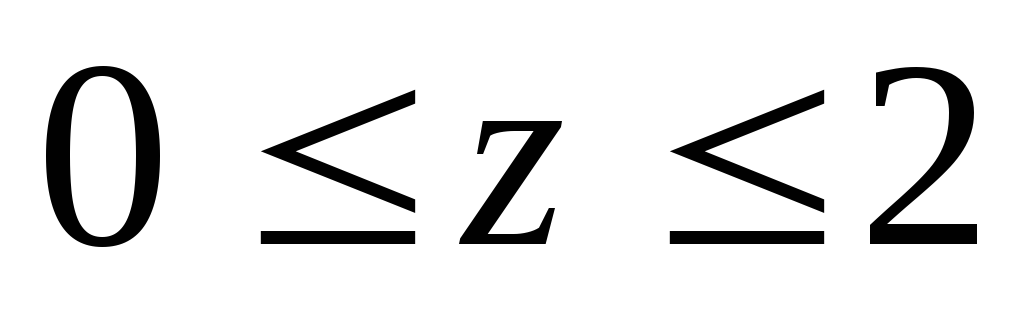 ).
).
а)48, б)24, в)32, г)40.
-
Вычислить тройной интеграл:
 где область V
задается неравенствами
где область V
задается неравенствами
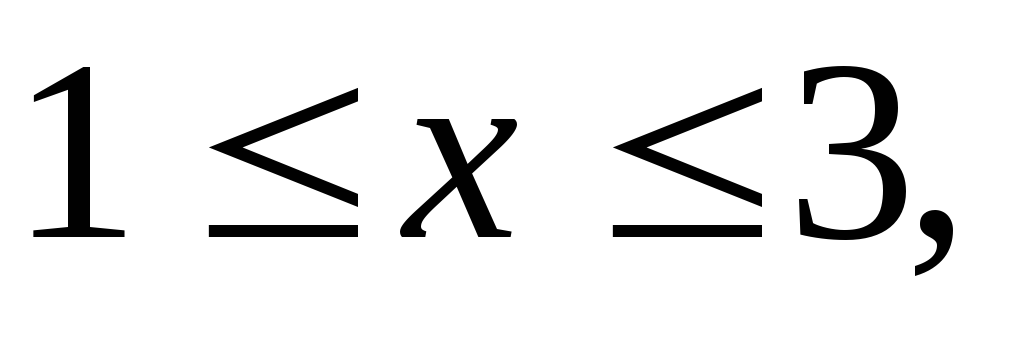


а) 117, б)78, в)58,5, г)39.
Вариант 9
-
Вычислить двойной интеграл:
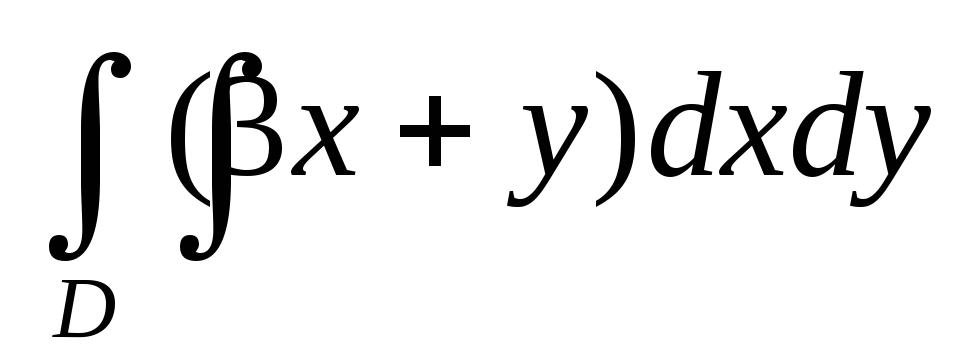 ,
,
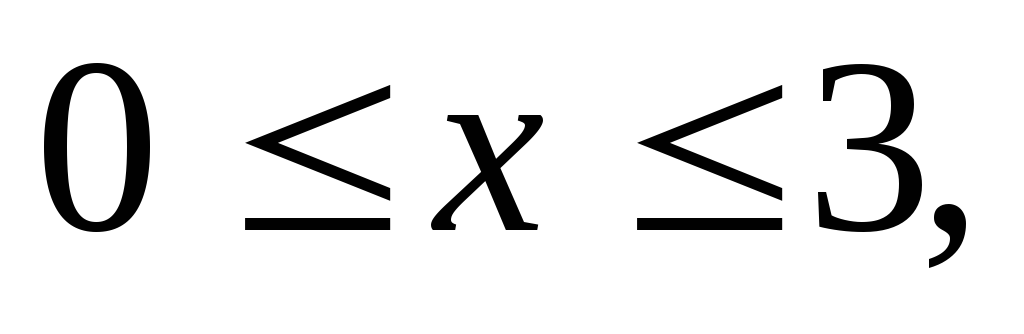
 .
.
а)39, б)12, в)0, г)33.
-
Вычислить двойной интеграл:
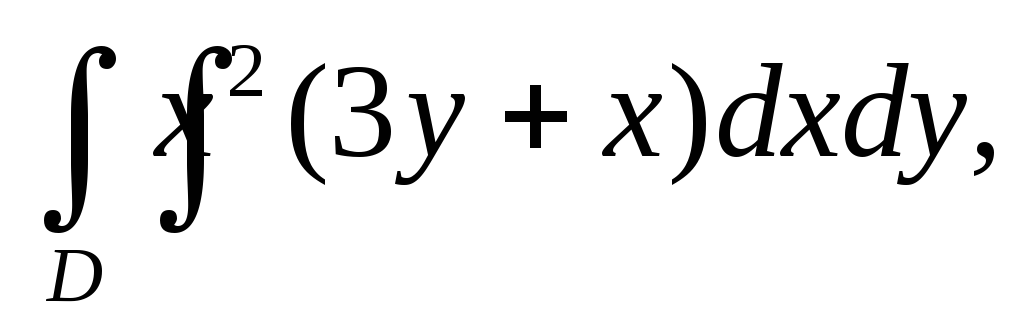


а)![]() б)
б)
![]() в)
в)
![]() г)
г)
![]()
-
Вычислить двойной интеграл, переходя к полярным координатам:
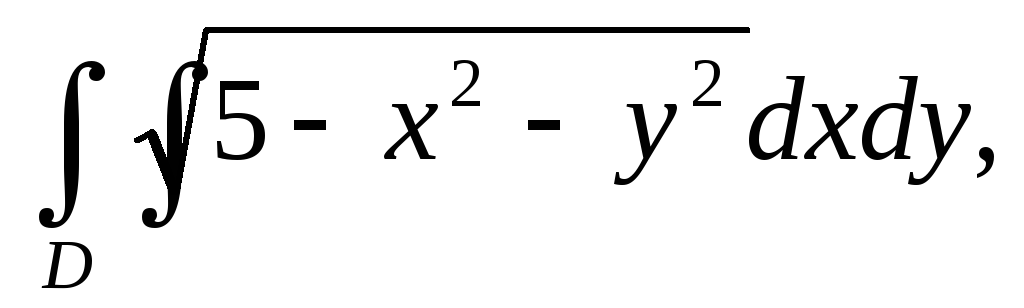
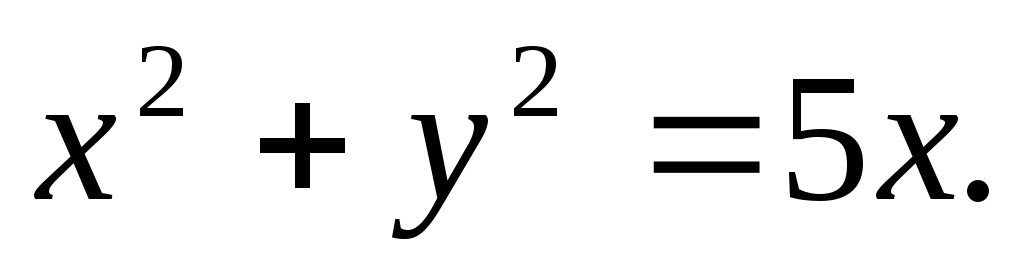
а)
![]() б)
б)
![]() в)
в)
![]() г)
г)
![]()
-
Найти площадь, ограниченную кривыми:
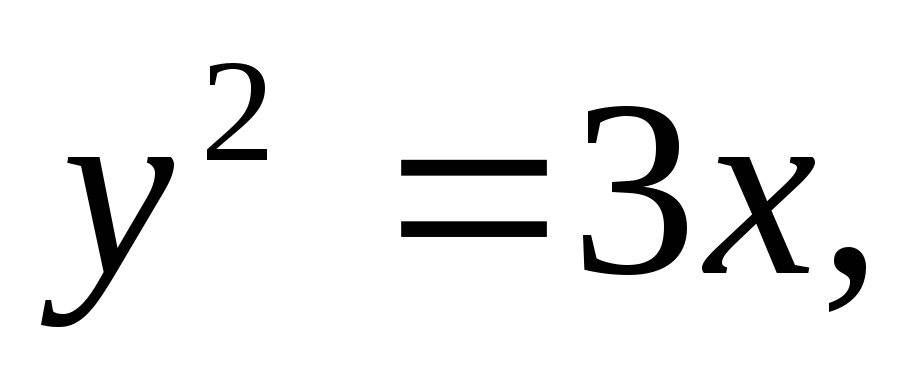
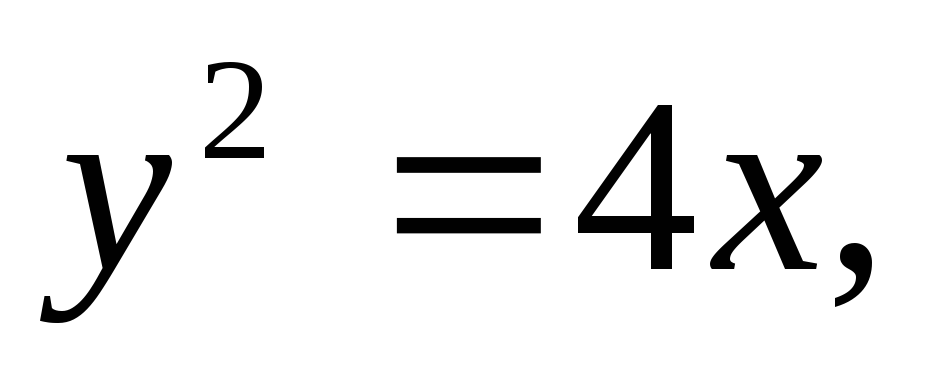
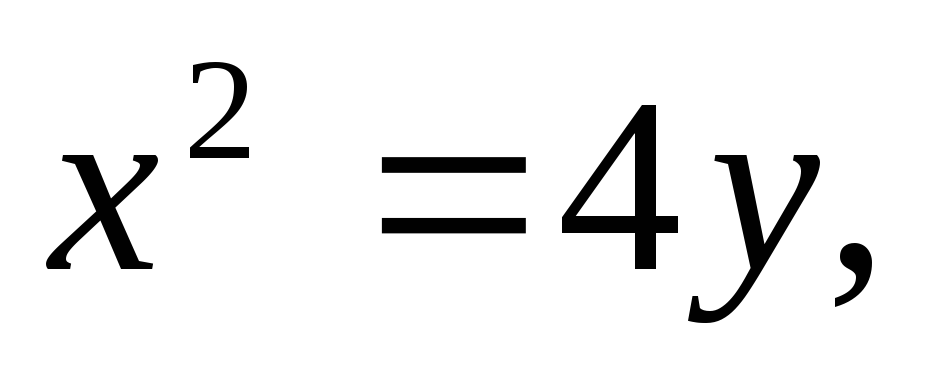
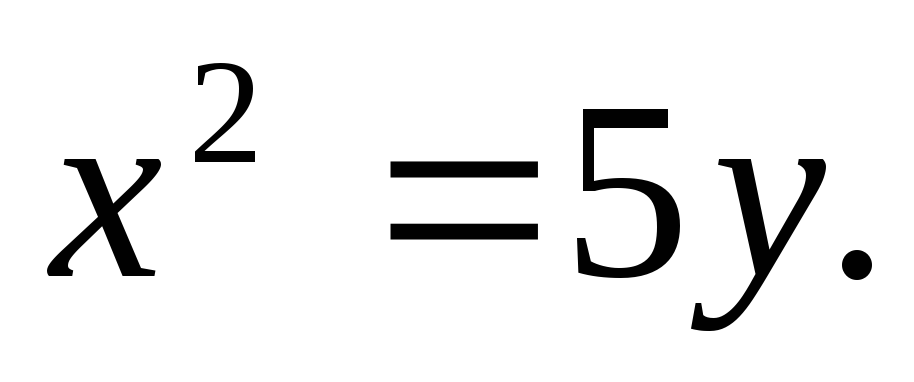
а)![]() б)
б)
![]() в)
в)
![]() г)
г)
![]()
-
Вычислить тройной интеграл:
 где область V
– прямоугольный параллелепипед (
где область V
– прямоугольный параллелепипед (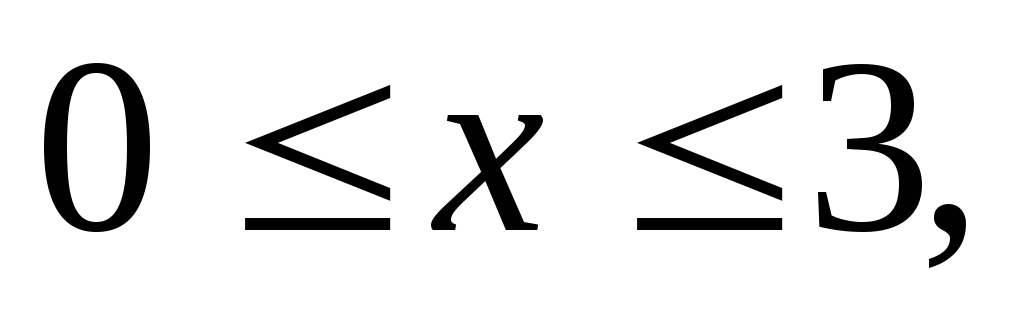

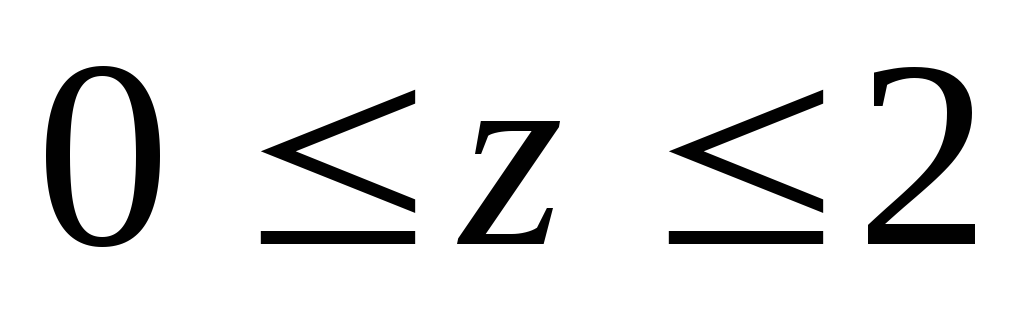 ).
).
