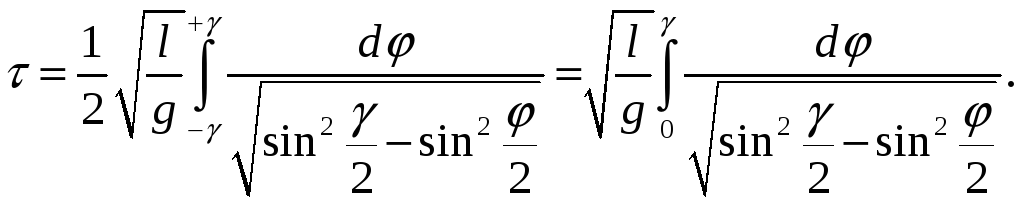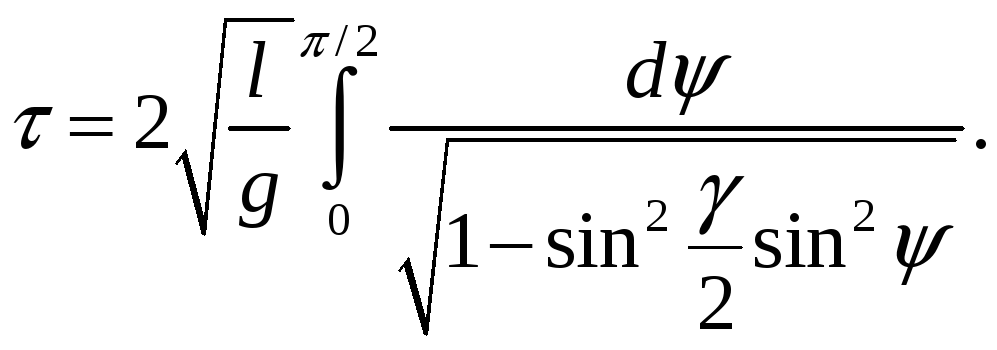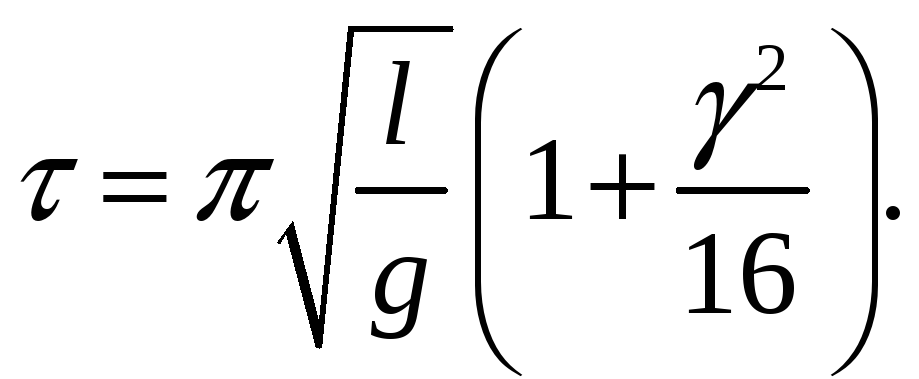Физпрактикум (labs) / Маглаб 3

Лабораторная работа №3.

КРУГОВОЙ МАЯТНИК

Цель работы: выяснение зависимости периода колебаний физического маятника от угла отклонения и сравнение полученных данных с расчетными.

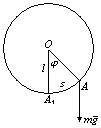
Круговой математический маятник

Рисунок 1

Материальная точка, принужденная двигаться в вертикальной плоскости по заданной динамически гладкой окружности (рис.1) при действии силы тяжести, называется круговым математическим маятником. Радиус l окружности называется длиной кругового маятника (рис.1). Чтобы практически реализовать систему, приближённую к круговому математическому маятнику, можно закрепить небольшой массивный груз на жёстком лёгком подвесе. Положение маятника определяется углом φ, составляемым его радиусом с нисходящей вертикалью, причем угол, отсчитанный в направлении против хода часовой стрелки, считается положительным, а отсчитанный по ходу часовой стрелки – отрицательным. Угол φ определяется из дифференциального уравнения.

(1)

при начальных данных Скорость при этом дается формулой

(2)

При маятник совершает полные обороты. При можно найти угол  такой, что

(3)

В этом случае

(4)

и движение маятника представляет колебание по дуге . Период размаха определяется формулой

(5)

Подстановка дает:

(6)

Полученный интеграл называется полным эллиптическим интегралом первого рода и обозначается

(7)

так что

(8)

Значение К зависит от  , так что колебания маятника не тавтохронны. Значения К можно брать из таблицы:

	К			К
0	1,5708		60	1,6258
5	1,5715		90	1,8541
10	1,5738		120	2,1565
20	1,5828		150	2,7681
40	1,6200		180	∞

Приближенная формула для К при небольших значениях  имеет вид:

(9)

При весьма малых  полагают и тогда

(10)

Если  столь мало, что членом можно пренебречь, то

(11)

Получили формулу периода колебаний маятника, известную ещё из курса физики средней школы. Так как эта формула не содержит  , то малые колебания маятника можно считать тавтохронными.

Круговой физический маятник

Рисунок 2

Физическим маятником называется тяжелое твердое тело, вращающееся около неподвижной горизонтальной оси под действием собственного веса.

Выбрав за плоскость xy (рис.2) вертикальную плоскость, в которой движется центр тяжести С тела, и определяя положение маятника углом φ, составляемым радиусом вращения центра тяжести с нисходящей вертикалью Ох, получаем уравнение вращения маятника в виде:

(12)

где а=ОС обозначен радиус вращения центра тяжести, а m – масса маятника. Если уравнению (12) придать вид:

где

(13)

то оно будет тождественно с уравнением (1) движения кругового математического маятника. Потому длину l, определяемую формулой , называют приведенной длиной физического маятника или длиной эквивалентного, т.е. имеющего тот же период колебаний, математического маятника.

Так как , где - момент инерции около центральной оси, параллельной оси вращения, то , т.е. l>a. Точка О' , лежащая на радиусе вращения центра тяжести на расстоянии l от оси вращения, называется центром качания, а прямая О'z',проходящая через центр качания параллельно оси вращения, - осью качания. Расстояние а'=О'С от оси качания до центра тяжести определяется по формуле , из которой следует, что если ось качания сделать осью вращения, то новой осью качания окажется старая ось вращения.

Порядок выполнения работы

Внимание! Во избежание получения травм и повреждения установки запрещается останавливать колебания маятника рукой.

Задание 1. Для нескольких конфигураций физического маятника измерить период колебаний при различных углах первоначального отклонения. Сравнить результаты измерений с теоретически рассчитанными. Данные, необходимые для расчета моментов инерции: масса стержня маятника 130 г, дискового груза 61 г, крепежного винта с гайкой – 1,5 г.