
- •Лекции по курсу «Электродинамика и распространение радиоволн»
- •Лекция 1. Вводная информация, основные понятия, история. Положения векторной алгебры
- •Название курса, преподаватель
- •Объем курса количество лекций, расписание, итоговая проверка
- •Рекомендуемая литература
- •Назначение курса. Рассматриваемые сущности
- •История
- •Рассматриваемые вопросы
- •Скаляры и векторы. Изображение векторов. Примеры скалярных и векторных величин
- •Операции над векторами. Скалярное, векторное, смешанное произведение
- •Скалярные и векторные поля. Изображение полей. Примеры скалярных и векторных полей
- •Лекция 2. Используемые понятия и законы векторного анализа. Заряды и токи. Векторы электромагнитного поля.
- •Циркуляция вектора и поток вектора через поверхность
- •Потенциальное и вихревое поле
- •Градиент, оператор Гамильтона
- •Дивергенция, физический смысл дивергенции
- •Ротор, физический смысл ротора
- •Теорема Стокса
- •Теорема Остроградского-Гаусса
- •Заряды, плотность заряда. Закон сохранения заряда
- •Ток, плотность тока
- •Векторы электромагнитного поля
- •Вектор е напряженности электрического поля.
- •Вектор магнитной индукции b
- •Векторы н и Dэлектромагнитного поля
- •Сводка векторов и их единиц измерения
- •Лекция 3. Основные законы электромагнетизма. Параметры сред. Уравнения Максвелла. В дифференциальной и интегральной форме
- •Закон Гаусса
- •Закон электромагнитной индукции (Фарадея)
- •Закон полного тока (Ампера)
- •Параметры сред, классификация сред
- •Уравнения Максвелла
- •Первое уравнение Максвелла. Ток смещения
- •Второе уравнение Максвелла
- •Третье уравнение Максвелла
- •Четвертое уравнение Максвелла
- •Лекция 4. Обсуждение уравнение Максвелла и следствий из них. Сторонние силы Метод комплексных амплитуд, применение к уравнениям Максвелла. Энергетические соотношения
- •Обсуждение уравнений Максвелла
- •Сторонние токи и заряды
- •Частные случаи электромагнитных процессов
- •Метод комплексных амплитуд
- •Уравнения Максвелла в комплексной форме
- •Комплексные диэлектрическая и магнитная проницаемость
- •Энергетические соотношения в электромагнитном поле. Теорема Пойнтинга
- •Теорема Пойнтинга для комплексных амплитуд
- •Лекция 5.
- •Уравнения Гельмгольца. Волновой характер электромагнитного поля
- •Волновые процессы
- •Плоские волны
- •Сферические волны
- •Цилиндрические волны
- •Плоская электромагнитная волна с линейной поляризацией
- •Фазовая скорость и постоянная затухания плоских волн
- •Плоские волны в хорошо проводящих средах
- •Лекция 6
- •Групповая скорость. Дисперсия
- •Групповая скорость
- •Поляризация электромагнитных волн
- •Линейная поляризация
- •Суперпозиция двух линейно поляризованных волн
- •Граничные условия для векторов электромагнитного поля
- •Граничные условия для нормальных составляющих магнитного поля
- •Граничные условия для нормальных составляющих электрического поля
- •Граничные условия для тангенциальных составляющих магнитного поля
- •Граничные условия для тангенциальных составляющих электрического поля
- •Сводка граничных условий
- •Лекция 7
- •Падение плоских электромагнитных волн на границу раздела двух сред
- •Плоские волны, распространяющиеся в произвольном направлении
- •Нормальное падение электромагнитной волны на идеально проводящую плоскость
- •Нормальное падение плоской электромагнитной волны на диэлектрическое полупространство
- •Падение плоской электромагнитной волны на диэлектрическое полупространство под произвольным углом
- •Лекция 8
- •Наклонное падение на границу раздела двух сред при перпендикулярной (горизонтальной) поляризации
- •Наклонное падение на границу раздела двух сред при параллельной (вертикальной) поляризации
- •Полное прохождение. Угол Брюстера
- •Полное отражение
- •Направляющие системы
Вектор е напряженности электрического поля.
На токи и заряды в электромагнитом поле
действуют силы. Механические силы,
действующие в поле на заряженные тела,
определяются векторами напряженности
электрического поля
![]() и магнитной индукции
и магнитной индукции![]() .
.
На электрический заряд q,
движущийся в электромагнитном поле со
скоростью![]() ,
действует сила как со стороны
электрического, так и со стороны
магнитного полей:
,
действует сила как со стороны
электрического, так и со стороны
магнитного полей:
![]()
![]() .
.
Хотя электромагнитное поле и характеризуется неразрывно связанными электрическим и магнитным полем, удобно рассмотреть воздействие этих сил на заряд по отдельности.
Первая сила относится к вектору
напряженности электрического поля
![]() .
Пусть заряд неподвижен,
.
Пусть заряд неподвижен,![]() .
Тогда механическая сила, действующая
на заряд в электрическом поле, определяется
как:
.
Тогда механическая сила, действующая
на заряд в электрическом поле, определяется
как:
![]() ,
,
и называется в силой Кулона, измеряется, как и всякая сила, в ньютонах. Отсюда следует:
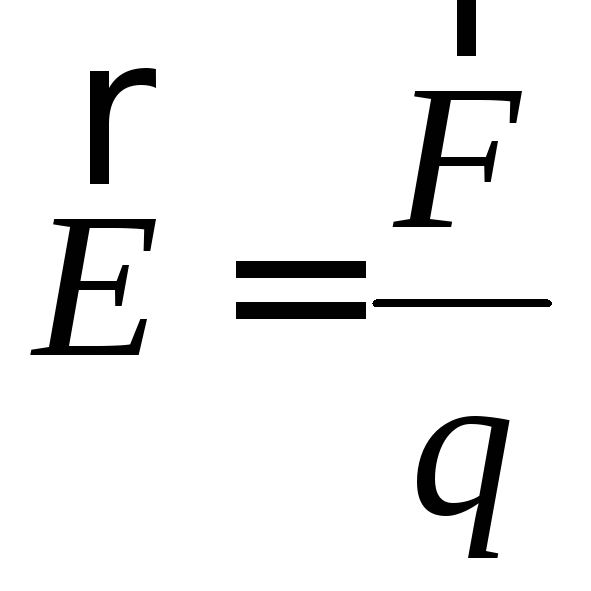 .
.
При заряде, равном одному кулону
![]() получим
получим
 .
.
Итак, вектор напряженности электрического
поля
![]() − отношение силы, действующей со стороны
электрического поля на неподвижный
электрический заряд, к величине этого
заряда. Или: вектор
− отношение силы, действующей со стороны
электрического поля на неподвижный
электрический заряд, к величине этого
заряда. Или: вектор![]() определяет величину и направление силы,
с которой электрическое поле действует
на заряд величиной
определяет величину и направление силы,
с которой электрическое поле действует
на заряд величиной![]() ,
помещенный в данной точке поля.
,
помещенный в данной точке поля.
Направление силы, действующей на тестовый
заряд
![]() ,
помещенный в поле зарядаq,
определяется по закону Кулона: если
зарядqположителен
– то вектор
,
помещенный в поле зарядаq,
определяется по закону Кулона: если
зарядqположителен
– то вектор![]() направлен от него (одноименные заряды
отталкиваются), если зарядqотрицателен – то вектор
направлен от него (одноименные заряды
отталкиваются), если зарядqотрицателен – то вектор![]() направлен к нему. Направление вектора
направлен к нему. Направление вектора![]() ,
как следует из его определения, совпадает
с направлением вектора силы
,
как следует из его определения, совпадает
с направлением вектора силы![]() (рисунок Рисунок 22 ).
(рисунок Рисунок 22 ).

−Взаимодействие зарядов и вектор напряженности электрического поля
Одиночный точечный заряд создает напряженность поля, равную
 ,
,
где
![]() −
единичный вектор, направленный от
заряда,
−
единичный вектор, направленный от
заряда,![]() − расстояние от заряда. Величина
− расстояние от заряда. Величина![]() называется абсолютной диэлектрической
проницаемостью и равна
называется абсолютной диэлектрической
проницаемостью и равна![]() .
.
Единицей измерения вектора
![]() является вольт/метр, В/м.
является вольт/метр, В/м.
Вектор магнитной индукции b
Рассмотрим теперь заряд q, движущийся в электромагнитном поле. Сила, с которой магнитное поле действует на этот заряд, определяется вторым слагаемым из общей силы:
![]() ,
,
и называется силой Лоренца (рисунок Рисунок 23 ).

−Заряд, движущийся в магнитном поле
. Отсюда видно, что магнитное поле
оказывает действие только на движущийся
заряд. Из определения векторного
произведения следует, что сила
![]() будет максимальна, если заряд перемещается
перпендикулярно магнитному полю:
будет максимальна, если заряд перемещается
перпендикулярно магнитному полю:
![]() ,
,
![]()
Единица измерения вектора
![]() − тесла, при
− тесла, при![]() и
и![]() м/с
м/с
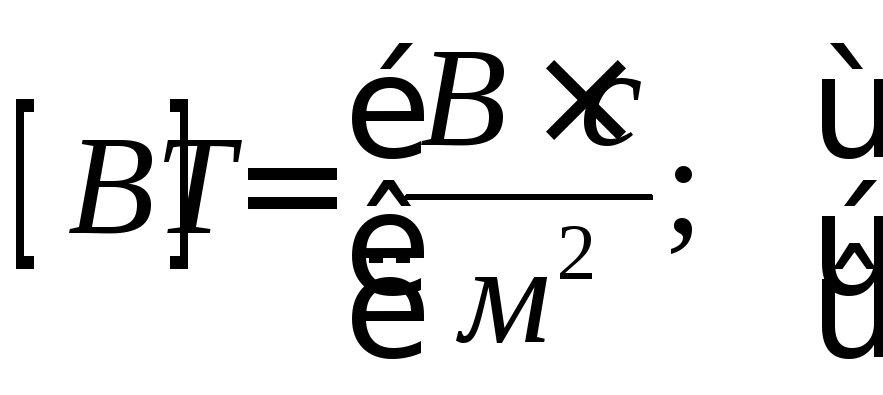 .
.
Сила Лоренца не изменяет скорости
движения заряда и его энергии; она
создает ускорение, изменяя траекторию
движения заряда. Например, при движении
положительного заряда перпендикулярно
однородному магнитному полю возникает
центростремительная сила, перпендикулярная
вектору
![]() ,
которая заставляет заряд двигаться по
окружности постоянного радиуса, как
показано на рисунке Рисунок 24 .
,
которая заставляет заряд двигаться по
окружности постоянного радиуса, как
показано на рисунке Рисунок 24 .
На этом рисунке используется еще один способ представления векторов, направленных перпендикулярно плоскости рисунка. При этом вектор, направленный от рисунка к зрителю, обозначается кружком с точкой, а от зрителя к рисунку – кружком с перекрестием. Здесь используется зрительная аналогия со стрелой: кружок с точкой представляет собой острие стрелы, а кружок с перекрестием – оперение стрелы; по ним можно определить направление полета.
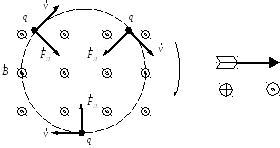
−Вращение заряда в магнитном поле
Можно сказать, что заряды «захватываются» магнитным полем – это свойство магнитного поля используется в электронных приборах: для отклонения пучка электронов в электронно-лучевых трубках и других устройствах.
