
- •Лекции по курсу «Электродинамика и распространение радиоволн»
- •Лекция 1. Вводная информация, основные понятия, история. Положения векторной алгебры
- •Название курса, преподаватель
- •Объем курса количество лекций, расписание, итоговая проверка
- •Рекомендуемая литература
- •Назначение курса. Рассматриваемые сущности
- •История
- •Рассматриваемые вопросы
- •Скаляры и векторы. Изображение векторов. Примеры скалярных и векторных величин
- •Операции над векторами. Скалярное, векторное, смешанное произведение
- •Скалярные и векторные поля. Изображение полей. Примеры скалярных и векторных полей
- •Лекция 2. Используемые понятия и законы векторного анализа. Заряды и токи. Векторы электромагнитного поля.
- •Циркуляция вектора и поток вектора через поверхность
- •Потенциальное и вихревое поле
- •Градиент, оператор Гамильтона
- •Дивергенция, физический смысл дивергенции
- •Ротор, физический смысл ротора
- •Теорема Стокса
- •Теорема Остроградского-Гаусса
- •Заряды, плотность заряда. Закон сохранения заряда
- •Ток, плотность тока
- •Векторы электромагнитного поля
- •Вектор е напряженности электрического поля.
- •Вектор магнитной индукции b
- •Векторы н и Dэлектромагнитного поля
- •Сводка векторов и их единиц измерения
- •Лекция 3. Основные законы электромагнетизма. Параметры сред. Уравнения Максвелла. В дифференциальной и интегральной форме
- •Закон Гаусса
- •Закон электромагнитной индукции (Фарадея)
- •Закон полного тока (Ампера)
- •Параметры сред, классификация сред
- •Уравнения Максвелла
- •Первое уравнение Максвелла. Ток смещения
- •Второе уравнение Максвелла
- •Третье уравнение Максвелла
- •Четвертое уравнение Максвелла
- •Лекция 4. Обсуждение уравнение Максвелла и следствий из них. Сторонние силы Метод комплексных амплитуд, применение к уравнениям Максвелла. Энергетические соотношения
- •Обсуждение уравнений Максвелла
- •Сторонние токи и заряды
- •Частные случаи электромагнитных процессов
- •Метод комплексных амплитуд
- •Уравнения Максвелла в комплексной форме
- •Комплексные диэлектрическая и магнитная проницаемость
- •Энергетические соотношения в электромагнитном поле. Теорема Пойнтинга
- •Теорема Пойнтинга для комплексных амплитуд
- •Лекция 5.
- •Уравнения Гельмгольца. Волновой характер электромагнитного поля
- •Волновые процессы
- •Плоские волны
- •Сферические волны
- •Цилиндрические волны
- •Плоская электромагнитная волна с линейной поляризацией
- •Фазовая скорость и постоянная затухания плоских волн
- •Плоские волны в хорошо проводящих средах
- •Лекция 6
- •Групповая скорость. Дисперсия
- •Групповая скорость
- •Поляризация электромагнитных волн
- •Линейная поляризация
- •Суперпозиция двух линейно поляризованных волн
- •Граничные условия для векторов электромагнитного поля
- •Граничные условия для нормальных составляющих магнитного поля
- •Граничные условия для нормальных составляющих электрического поля
- •Граничные условия для тангенциальных составляющих магнитного поля
- •Граничные условия для тангенциальных составляющих электрического поля
- •Сводка граничных условий
- •Лекция 7
- •Падение плоских электромагнитных волн на границу раздела двух сред
- •Плоские волны, распространяющиеся в произвольном направлении
- •Нормальное падение электромагнитной волны на идеально проводящую плоскость
- •Нормальное падение плоской электромагнитной волны на диэлектрическое полупространство
- •Падение плоской электромагнитной волны на диэлектрическое полупространство под произвольным углом
- •Лекция 8
- •Наклонное падение на границу раздела двух сред при перпендикулярной (горизонтальной) поляризации
- •Наклонное падение на границу раздела двух сред при параллельной (вертикальной) поляризации
- •Полное прохождение. Угол Брюстера
- •Полное отражение
- •Направляющие системы
Поляризация электромагнитных волн
При рассмотрении плоской волны в
однородной изотропной среде было
показано, что она является поперечной,
т.е. векторы
![]() и
и![]() перпендикулярны направлению распространения
(оси
перпендикулярны направлению распространения
(оси![]() ).
В целях упрощения полагалось, что вектор
).
В целях упрощения полагалось, что вектор![]() ориентирован вдоль оси
ориентирован вдоль оси![]() ,
и было установлено, что в этом случае
вектор
,
и было установлено, что в этом случае
вектор![]() ориентирован по оси
ориентирован по оси![]() (рисунок Рисунок 50 ).
(рисунок Рисунок 50 ).
−Простейший случай линейно поляризованной волны
![]() ,
,
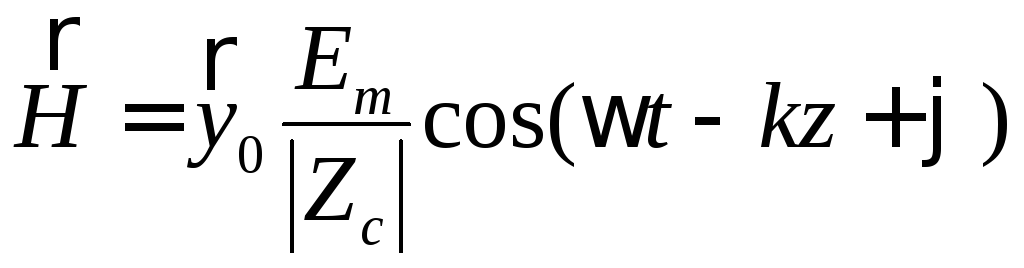 .
.
Однако следует иметь в виду, что ориентация
векторов
![]() и
и![]() относительно координатных осей зависит
от источника, создающего волну. В общем
случае направления векторов могут
отличаться от направления координатных
осей, а значит, каждый из векторов поля
может иметь составляющие по обеим
координатным осям, причем начальные
фазы составляющих могут отличаться.
Это приводит к тому, что положение
вектора
относительно координатных осей зависит
от источника, создающего волну. В общем
случае направления векторов могут
отличаться от направления координатных
осей, а значит, каждый из векторов поля
может иметь составляющие по обеим
координатным осям, причем начальные
фазы составляющих могут отличаться.
Это приводит к тому, что положение
вектора![]() в пространстве будет отличаться от
простейшего случая, когда этот вектор
всегда колеблется в плоскости
в пространстве будет отличаться от
простейшего случая, когда этот вектор
всегда колеблется в плоскости![]() .
.
Поляризация электромагнитной волы −
ориентация в пространстве вектора
напряженности электрического поля
![]() .
.
Различают три вида поляризации: линейную, круговую и эллиптическую. Как будет показано, все эти три вида являются частными случаями общего эллиптического представления.
Линейная поляризация
Простейшим случаем является линейная
поляризация. Если рассмотреть выражение
для вектора
![]() :
:
![]() ,
,
то окажется, что половину периода
направление вектора
![]() совпадает с положительным направлением
оси
совпадает с положительным направлением
оси![]() ,
а вторую половину − противоположно ему
(рисунок Рисунок 51 ). Таким образом, в
фиксированной точке пространства
,
а вторую половину − противоположно ему
(рисунок Рисунок 51 ). Таким образом, в
фиксированной точке пространства![]() конец вектора
конец вектора![]() с течением времени перемещается вдоль
отрезка прямой линии, а величина вектора
изменяется в интервале
с течением времени перемещается вдоль
отрезка прямой линии, а величина вектора
изменяется в интервале![]() .
Волны, имеющие такой характер ориентации
вектора
.
Волны, имеющие такой характер ориентации
вектора![]() ,
называются линейно поляризованными.
Плоскость, проходящую через направление
распространение волны и вектор
,
называются линейно поляризованными.
Плоскость, проходящую через направление
распространение волны и вектор![]() ,
называют плоскостью поляризации. В
рассматриваемом примере плоскостью
поляризации является плоскость
,
называют плоскостью поляризации. В
рассматриваемом примере плоскостью
поляризации является плоскость![]() .
.

−Электромагнитная волна с линейной поляризацией
Линейная поляризация исключительно часто применяется в антенной технике. Так, все местное (не спутниковое) теле- и радиовещание производится на радиоволнах линейной поляризации. Положение плоскости поляризации полностью определяется ориентацией приемных и передающих антенн. Так как плоскостью линейной поляризации может быть как плоскость параллельная земной поверхности, так и перпендикулярная ей, то обычно их называют соответственно горизонтальной и вертикальной плоскостью поляризации. Так, телевещание обычно производится в горизонтальной плоскости поляризации, а радиовещание − в вертикальной, хотя бывают и исключения.
Суперпозиция двух линейно поляризованных волн
Предположим теперь, что волна создается
более сложной излучающей структурой и
вектор
![]() имеет две составляющие
имеет две составляющие![]() и
и![]() ,
которые изменяются либо синфазно, либо
с некоторым фазовым сдвигом. Вектор
,
которые изменяются либо синфазно, либо
с некоторым фазовым сдвигом. Вектор![]() в этом случае тоже имеет две составляющие
в этом случае тоже имеет две составляющие![]() и
и![]() ,
связанные с компонентами
,
связанные с компонентами![]() .
Тогда в общем случае выражение для
вектора
.
Тогда в общем случае выражение для
вектора![]() плоской волны в среде без потерь
записывается в виде
плоской волны в среде без потерь
записывается в виде
![]() ,
,
где
![]() и
и![]() − амплитуды составляющих
− амплитуды составляющих![]() и
и![]() соответственно, а
соответственно, а![]() и
и![]() − фазы этих составляющих в точке
− фазы этих составляющих в точке![]() при
при![]() .
Волну такого типа можно рассматривать
как суперпозицию двух плоских линейно
поляризованных волн со взаимно
перпендикулярными плоскостями поляризации
.
Волну такого типа можно рассматривать
как суперпозицию двух плоских линейно
поляризованных волн со взаимно
перпендикулярными плоскостями поляризации![]() и
и![]() ,
распространяющихся в одном направлении
вдоль оси
,
распространяющихся в одном направлении
вдоль оси![]() .
Характер изменения вектора
.
Характер изменения вектора![]() с течением времени в фиксированной
точке пространства зависит от соотношения
между начальными фазами
с течением времени в фиксированной
точке пространства зависит от соотношения
между начальными фазами![]() ,
,![]() и от амплитуд
и от амплитуд![]() ,
,![]() .
.
Рассмотрим, что произойдет при отдельных
частных случаях такой волны. Для этого
рассмотрим угол между осью
![]() и вектором
и вектором![]() в некоторой фиксированной точке
пространства
в некоторой фиксированной точке
пространства![]() .
Очевидно, что величина этого угла зависит
от соотношения между мгновенными
значениями компонент вектора
.
Очевидно, что величина этого угла зависит
от соотношения между мгновенными
значениями компонент вектора![]() (рисунок Рисунок 52 ):
(рисунок Рисунок 52 ):
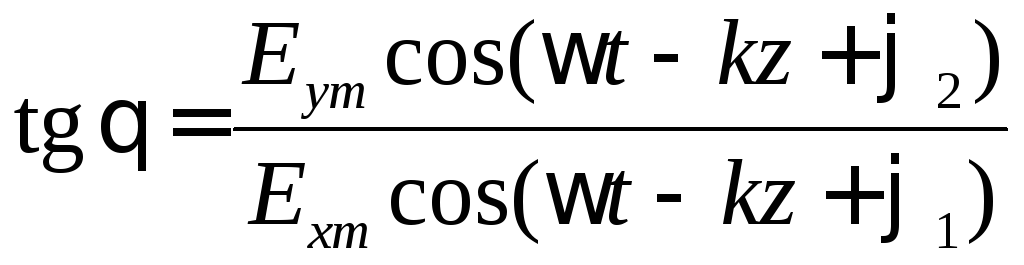 ,
,
то есть,
![]() зависит от соотношения величин
зависит от соотношения величин![]() ,
,![]() и
и![]() ,
,![]() и в общем случае меняется со временем.
Для получения случая линейной поляризации
необходимо, чтобы составляющие вектора
и в общем случае меняется со временем.
Для получения случая линейной поляризации
необходимо, чтобы составляющие вектора![]() были синфазными или противофазными.
Положим сначала
были синфазными или противофазными.
Положим сначала![]() ,
тогда
,
тогда
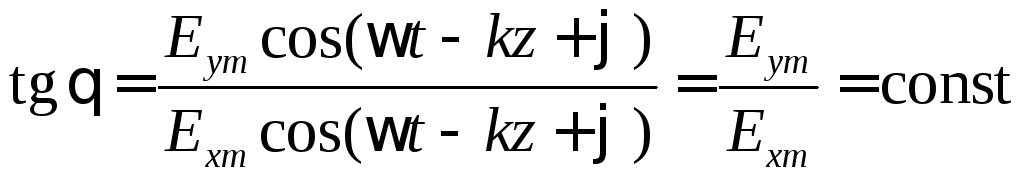 .
.
В этом случае вектор
![]() в любой момент времени лежит в плоскости,
проходящей через ось
в любой момент времени лежит в плоскости,
проходящей через ось![]() и составляющей угол
и составляющей угол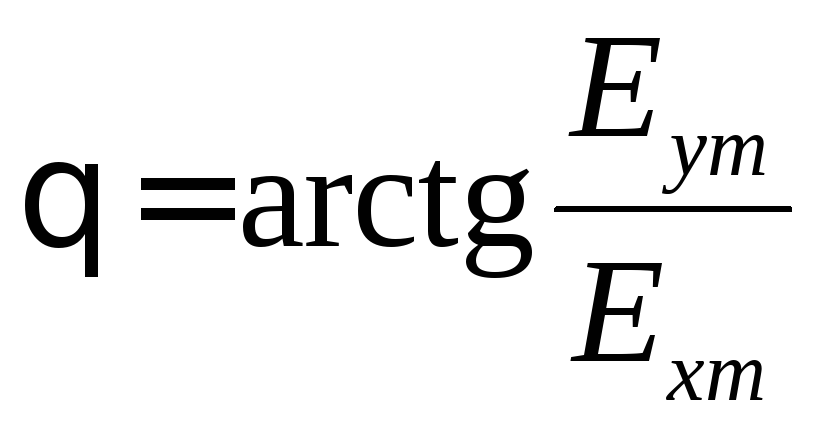 с плоскостью
с плоскостью![]() .
.

−Линейно поляризованная волна
Аналогичное явление имеет место также
в том случае, когда разность между
начальными фазами равна целому числу
![]() :
:
![]() ,
где
,
где![]()
Очевидно, что при
![]() или
или![]() линейно поляризованная волна превращается
в волну с чисто горизонтальной или чисто
вертикальной поляризацией.
линейно поляризованная волна превращается
в волну с чисто горизонтальной или чисто
вертикальной поляризацией.

− Горизонтальная и вертикальная поляризация
Рассмотрим второй частный случай. Пусть
амплитуды составляющих
![]() и
и![]() равны, а начальные фазы отличаются на
равны, а начальные фазы отличаются на![]() :
:
![]() ,
,
![]()
Тогда
![]() ,
,
![]()
Подставляя эти значения в выражение
для угла
![]() ,
получим:
,
получим:
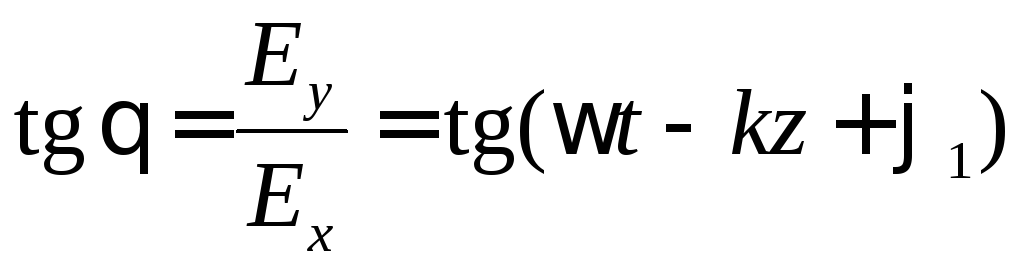 ,
,
откуда следует, что
![]() ,
,
где
![]() − целое число. Это равенство означает,
что угол
− целое число. Это равенство означает,
что угол![]() в фиксированной точке пространства
в фиксированной точке пространства![]() увеличивается с течением времени.
Величина вектора
увеличивается с течением времени.
Величина вектора![]() при этом остается неизменной:
при этом остается неизменной:
![]() .
.
Таким образом, в фиксированной точке
пространства вектор
![]() ,
оставаясь неизменным по величине,
вращается с угловой частотой
,
оставаясь неизменным по величине,
вращается с угловой частотой![]() вокруг направления оси
вокруг направления оси![]() .
Конец вектора при этом описывает
окружность (рисунок Рисунок 54 ). Волны
такого типа называются волнами с круговой
поляризацией.
.
Конец вектора при этом описывает
окружность (рисунок Рисунок 54 ). Волны
такого типа называются волнами с круговой
поляризацией.

−Круговая поляризация плоской волны
Нетрудно убедиться также, что волна
будет иметь круговую поляризацию не
только в случае
![]() ,
но и
,
но и
![]() ,
,
где
![]() .
.
Вдоль направления распространения
(вдоль оси
![]() )
в фиксированный момент времени
)
в фиксированный момент времени![]() в среде без потерь конец вектора
в среде без потерь конец вектора![]() описывает винтовую линию с шагом, равным
длине волны. Проекция этой линии на
плоскость
описывает винтовую линию с шагом, равным
длине волны. Проекция этой линии на
плоскость![]() образует окружность. С течением времени
эта винтовая линия перемещается вдоль
оси
образует окружность. С течением времени
эта винтовая линия перемещается вдоль
оси![]() по цилиндру с фазовой скоростью
по цилиндру с фазовой скоростью![]() .
.
В зависимости от направления вращения
вектора вокруг оси распространения
различают волны с левой и правой круговой
поляризацией. В случае правой поляризации
вектор
![]() вращается по часовой стрелке, если
смотреть вдоль направления распространения,
а в случае левой круговой поляризации
− против стрелки. В рассмотренном
примере при
вращается по часовой стрелке, если
смотреть вдоль направления распространения,
а в случае левой круговой поляризации
− против стрелки. В рассмотренном
примере при![]() волна имеет правую поляризацию. Очевидно,
что такая же поляризация будет в случае
волна имеет правую поляризацию. Очевидно,
что такая же поляризация будет в случае
![]() ,
,![]() .
.
В случае
![]() ,
,![]()
волна имеет левую круговую поляризацию.
Вектор
![]() однородной волны везде и в любой момент
времени перпендикулярен вектору
однородной волны везде и в любой момент
времени перпендикулярен вектору![]() и пропорционален ему по величине. Таким
образом, в отличие от линейной поляризации,
поле бегущей волны с круговой поляризацией
в любой момент времени ни в одной точке
пространства не равно нулю.
и пропорционален ему по величине. Таким
образом, в отличие от линейной поляризации,
поле бегущей волны с круговой поляризацией
в любой момент времени ни в одной точке
пространства не равно нулю.
В случае среды с потерями линия,
соединяющая концы векторов в один м тот
же момент времени в разных точках оси
![]() ,
представляет собой спираль с радиусом,
который изменяется вдоль оси по закону
,
представляет собой спираль с радиусом,
который изменяется вдоль оси по закону![]() .
.
В самом общем случае распространения
волны, когда
![]() конец вектора
конец вектора![]() будет описывать при фиксированном
будет описывать при фиксированном
![]() и переменном
и переменном![]() в пространстве некий эллипс (рисунок
Рисунок 55 ). Полуоси эллипса в общем
случае не совпадают с осями координат.
в пространстве некий эллипс (рисунок
Рисунок 55 ). Полуоси эллипса в общем
случае не совпадают с осями координат.

−Эллиптически поляризованная волна
Для определения эллиптичности поля используется коэффициент эллиптичности, характеризующий отношение малой полуоси эллипса к большой:
![]() .
.
При
![]() эллипс вырождается в окружность, этот
случай соответствует электромагнитной
волне с круговой поляризацией. Если
эллипс вырождается в окружность, этот
случай соответствует электромагнитной
волне с круговой поляризацией. Если![]() ,
то эллипс вырождается в прямую линию −
это линейно поляризованная волна.
,
то эллипс вырождается в прямую линию −
это линейно поляризованная волна.
При рассмотрении эллиптической и круговой поляризаций нами рассматривалась суперпозиция двух линейно поляризованных волн. Как мы увидели, поле с любым типом поляризации можно представить суммой двух волн, поляризованных линейно в двух ортогональных плоскостях. Можно доказать и обратное: эллиптически или линейно поляризованную волну можно представить в виде суммы двух волн с круговой поляризацией и противоположными направлениями вращения.
