7. Фазовая скорость и постоянная затухания плоских волн

В данном разделе на основе приведенных общих положений мы получим характеристики распространения плоских электромагнитных волн в некоторых наиболее важных средах.

Вакуум. Фазовая скорость волн в вакууме находится по общей формуле

.

Поскольку фазовая постоянная волн в вакууме

,

фазовая скорость определится как

.

Таким образом, получен один из основных результатов теории Максвелла − отождествление скорости света в вакууме со скоростью произвольной электромагнитной волны. Другими словами, скорость плоских электромагнитных волн в вакууме равна скорости света независимо от частоты этих волн. В физике среды с подобными свойствами носят название сред без дисперсии.

Диэлектрик без потерь. Рассматривая случай немагнитного диэлектрика с , что часто встречается на практике, будем иметь

.

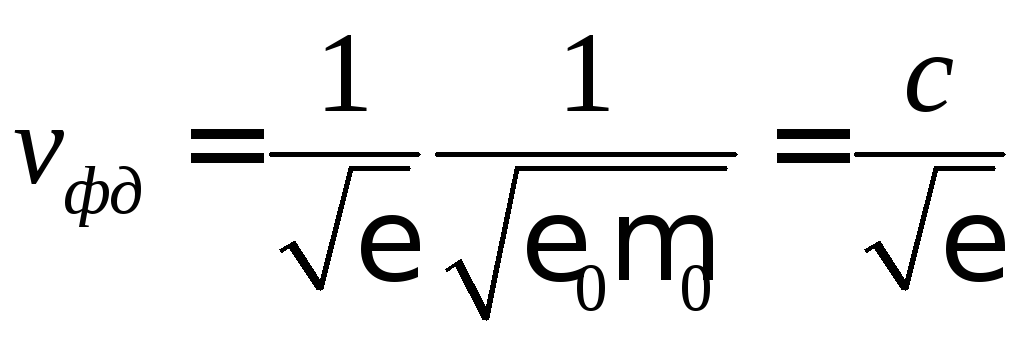Таким образом, фазовая скорость, а следовательно, и длина волны в диэлектрике уменьшаются в раз по сравнению с аналогичными величинами, вычисленными для вакуума:

.

Диэлектрик с потерями. Для анализа распространения волн в данной среде нужно воспользоваться понятием комплексной диэлектрической проницаемости

,

где

,.

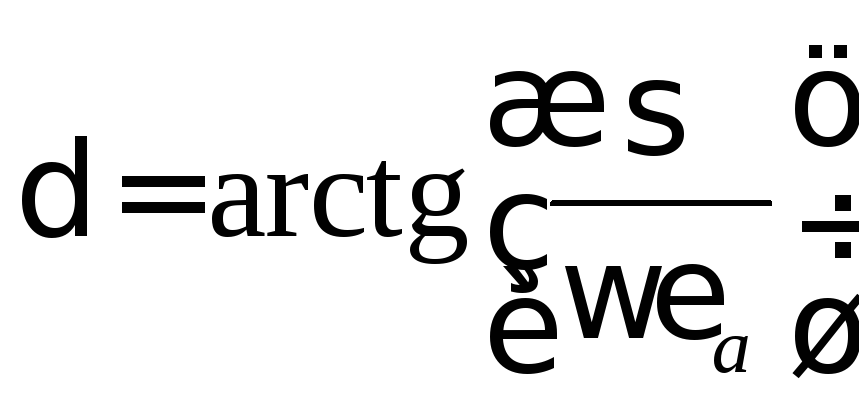Комплексная постоянная распространения в этом случае запишется следующим образом:

.

Поскольку , раскрывая это выражение по формуле Эйлера, будем иметь значение фазовой постоянной

и постоянной затухания

.

Как уже указывалось, реальные диэлектрики характеризуются весьма малыми углами потерь, порядка , в силу чего с точностью до величин порядкаможно считать, что

,,.

Отсюда

,

,

.

Вывод, следующий из этих формул, состоит в том, что при расчете фазовых соотношений в первом приближении можно не учитывать потерь в материале. С другой стороны, коэффициент затухания плоских волн в неидеальном диэлектрике прямо пропорционален углу диэлектрических потерь.

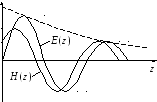
47. − Плоская волна в среде с потерями

8. Плоские волны в хорошо проводящих средах

Вопрос о распространении плоских волн в реальных металлах и металлоподобных средах рассмотрим более подробно из-за его практической важности. По определению с электродинамической точки зрения среда является хорошо проводящей, т.е., металлоподобной, если в каждой точке ее плотность токов проводимости значительно превосходит плотность токов смещения. Это же условие металлоподобности может быть сформулировано в виде

, т.е., мнимая часть комплексной диэлектрической проницаемости должна значительно превосходить вещественную часть.

Очевидно, что чем ниже частота , тем ближе при прочих равных условиях приближается данная среда к идеальному металлу. На достаточно низких частотах многие среды, известные как диэлектрики, становятся металлоподобными. Например, для сухой почвы с параметрами,на частоте 1 МГц имеем,. Таким образом, на частотах радиовещательных диапазонов сухая почва ведет себя подобно металлу. Такое свойство в ряде случаев позволяет значительно упростить решение практических задач.

Согласно сделанному предположению, комплексную диэлектрическую проницаемость металлоподобной среды можно считать мнимой:

.

Найдем комплексную постоянную распространения плоских электромагнитных волн в такой среде. По общему правилу,

.

Поскольку , то выражение можно переписать в виде

.

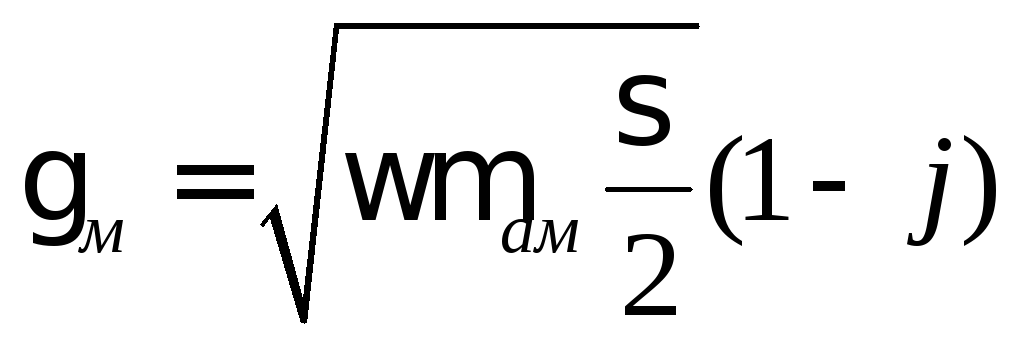Итак,

.

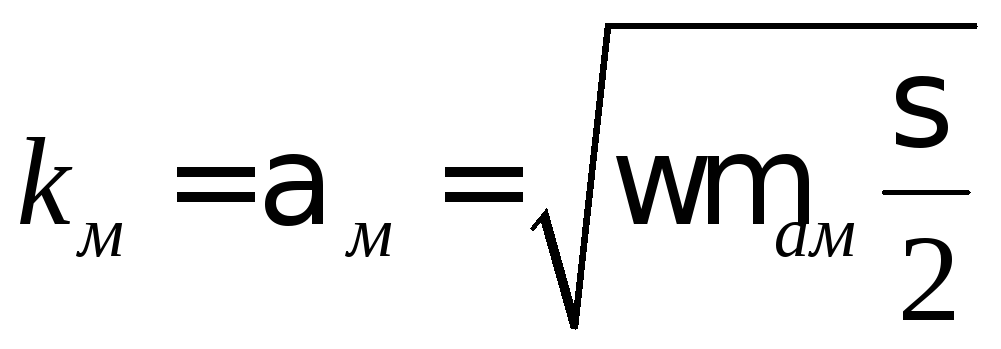Отсюда можно вычислить длину волны в хорошо проводящей среде:

.

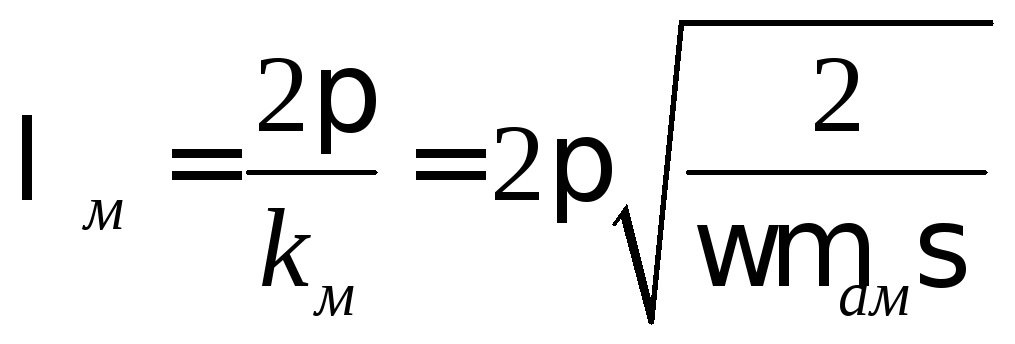Интересно отметить, что длина волны в металле значительно сокращается по сравнению с длиной волны в свободном пространстве. Действительно, легко вычислить, что

.

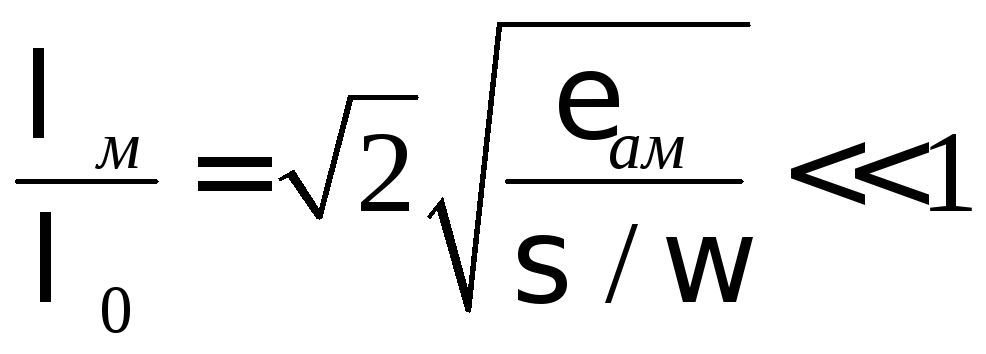Согласно этому неравенству, в металле значительно снижается фазовая скорость плоских электромагнитных волн.

Как известно, амплитуда электромагнитных волн в среде с потерями уменьшается по закону . Расстояние, на котором амплитуда электромагнитных волн падает в е раз по сравнению с ее начальным уровнем, называется глубиной проникновения или глубиной поверхностного слоя (скин-слоя). Эта величина удовлетворяет соотношению

.

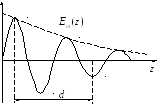
48. − Глубина проникновения

Пользуясь вышеприведенными соотношениями, будем иметь

.

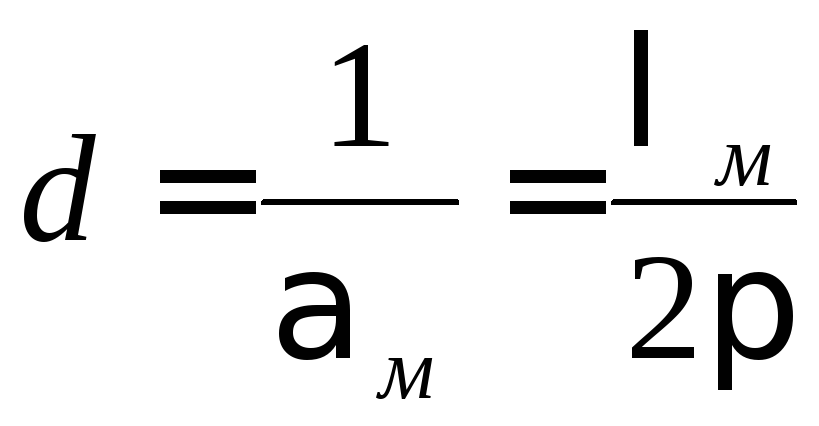Таким образом, приходим к другому определению: металлоподобной называется среда, в которой поле затухает на расстоянии, меньшем одной длины волны. Формула для вычисления глубины поверхностного слоя имеет следующий вид:

,

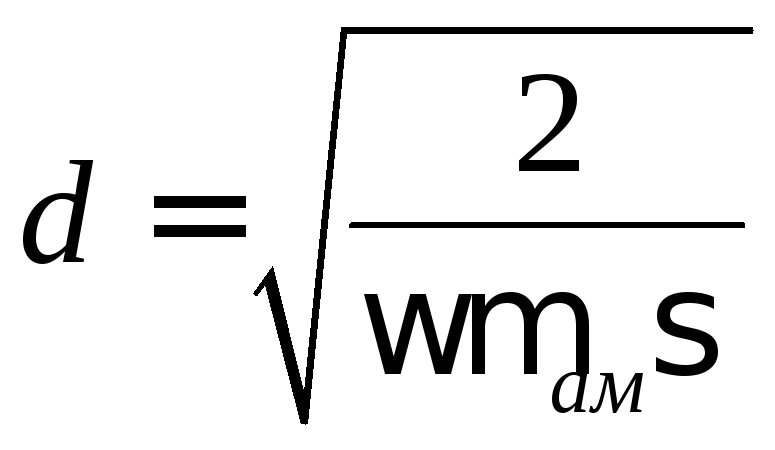т.е., глубина проникновения электромагнитных волн в металл уменьшается с ростом частоты и его удельной объемной проводимости.

Конкретный расчет по этой формуле показывает, что для металлов на частотах СВЧ диапазона величина оказывается весьма малой. Так, для меди, у которой, на частоте 10 ГГц (длина волны 3 см) имеем. Отсюда следует важный для практики вывод об использовании нанесенного на поверхность конструкции слоя хорошо проводящего вещества, например серебра толщиной порядка 0,01 мм. Такое проводящее покрытие позволяет просто и дешево выполнять элементы СВЧ устройств с малыми тепловыми потерями.