
- •Лекции по курсу «Электродинамика и распространение радиоволн»
- •Лекция 1. Вводная информация, основные понятия, история. Положения векторной алгебры
- •Название курса, преподаватель
- •Объем курса количество лекций, расписание, итоговая проверка
- •Рекомендуемая литература
- •Назначение курса. Рассматриваемые сущности
- •История
- •Рассматриваемые вопросы
- •Скаляры и векторы. Изображение векторов. Примеры скалярных и векторных величин
- •Операции над векторами. Скалярное, векторное, смешанное произведение
- •Скалярные и векторные поля. Изображение полей. Примеры скалярных и векторных полей
- •Лекция 2. Используемые понятия и законы векторного анализа. Заряды и токи. Векторы электромагнитного поля.
- •Циркуляция вектора и поток вектора через поверхность
- •Потенциальное и вихревое поле
- •Градиент, оператор Гамильтона
- •Дивергенция, физический смысл дивергенции
- •Ротор, физический смысл ротора
- •Теорема Стокса
- •Теорема Остроградского-Гаусса
- •Заряды, плотность заряда. Закон сохранения заряда
- •Ток, плотность тока
- •Векторы электромагнитного поля
- •Вектор е напряженности электрического поля.
- •Вектор магнитной индукции b
- •Векторы н и Dэлектромагнитного поля
- •Сводка векторов и их единиц измерения
- •Лекция 3. Основные законы электромагнетизма. Параметры сред. Уравнения Максвелла. В дифференциальной и интегральной форме
- •Закон Гаусса
- •Закон электромагнитной индукции (Фарадея)
- •Закон полного тока (Ампера)
- •Параметры сред, классификация сред
- •Уравнения Максвелла
- •Первое уравнение Максвелла. Ток смещения
- •Второе уравнение Максвелла
- •Третье уравнение Максвелла
- •Четвертое уравнение Максвелла
- •Лекция 4. Обсуждение уравнение Максвелла и следствий из них. Сторонние силы Метод комплексных амплитуд, применение к уравнениям Максвелла. Энергетические соотношения
- •Обсуждение уравнений Максвелла
- •Сторонние токи и заряды
- •Частные случаи электромагнитных процессов
- •Метод комплексных амплитуд
- •Уравнения Максвелла в комплексной форме
- •Комплексные диэлектрическая и магнитная проницаемость
- •Энергетические соотношения в электромагнитном поле. Теорема Пойнтинга
- •Теорема Пойнтинга для комплексных амплитуд
- •Лекция 5.
- •Уравнения Гельмгольца. Волновой характер электромагнитного поля
- •Волновые процессы
- •Плоские волны
- •Сферические волны
- •Цилиндрические волны
- •Плоская электромагнитная волна с линейной поляризацией
- •Фазовая скорость и постоянная затухания плоских волн
- •Плоские волны в хорошо проводящих средах
- •Лекция 6
- •Групповая скорость. Дисперсия
- •Групповая скорость
- •Поляризация электромагнитных волн
- •Линейная поляризация
- •Суперпозиция двух линейно поляризованных волн
- •Граничные условия для векторов электромагнитного поля
- •Граничные условия для нормальных составляющих магнитного поля
- •Граничные условия для нормальных составляющих электрического поля
- •Граничные условия для тангенциальных составляющих магнитного поля
- •Граничные условия для тангенциальных составляющих электрического поля
- •Сводка граничных условий
- •Лекция 7
- •Падение плоских электромагнитных волн на границу раздела двух сред
- •Плоские волны, распространяющиеся в произвольном направлении
- •Нормальное падение электромагнитной волны на идеально проводящую плоскость
- •Нормальное падение плоской электромагнитной волны на диэлектрическое полупространство
- •Падение плоской электромагнитной волны на диэлектрическое полупространство под произвольным углом
- •Лекция 8
- •Наклонное падение на границу раздела двух сред при перпендикулярной (горизонтальной) поляризации
- •Наклонное падение на границу раздела двух сред при параллельной (вертикальной) поляризации
- •Полное прохождение. Угол Брюстера
- •Полное отражение
- •Направляющие системы
Волновые процессы
Как уже указывалось, переменное во времени электромагнитное поле носит волновой характер. Далее мы рассмотрим волновые процессы, происходящие в электромагнитном поле.
С самой общей точки зрения волнами называются колебательные движения непрерывных сред. Физическая природа волновых явлений чрезвычайно разнообразна. Так, известны электромагнитные волны, звуковые – акустические волны, волны на поверхности жидкости и т.д. Проведение всеобъемлющей классификации здесь весьма затруднительно. Для понимания структуры электромагнитных волн сравним между собой два хорошо известных и легко представимых волновых процесса − звуковые волны и волны на поверхности воды (рисунок Рисунок 41 ).
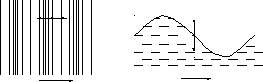
−Продольные и поперечные волны
Волны, показанные на рисунке, распространяются в направлении стрелок. Звуковые волны, представляющие собой перемещение в пространстве областей сгущения и разрежения газа, характеры тем, что в них каждая отдельная частица газа колеблется в направлении, совпадающем с направлением распространения волны. Такие волны носят название продольных волн. В литературе можно встретить также термины акустические или скалярные волны.
Совсем иной природой обладают волны на поверхности воды. Здесь колеблющиеся частицы перемещаются в направлении, перпендикулярном направлению распространения. Поэтому для волны данного вида недостаточно лишь указать величину смещения колеблющихся точек относительно положения равновесия, а следует указать конкретно ту плоскость, в которой происходят колебания. Эта плоскость называется плоскостью поляризации волны, а сам волновой процесс – поперечными, поляризованными или векторными волнами.
Можно доказать, и это будет видно из примеров, что электромагнитные волны имеют вид поперечных волн. Волны разной физической природы классифицируются в зависимости от того, какую конфигурацию они принимают в пространстве.
Плоские волны
Рассмотрим безграничное трехмерное
пространство с декартовой системой
координат, в каждой точке которого
задана некоторая величина
![]() ,
физическая природа которой безразлична.
Пусть эта величина во времени и
пространстве изменяется по закону
,
физическая природа которой безразлична.
Пусть эта величина во времени и
пространстве изменяется по закону
![]() .
.
При этом говорят, что в пространстве
существует монохроматическая плоская
волна. Аргумент косинуса, т.е.
![]() ,
называемый обычно фазой волны, является
функцией времени
,
называемый обычно фазой волны, является
функцией времени![]() и пространственной координаты
и пространственной координаты![]() .
Если зафиксировать
.
Если зафиксировать![]() ,
то величина
,
то величина![]() принимает те же самые значения через
промежутки времени, кратные периоду
принимает те же самые значения через
промежутки времени, кратные периоду![]() .
Если же фиксировано время, то величина
.
Если же фиксировано время, то величина![]() изменяется периодически вдоль оси
изменяется периодически вдоль оси![]() с периодом
с периодом![]() ,
называемом длиной волны. Легко видеть,
что величины
,
называемом длиной волны. Легко видеть,
что величины![]() и
и![]() связаны друг с другом:
связаны друг с другом:
![]() .
.
Величина
![]() служит важнейшей характеристикой
волнового процесса и носит название
постоянной распространения волны.
Употребляются также термины фазовая
постоянная и волновое число, а вместо
символа
служит важнейшей характеристикой
волнового процесса и носит название
постоянной распространения волны.
Употребляются также термины фазовая
постоянная и волновое число, а вместо
символа![]() используется
используется![]() .
Физический смысл волнового числа состоит
в том, что оно указывает, на сколько
радиан изменяется фаза волны при
прохождении одного метра пути.
.
Физический смысл волнового числа состоит
в том, что оно указывает, на сколько
радиан изменяется фаза волны при
прохождении одного метра пути.
Наличие двух возможных знаков в формуле, описывающей плоскую волну, связано с тем, что плоские волны могут распространяться в двух направлениях. Назовем поверхность, удовлетворяющую условию
![]() ,
,
волновым фронтом плоской волны. Очевидно,
что в рассматриваемом случае волновые
фронты представляют собой бесконечные
плоскости, перпендикулярные оси
![]() и перемещающиеся в пространстве со
скоростью
и перемещающиеся в пространстве со
скоростью
![]() ,
,
носящей название фазовой скорости. Фазовая скорость − это скорость, с которой должна перемещаться точка наблюдения, чтобы фаза поля в ней оставалась неизменной. Поскольку время изменяется всегда в одном направлении, то уравнение
![]()
соответствует фронту волны,
распространяющейся в направлении
положительной оси
![]() .
Изменение знака в фазе волны ведет к
изменению направления ее распространения.
.
Изменение знака в фазе волны ведет к
изменению направления ее распространения.
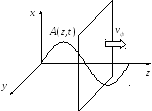
− Плоская волна
Введем комплексные амплитуды плоских волн. В соответствии с методом комплексных амплитуд будем иметь для волны, распространяющейся в положительном направлении
![]() ,
,
а для волны, идущей в противоположную сторону,
![]() .
.
Распространение волн в любой реальной
среде неизбежно сопровождается
уменьшением их амплитуды за счет тепловых
потерь. Закон затухания легко найти из
следующих простых соображений.
Предположим, что в начальной плоскости
![]() амплитуда волны имеет исходную величину
амплитуда волны имеет исходную величину![]() ,
условно принимаемую за 100%. Положим
далее, что при прохождении 1 м пути
амплитуда падает на 10%, т.е.
,
условно принимаемую за 100%. Положим
далее, что при прохождении 1 м пути
амплитуда падает на 10%, т.е.![]() .
Легко найти, что
.
Легко найти, что![]() ,
,![]() и т.д. Общая закономерность имеет вид
и т.д. Общая закономерность имеет вид
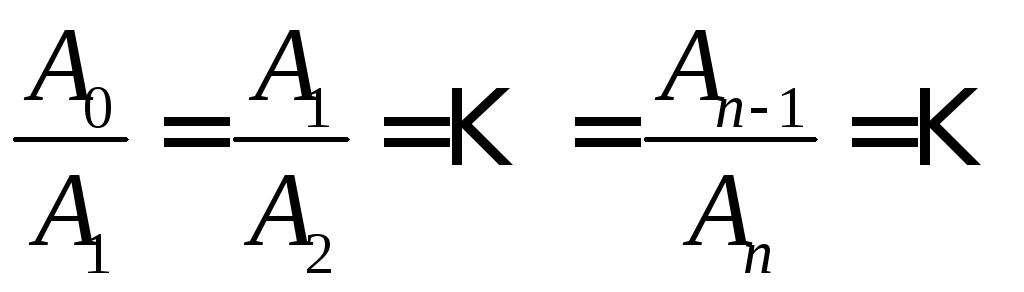
Из алгебры известно, что именно таким свойством обладает показательная функция, т.е. в общем виде можно записать соотношение пропорциональности
![]() .
.
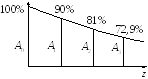
− Спадание амплитуды волны при распространении в среде с потерями
Здесь
![]() носит название постоянной затухания
волны. Величины
носит название постоянной затухания
волны. Величины![]() и
и![]() можно объединить, введя комплексную
постоянную распространения
можно объединить, введя комплексную
постоянную распространения![]() :
:
![]() .
.
Итак, вещественная часть
![]() определяет закон изменения фазы в
распространяющейся волне, в то время
как мнимая часть характеризует затухание.
определяет закон изменения фазы в
распространяющейся волне, в то время
как мнимая часть характеризует затухание.
