9. Четвертое уравнение Максвелла

Четвертое уравнение Максвелла в интегральной форме совпадает с законом Гаусса для магнитного поля, который можно сформулировать следующим образом. Поток вектора магнитной индукции через любую замкнутую поверхность равен нулю, т.е.

.

Это уравнение является четвертым уравнением Максвелла и называется также принципом непрерывности магнитного потока. В дифференциальной форме четвертое уравнение Максвелла получается, аналогично третьему, с помощью теоремы Остроградского-Гаусса:

,

тогда

,

а так как объем может быть любым, то это равенство может выполняться только при

.

33. −Линии вектора магнитной индукции

Физически смысл этого закона заключается в неразрывности магнитных силовых линий, что было установлено экспериментально. Из замкнутости силовых линий следует, что поток, «втекающий» в объем , в точности равен потоку, «вытекающему» из этого же объема. Иначе говоря, не существует линий вектора, которые только входят, или, наоборот, только выходят из поверхности: они всегда пронизывают ее.

4. Лекция 4. Обсуждение уравнение Максвелла и следствий из них. Сторонние силы Метод комплексных амплитуд, применение к уравнениям Максвелла. Энергетические соотношения

Выше мы рассмотрели систему уравнений Максвелла в комплексе. Эта система, как указывалось, описывает все возможные электромагнитные процессы. Решая эту систему уравнений, мы находим соотношения между векторами электромагнитного поля и связанными с ними токами и зарядами.

В любом процессе можно выделить особенности, позволяющие рассмотреть частные случаи системы уравнений Максвелла, упрощающие их решение. Ниже мы рассмотрим различные варианты таких случаев.

1. Обсуждение уравнений Максвелла

Вернемся к полной сводке уравнение Максвелла. Рассмотрение первых двух уравнений дает нам представление о строении электромагнитного поля.

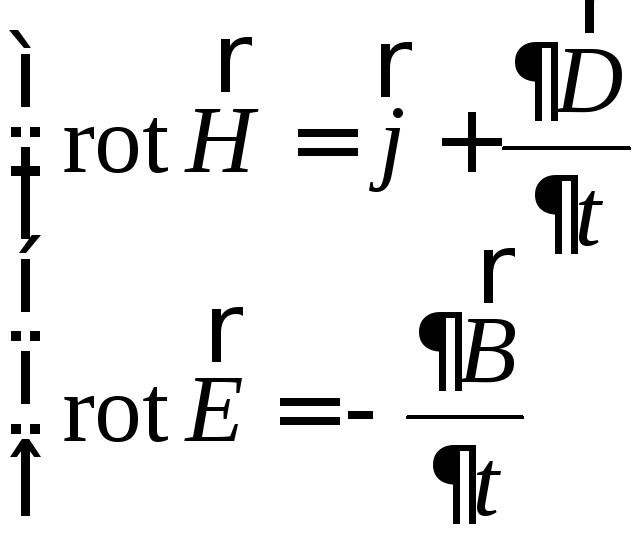
Из первого уравнения следует, что силовые линии магнитного поля охватывают линии полного тока, образуя с ними правовинтовую систему (). Аналогично, пространственный максимум магнитного потока охватывается семейством замкнутых электрических силовых линий.

34. − Строение электромагнитного поля

Первые два уравнения обладают симметрией в следующем смысле: по первому уравнению изменение во времени электрической индукции порождает вихревое магнитное поле, вектор напряженности которого изменяется в пространстве. По второму уравнению изменение во времени магнитной индукции порождает вихревое электрическое поле, изменяющееся в пространстве.

Из этого следует:

1. Электрическое поле может создаваться не только зарядом, но и переменным магнитным полем. Переменный магнитный поток неизбежно вызывает вихревое электрическое поле.

2. Магнитное поле возбуждается не только током проводимости, но и электрическим полем. Переменный по времени поток вектора электрической индукции 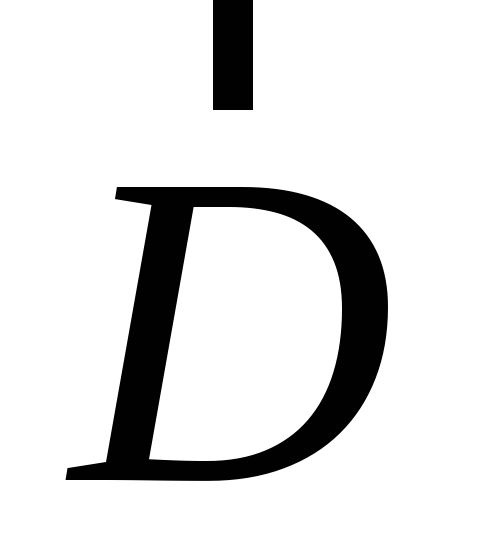неизбежно вызывает магнитное поле.

3. Электрическое и магнитное поля могут существовать, взаимно порождая друг друга. Например, если в некоторой области существует электрическое поле, то его изменение во времени (уменьшение или возрастание) приведет к появлению переменного магнитного поля. В свою очередь, изменяющееся магнитное поле вызовет вихревое электрическое поле. Происходит непрерывное взаимодействие между полями: одно поддерживает другое, и наоборот. Это определяет возможность существования электромагнитных волн в средах вдали от тел с токами проводимости.

35. −Возникновение электромагнитной волны

Физическая сущность такого процесса называется электромагнитной волной. Переменное электрическое поле в какой-то точке пространства вызывает, согласно первому уравнению, появление вокруг себя переменного магнитного поля. Это появившееся магнитное поле, в свою очередь, становясь причиной во втором уравнении, вызывает появление вокруг себя электрического поля и так далее. Схематически этот процесс показан на рисунке Рисунок 35 . Для получения полной картины поля во всем пространстве необходимо решить уравнения Максвелла.

Смысл третьего уравнения Максвелла прост, так как вполне исчерпывается понятиями дивергенции и потока вектора.

Линии вектора начинаются на положительных и заканчиваются на отрицательных зарядах. Если же в какой-либо области пространства заряда нет, то характер силовых линий векторадолжен соответствовать рисунку, т.е. количество линий «вошедших» в область, должно быть равно количеству «вышедших» и в этой области.

36. − Силовые линии вектора электрической индукции

Как следует из вывода третьего уравнения, его интегральная форма представляет собой теорему Гаусса:

.

Четвертое уравнение по форме отличается от третьего нулевой правой частью. В силу четвертого уравнения расхождение (дивергенция) вектора магнитной индукции везде равна нулю. Это означает, что магнитные силовые линии (линии вектора ) всегда непрерывны, т.е. либо замкнуты, либо идут из бесконечности в бесконечность. Характер картин магнитных силовых линий, таким образом, представлен на рисунке Рисунок 37 .

37. −Картина силовых линий магнитного поля

Непрерывность магнитных силовых линий указывает на отсутствие в природе фактора, который можно было бы называть «магнитным зарядом».