13. Векторы н и Dэлектромагнитного поля

Если ограничиться только рассмотрением процессов в вакууме, то для описания электромагнитного поля будет достаточно знания векторов и. Однако, как мы увидим далее, для описания поля в материальных средах (веществах) этих векторов недостаточно. Поэтому в рассмотрение вводятся два других вектора электромагнитного поля: вектор электрического смещения (или электрической индукции)и вектор напряженности магнитного поля. В вакууме они связаны с векторамииследующим образом:

,

где − размерная постоянная, найденная экспериментально и называемая электрической постоянной вакуума. Единица измерения вектора электрической индукции – Кл/м².

Вектор напряженности магнитного поля определяется по соотношению

,

где − размерная постоянная, называемая магнитной постоянной вакуума.

14. Сводка векторов и их единиц измерения

Подводя краткий итог, представим основные рассмотренные понятия в таблице.

Название величины	Обозначение	Единица измерения
Заряд		Кулон, Кл
Ток		Ампер, А
Объемная плотность заряда		Кулон на куб. метр, Кл/м3
Плотность тока		Ампер на кв. метр, А/м2
Напряженность электрического поля		Вольт на метр, В/м
Напряженность магнитного поля		Ампер на метр, А/м
Электрическая индукция		Кулон на кв. метр, Кл/м2
Магнитная индукция		Тесла
Электрическая постоянная		Фарад на метр, Ф/м
Магнитная постоянная		Генри на метр, Гн/м

3. Лекция 3. Основные законы электромагнетизма. Параметры сред. Уравнения Максвелла. В дифференциальной и интегральной форме

   1. Закон Гаусса

Этот закон получен экспериментально на основе закона Кулона и устанавливает связь между векторным полеми величиной порождающего его заряда. Он формулируется следующим образом. Рассмотрим некоторый объем, ограниченный замкнутой поверхностью. Если внутри объемазаключен суммарный заряд, то его величина, деленная на электрическую постоянную вакуума, численно совпадает с потоком векторного полячерез поверхность.

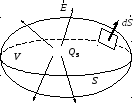
25. − Закон Гаусса

Математически закон Гаусса записывается как

.

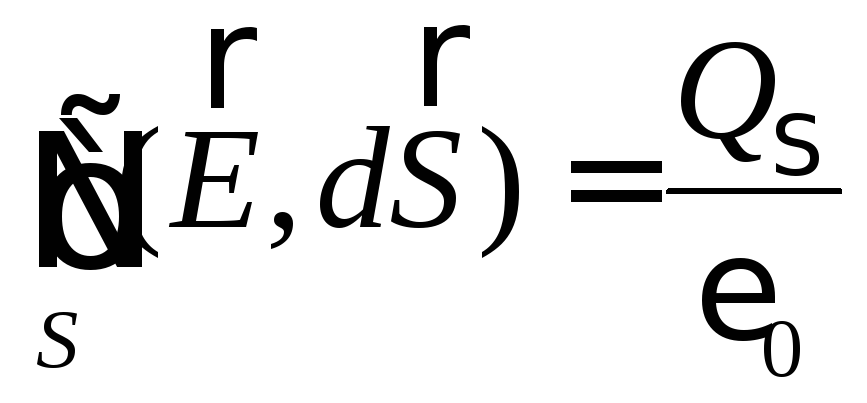Если рассматриваются точечные заряды, то величина может быть найдена алгебраическим суммированием. Если же заряд распределен непрерывно, то его суммарная величина определяется интегрированием объемной плотности заряда по объему:

.

2. Закон электромагнитной индукции (Фарадея)

Рассмотрим теперь ряд законов, связывающих между собой векторы электромагнитного поля, заряды и токи. Первый из них – закон электромагнитной индукции, носящий также имя закона Фарадея. Фарадей обнаружил, что на концах катушки, помещенной в переменное магнитное поле, возникает электродвижущая сила.

Введем сначала понятие разности потенциалов.

Разность потенциалов представляет собой отношение работы, затраченной на перемещение заряда , находящегося в электрическом поле, к величине этого заряда. Так как на заряд в поле действует сила Кулона, то при его перемещении из точкив другую точкуработа определится как

где − единичный вектор, направленный вдоль направления перемещения. При перемещении заряда по контуруиспользуется контурный интеграл.Единицей измерения разности потенциалов является вольт.

Кроме того, необходимо понятие магнитного потока: это поток вектора магнитной индукции через поверхность :

Рассмотрим теперь магнитное поле в пространстве. Поместим в это поле замкнутый контур , направление обхода которого при интегрировании – против часовой стрелки, если смотреть с конца вектора(рисунок Рисунок 26 ). Контуромограничена поверхность. Закон электромагнитной индукции гласит: изменение во времени магнитного потока через поверхностьвызывает в контуреэлектродвижущую силу, определяемую циркуляцией векторапо контуру. Это может быть записано следующим образом:

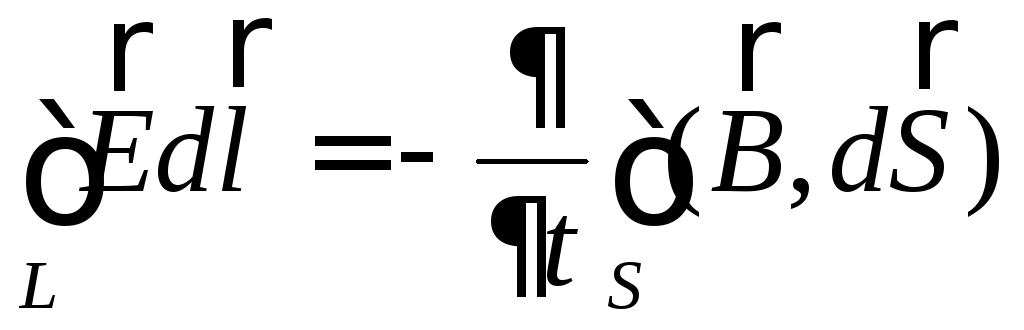
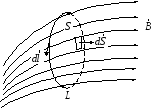
26. −К закону электромагнитной индукции

То есть, переменное магнитное поле приводит к возникновению напряжения. Чем быстрее меняется поле вокруг контура – тем выше напряжение.