4ПМ_Б_Комп_Модел_Власова / Индивидуальные задания лабораторные работы / Построение тренда

Лабораторная работа 4.

Тема: «Выявление тренда».

Решение задачи состоит из следующих двух этапов:

• проверка законов распределения,

• изучение динамики.

Рассмотрим первый этап, он состоит из следующих задач:

• нахождение математического ожидания, дисперсии и среднеквадратичного отклонения,

• исключение выбросов,

• нахождение размаха выборки,

• нахождение эмпирического распределения,

• проверка законов распределения.

Исследователь должен выбрать все пункты и вывести все результаты в одном отчёте. Отчёт лучше представить в форме таблицы и вывести основные графики.

1. Нахождение математического ожидания, дисперсии и среднеквадратического отклонения.

• - математическое ожидание – среднее арифметическое от всех значений

- значение, введённое пользователем, n – число этих значений,

• - дисперсия – сумма квадратов разностей между значениями и математическим ожиданием (средним арифметическим).

• (среднее квадратичное отклонение – корень из дисперсии)

В отчёте выводим значения:

«Математическое ожидание»

«Дисперсия»

«Среднее отклонение»

1. Исключение выбросов

Проверяется условие по :

Если , то - выброс и его следует исключить, т.е. убираем его из ряда значений. Выводим в отчете:

– выброшенные значения и номер периода (порядковый номер выброшенного значения).

– ряд новых значений, уже без выбросов.

2. Нахождение размаха выборки

По новой выборке (новому ряду, без выбросов) находим y максимальное и y минимальное. Затем строим размах выборки:

Выводим в отчёте значение числа H с подписью – «размах выборки».

3. Нахождение эмпирического распределения

Разбиваем выборку на k интервалов(k = 1 + 3,32 lg n) с шагом y= (шаг равен размах выборки разделить на k )

Строим таблицу (и выводим её в отчёте)

Номер, N	Интервал, i
1	[ymin, ymin+y) начиная с ymin прибавляем к y, строим интервалы.	в этой графе пишем число значений, попавших в данный интервал	Делим это число на число всех значений
2
…
k

4. Проверка законов распределения

Рассмотрим два закона распределения: Нормальный закон распределения и закон распределения Пуассона.

1) Нормальный закон распределения

По формуле находим частоту теоретического распределения для каждого интервала.

Проверяем гипотезы:

H₀ – «случайная величина распределена по нормальному закону распределения»

H₁ – «случайная величина не распределена по нормальному закону распределения»

Выбираем уровень значимости =0,05 , и вычисляем число степеней свободы  =k – 3 (3 – число фиксированных параметров в формуле).

Находим значение критерия по формуле .

Если полученное фактическое значение ² превышает табличное при том же уровне значимости и числу степеней свободы, то вероятность соответствия распределения нормальному закону меньше указанной,то гипотеза H_{0 (}случайная величина распределена по нормальному закону распределения) – противоречива, то есть принимается гипотеза H_{1 (}случайная величина не распределена по нормальному закону распределения).

Если табличное значение ² превышает полученное фактическое при том же уровне значимости и числу степеней свободы, то вероятность соответствия распределения нормальному закону меньше указанной, и гипотеза H_{0 (}случайная величина распределена по нормальному закону распределения) – не противоречива.

1) Закон распределения Пуассона

По формуле (частота теоретического распределения по нормальному закону) подсчитываем . Здесь:

• n – число экспериментальных данных,

• - среднее арифметическое наблюденных значений,

• x_i – значение i-ой случайной величины.

Проверяем гипотезы:

H₀ – «случайная величина распределена по закону распределения Пуассона»

H₁ – «случайная величина не распределена по закону распределения Пуассона»

Выбираем  =0,05 и находим значение критерия по формуле

Из таблицы для соответствующего значения уровня значимости  и числа степеней свободы  =k – 3 (3 – число фиксированных параметров в формуле) найдем величину вероятности P().

Если P()> , то гипотеза о том, что случайная величина распределена по нормальному закону распределения, не противоречива, то есть принимается гипотеза Н₀, в противном случае принимается гипотеза Н₁.

1. Изучение динамики

На этом этапе необходимо определить основные показатели, характеризующие тенденцию динамики:

• Средние показатели тенденции динамики

• Выявление типа тенденции динамики тренда

• Определение оптимального значения тренды

Все результаты выводятся в одном отчёте. Отчёт целесообразно оформить в виде таблиц и вывести соответствующие графики. Как и в первом случае все последующие пункты зависят от предыдущих.

1. Основные показатели, характеризующие тенденцию динамики:

Строится таблица:

Номер	Уровень ряда	Абсолютное изменение уровней ряда		…	…
		Цепное	Базисное

Столбцы:

1. Номер периодов или моментных рядов от 1 до n,

2. Уровни ряда - значения, введённые пользователем,

3. Абсолютное изменение уровней подпункты:

• Цепное

• Базисное

4. Ускорение абсолютного изменения:

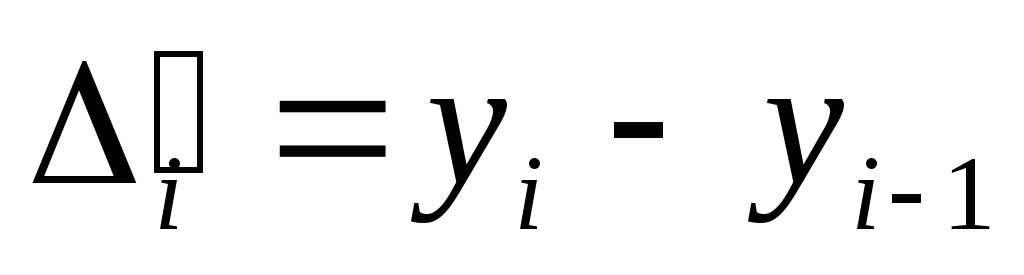
5. Темп роста в % :

• к предыдущему периоду

• к начальному периоду

6. Темп прироста:

• Цепной

• Базисный

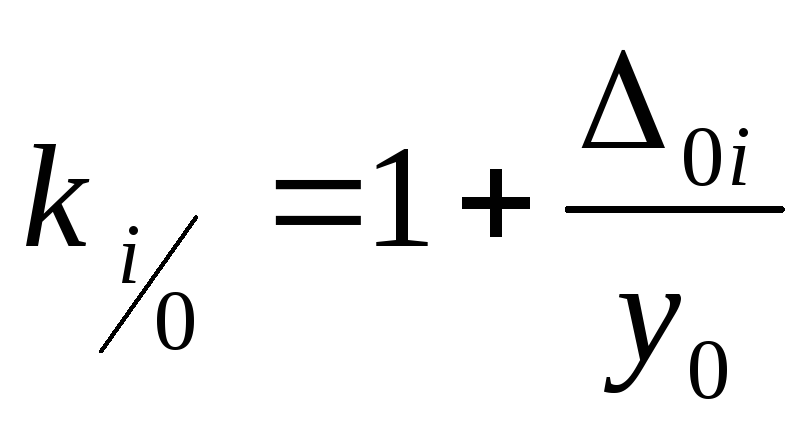
7. Абсолютное значение 1% прироста:

2. Средние показатели тенденции динамики

Строится таблица:

N	Уровень ряда	Средний уровень интервального ряда динамики	Средний абсолютный прирост	Средний темп изменения

Столбцы:

1. Номер периода

2. Уровень ряда

3. Средний уровень интервального ряда динамики:

, где n – число периодов

4. Средний абсолютный прирост:

5. Средний темп изменения:

3. Выявление типа тенденции динамики тренда

Выясняем тип динамики тренда графически. Для этого сравниваем исходный (заданный) график с возможными вариантами тренда:

1. линейная форма тренда: формула для рисования кривой: ,

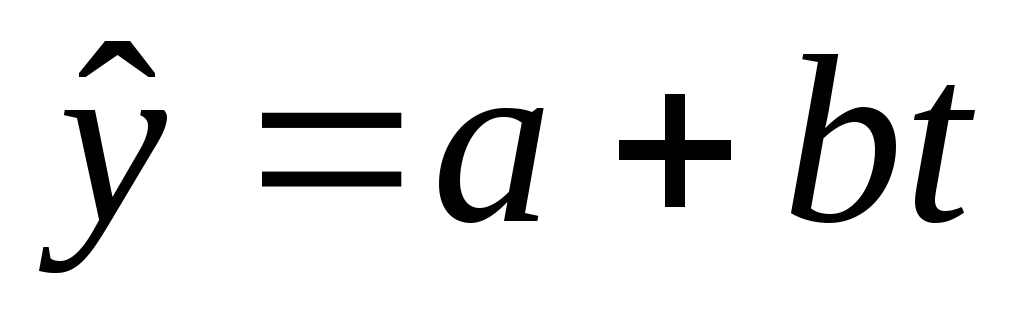где a – начальное условие (начальное значение ()), b- средний абсолютный прирост (был подсчитан выше)

2) Параболическая форма тренда: , где а – начальное условие (начальное значение ()), b- средний абсолютный прирост , с = ,

3. Экспоненциальная форма 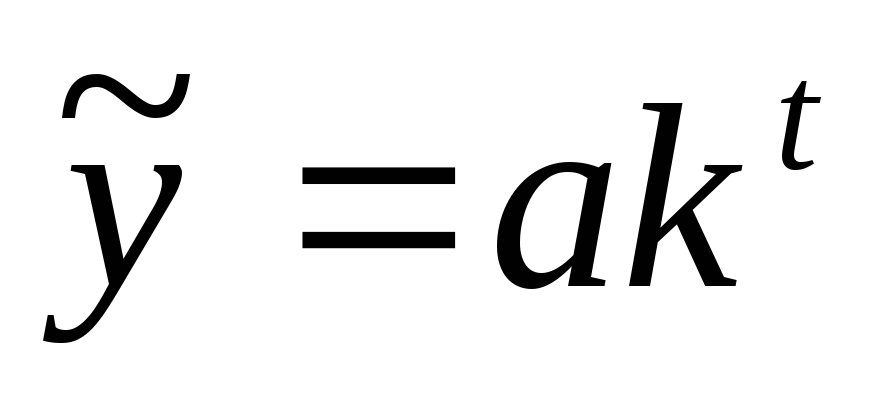, где k – средний темп изменения (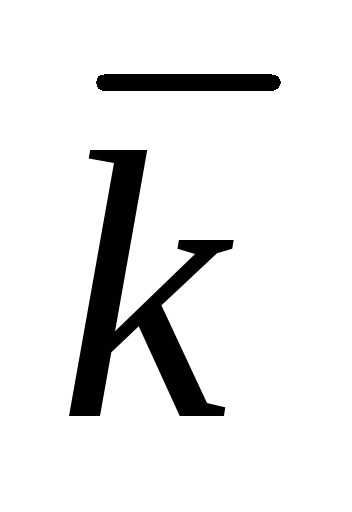) (был подсчитан выше),

4) Логарифмическая форма тренда ,

5. Степенная ,

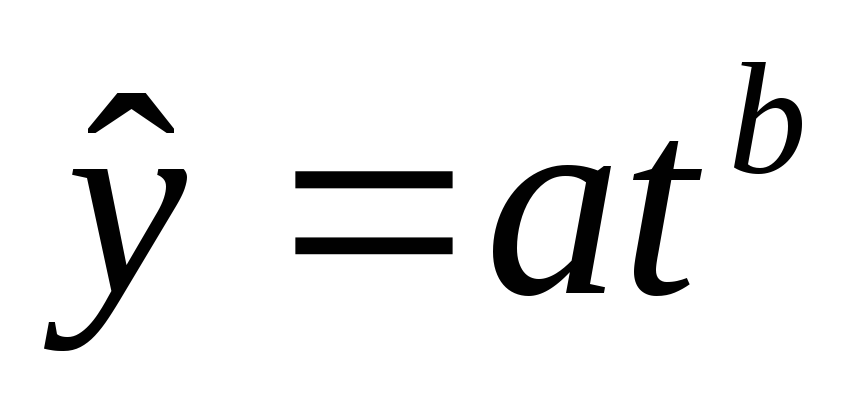6. Гиперболическая ,

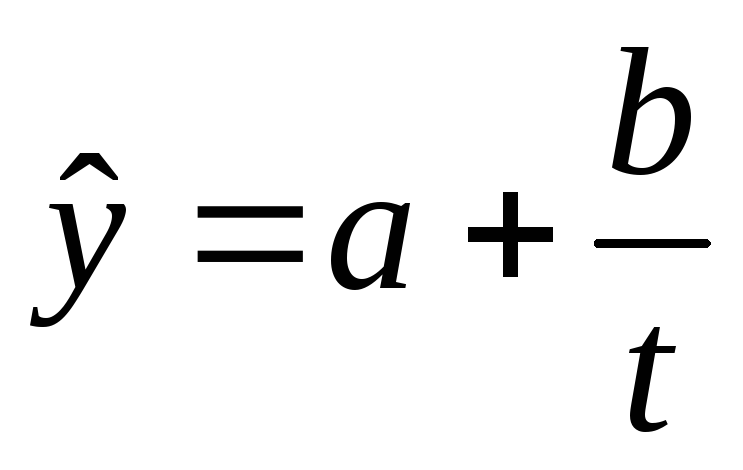7. Логистическая

4. Определение оптимального значения тренда

Если тренд не является ни 1), ни 2) ни 3) (линейным, параболическим или кспоненциальным), то просто строим график и пишем название типа тренда, который выбираем на основании графика, построенного по экспериментальным данным.

Если были подобраны пункты 1), 2) или 3), то определяем оптимальное значение тренда:

1. для линейного тренда подсчитываем новые значения по формуле:

, где , ,

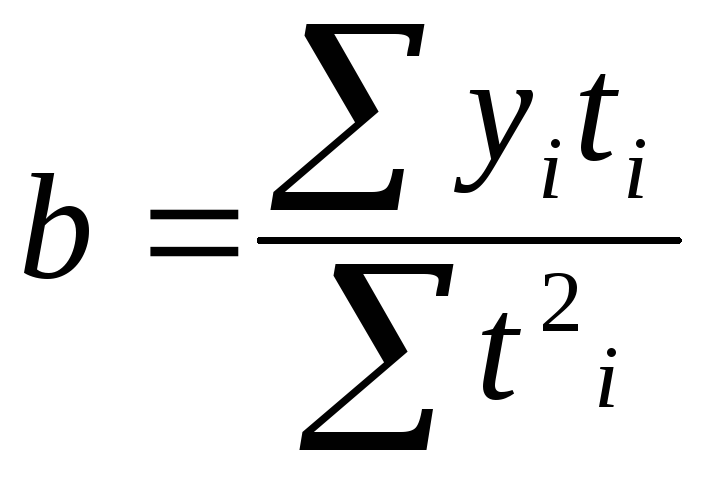здесь t принимает значение от до .

Значения выводим в таблице и строим график для новых значений y.

2. для параболы второго порядка подсчитываем новые значения по формуле: 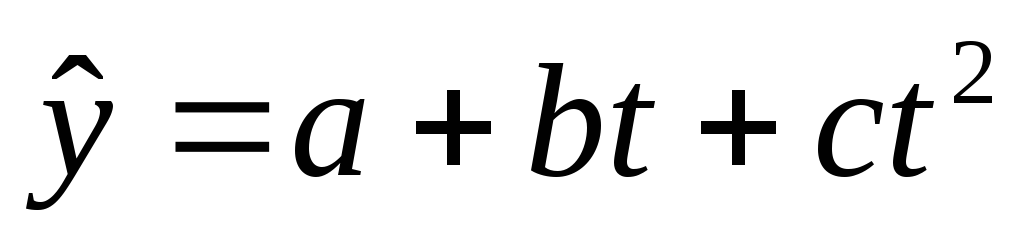, где надо найти значения a, b и c . Для этого решим систему уравнений:

,

где t принимает значение от до

результаты представим в виде таблицы, и построим график для новых значений y.

3. для экспоненциального вида тренда подсчитаем новые значения по формуле: ,

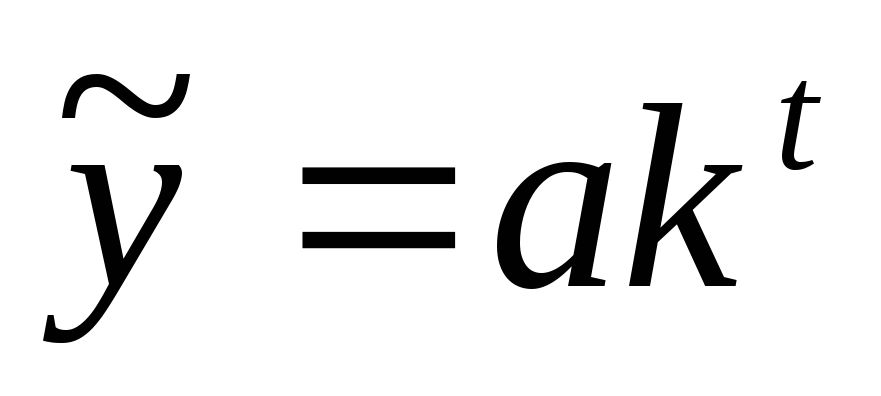здесь значения a и k аналогичны формуле для линейного тренда:

, где t принимает значение от до

Результаты выводим в виде таблицы, строим график для новых значений у.