
Вопрос 17. Резонанс напряжений
Рассмотрим вновь схему рис. 4.2. Для этой цепи комплексное значение входного сопротивления:
 (4.34)
(4.34)
Очевидно, всегда существует такое
значение частоты
 когда выполняется условие:
когда выполняется условие:
При этом
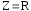 ,
т.е. входное сопротивление схемы будет
чисто активным, а ток схемы совпадает
по фазе с напряжением питания
,
т.е. входное сопротивление схемы будет
чисто активным, а ток схемы совпадает
по фазе с напряжением питания ,
соответственно=
0,cos= 1.
,
соответственно=
0,cos= 1.
Значение
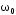 определяется формулой:
определяется формулой:
 ,
(4.35)
,
(4.35)
тогда

 ,
,
то есть индуктивное и ёмкостное сопротивления равны между собой:
 ,
,
где
 называют характеристическим или волновым
сопротивлением цепи.
называют характеристическим или волновым
сопротивлением цепи.
Добротностью резонансного контура называют отношение:
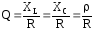 .
(4.36)
.
(4.36)
Обратное отношение называется затуханием контура
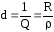 .
(4.37)
.
(4.37)
Распределение напряжений в схеме в режиме резонанса:
 ,
,
то есть напряжение на активном сопротивлении равно приложенному напряжению.
Напряжения на активных элементах при резонансе:
 .
.
Они
могут быть выше напряжения питания,
если
 XL=XCR, то естьQ1.
XL=XCR, то естьQ1.
Векторная диаграмма схемы рис. 4.2 в
режиме резонанса напряжений приведена
на рис. 4.16.
Хотя реактивная мощность, потребляемая схемой. равна нулю, запас реактивной энергии в схеме не равен нулю. В схеме происходит непрерывное перераспределение энергии магнитного и электрического полей, суммарное значение которой постоянно:
WL+WC= .
.
Для глубокого уяснения процессов.
происходящих в рассматриваемой схеме,
полезно построить графики зависимости
от частоты токов и напряжений схемы.
Если величина приложенного к схеме
напряжения не меняется с изменением
частоты, кривая тока (рис. 4.17) имеет
максимум при
 ,
что видно из соотношения:
,
что видно из соотношения:
 .
.

Форма кривой тока будет более островершинной при больших значениях добротности.
Значения
 и
и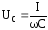 при резонансе равны между собой, но эти
значения не являются наибольшими.
ВеличинаUC
достигает максимума при0,
аUL
– при0. Фазовый
угол также изменяется в пределах от
+900 эл. до -900 эл. в соответствии
с соотношением
при резонансе равны между собой, но эти
значения не являются наибольшими.
ВеличинаUC
достигает максимума при0,
аUL
– при0. Фазовый
угол также изменяется в пределах от
+900 эл. до -900 эл. в соответствии
с соотношением
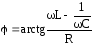 .
.
Кривая изменения () показывает, что при0 схема работает в ёмкостном режиме, а при0 - в индуктивном.
Вопрос 16. Резонанс токов
Рассмотрим вначале идеализированную схему рис. 4.9. Полная проводимость схемы:
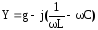 .
(4.38)
.
(4.38)
При некотором значении =0 :Y=gи схема ведёт себя как
чисто активная проводимость, при этом ,
откуда
,
откуда ,
что совпадает с (4.32). То есть для схемы
рис. 4.9 условие резонанса токов и условие
резонанса напряжений одинаковы.
,
что совпадает с (4.32). То есть для схемы
рис. 4.9 условие резонанса токов и условие
резонанса напряжений одинаковы.
Очевидно, что в режиме резонанса токов IL=IC, а общий ток схемыI= =Iа.
Характеристическая или волновая проводимость схемы:
 .
(4.39)
.
(4.39)
Добротность
схемы
 .
.
Затухание
схемы
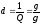 .
.
Векторная диаграмма схемы приведена на рис. 4.18.

Форма резонансных кривых при varприведена на рис. 4.19.

При 0 в схеме преобладает индуктивный ток, при0– ёмкостный.
Рассмотренная схема является идеализированной. В ней не учтено, что реальная катушка индуктивности всегда имеет некоторое активное сопротивление R1( сопротивление провода катушки и ряд других факторов), а реальный конденсатор за счёт несовершенства его изоляции также имеет активные потери, что на схеме замещения должно быть учтено активным сопротивлениемR2 . В связи с этим в реальных условиях явление резонанса токов следует рассматривать на примере схемы рис. 4.20.

Здесь условие резонанса токов – равенство реактивных проводимостей параллельных ветвей – запишется с учётом (4.15) в следующем виде:
bL=bC,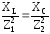 ,
,
или
 ,
,
откуда
 .
(4.40)
.
(4.40)
Отсюда видно, что в данном случае резонансная частота 0 зависит не только отLиC, но и от активных сопротивленийR1иR2 . В зависимости от соотношения этих сопротивлений иL/Cвозможны следующие частные случаи:
R1=R2 = 0, тогда
 ,
что соответствует ранее рассмотренному
случаю.
,
что соответствует ранее рассмотренному
случаю.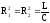 – формула 4.40 даёт неопределённость,
что соответствует режиму резонанса на
любой частоте.
– формула 4.40 даёт неопределённость,
что соответствует режиму резонанса на
любой частоте.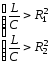 либо
либо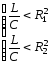 ,
,
то есть числитель и знаменатель второго корня (4.40) имеют одинаковый знак. При этом резонанс возможен при частоте, определяемой формулой 4.40.
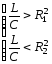 либо
либо ,
,
то есть числитель и знаменатель имеют разные знаки. В этом случае резонанс в схеме невозможен. Векторная диаграмма схемы приведена на рис. 4.21. Нетрудно заметить, что как и в предыдущем случае при резонансе вся схема имеет чисто активную проводимость:
 .
.

Вопрос № 10. Синусоидальный ток в R
