All lectures pdfs / Ур.мат.физ / Lecture_2 / 2010-08-29 / Лекция_2

По теореме о неявно заданных функциях векторное уравнение x = x(t; x0) может быть однозначно разрешено относительно x0 : x0 = x0(t; x) и система ©xi0(t; x); i = 1; nª может быть взята в качестве системы функционально независимых первых интегралов векторного уравнения (¤).

Общее решение уравнения (1).

u = F ©©(1)(t; x); :::; ©(n)(t; x)ª; F - произвольная функция (достаточно гладкая).

Свойство любого решения уравнения (1): вдоль характеристики решение u постоянно. Далее уравнение (1) можно еще переписать так:

dudt = 0, где dtd = L - полная производная от u вдоль характеристики.

Задача Коши для уравнения (1):

(

(2)

Lu = 0; ujt=t0 = '(x);

где '(x) - некоторая гладкая функция.

Формализм построения решения задачи Коши (2):

8

>>©(1)(t0; x) = ©(1);

<

а) >.

>

:©(n)(t0; x) = ©(n):

Из этой системы находим зависимость x = X(©(1); :::; ©(n)):

б) Тогда решение задачи Коши (2) записывается так:

u = '(X(©(1)(t; x); :::; ©(n)(t; x))):

Замечание. Уравнение (1) можно трактовать так: dudt = 0 - пол-

ная производная от u в силу системы (¤) равна 0. Это означает, что вдоль характеристики функция u постоянна.

Рассмотрим вместо уравнения (1) более общее уравнение:

(10) f0(t; x)ut + (f; ru) = 0:

Рассмотрим два предельных случая. 1-ый предельный случай.

Если f0 =6 0, то (10) перепишется в виде (1)

(100) ut + µ 1 f; ru¶ = 0; f0

характеристики которого определяются из соп. системы:

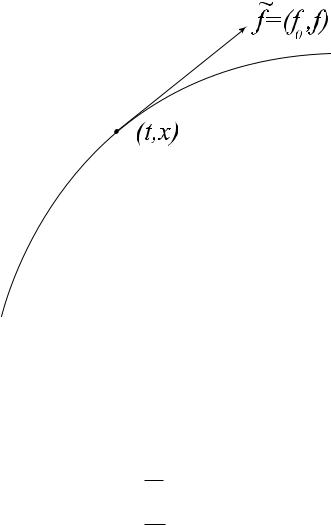
Заметим, что вектор f = (f0; f) = (f0; f1; :::; fn) определяет век-

Говорят, что этот вектор задает характеристическое направление в точке (t; x). Если мы решаем задачу Коши для уравнения (10) ((100)) с данными при t = t0 : ujt=t0 = '(x), то гиперплоскость t = t0 ни в одной точке не имеет хар. направления.

2-ой предельный случай.

Если f0(t; x) ´ 0, то (10) перепишется так:

(1000) (f(t; x); ru) = 0;

характеристики которого находятся из системы:

8

> dt = 0; < ds

> dx

: ds = f;

т.е. при t = const характеристики расположены в гиперплоскости t = const. Поскольку вдоль каждой такой характеристики u

постоянно, то следовательно задача Коши

(

(f; ru) = 0; ujt=t0 = '(x)

разрешима не при любой функции '(x). Промежуточный случай будет рассмотрен далее на примере.

До сих пор мы рассматривали данные Коши на гиперплоскости t = t0. Рассмотрим теперь так называемую обобщенную задачу

Коши, которая ставится так:

(

(3)f0ut + (f; ru) = 0;

uj° = '(t; x); (t; x) 2 °:

Здесь ° - гладкая гиперповерхность с уравнением

> 0

= 0

<0

Следовательно задача (3) перепишется так:

означает, что вектор fe не лежит в касательной гиперплоскости к гиперповерхности ° (иными словами, ни в одной точке поверхность ° не имеет характеристического направления).

Примеры:

1) xut ¡ (t + 1)ux = 0; x 2 R1; уравнение характеристик: dxdt = ¡t +x 1,

т.е. общее решение: u = F(x2 + (t + 1)2):

Найдем решение задачи Коши при t > 0 с начальным условием:

ujt=0 = x:

Однако простые рассуждения показывают, что начальное условие можно задавать либо при x < 0, либо при x > 0 (на всей оси t = 0 начальное условие задавать нельзя!). Если начальное условие

задается при x < 0, то решение имеет вид:

p

u = ¡ x2 + (t + 1)2 ¡ 1; t > 0:

Причина того, почему начальное условие нельзя задавать при

t

x

-1

всех x, заключается в том, что в точке (0; 0) линия t = 0 имеет характеристическое направление.

2)ut + ux = 0; u = F(x ¡ t); ª = x ¡ t; f0ªt + f1ªx = 0:

2.Квазилинейные уравнения с частными производны-

ми.

(4) Luk = gk(t; x; u); k = 1; m;

@

L = @t + (f; r); f = (f1; :::; fn);

fk = fk(t; x; u); k = 1; n;; u = (u1; :::; um).

Система (4) называется квазилинейной. Если f = f(t; x), то система называется почти линейной.

а) Нахождение общего решения.

8 > dx

(5) < dt

> du

:

dt

(соп. сист. об. диф. уравнений).

Интегральные кривые системы dxdt = f(t; x; u) называются харак-

теристиками системы (4). Но в отличии от лин. уравнения (1), в квазилинейном случае нельзя найти характеристики, не зная

решения u = u(t; x). Каждое уравнение системы dudt = g(t; x; u)

называется соотношением на характеристике. Пусть f©(i)(t; x; u); i = 1; n + mg - какая-либо функционально независимая система первых интегралов системы (5). Тогда общее решение системы (4) дается в следующем виде:

т.е. функции uk; k = 1; m определяются неявно.

б) Решение задачи Коши

(

(6)

Lu = g;

ujt=t0 = '(x) = ('1(x); :::; 'm(x));

u = U(©(1); :::):

Тогда решение задачи Коши (6) дается в виде:

U(©(1)(t; x; u); :::) = '(X(©(1)(t; x; u); :::));

т.е. определяется в неявном виде.

Пример.

8 ut + uux = 0;

> dx

с.с.об.ур. < dt = u ! x ¡ ut = const; > du

: dt = 0 ! u = const:

(©(1) = x ¡ ut;

©(2) = u;

F(x ¡ ut; u) = 0 - общее решение. Задача Коши:

(

ut + uux = 0; ujt=0 = '(x)

имеет решение:

(8) u = '(x ¡ ut):

До сих пор, при построении решений того или иного уравнения, мы неявно предполагали, что строим гладкие решения, т.е. решения непрерывно дифференцируемые до некоторого порядка.

Так задача Коши: ut + ux = 0; ujt=0 = '(x) имеет гладкое решение при всех t > 0; x 2 R1, если функция '(x) непрерывно