Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный исследовательский университет «МИЭТ»

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Diss / 1

.pdf

Скачиваний:

Добавлен:

27.03.2016

Размер:

1.14 Mб

Скачать

☆

<<< < Предыдущая 12 / 32 3 > Следующая >>>

				)			Ù			)	δ							)		Ù = Z*Ø Z ,			(36)
				p(R)= (π δ !(δ +1)! )−1			Ù		δ +2	R			exp{−tr(Ù R)},							Ù = Z*Ø Z ,			(36)
а первые три СФ (1) связаны с элементами														2 ×2				матрицы		Q (28) равенствами
				)	)	)		)		/ (N			)			2	),	)	) )		)	2	(37)
				)	)	)		)					)			2		)	) )		)	2
				S1	=1/(N q22 ) ,	S2		= q11					q12					S3 = q11q22 /			q12
(для простоты обозначений мы пока опускаем аргумент α																				этих СФ).
			Тем самым решаемая задача сводится к решению двух подзадач:
a)		отысканию плотности				2 ×2		матрицы						Q (28) по плотности (36) матрицы									R (29)
b)		вычислению плотностей распределения функций (37) элементов Q .
			Для решения первой из них достаточно учесть, что якобиан преобразования (29) равен
	)		2k	и, следовательно, при k				= 2
	)		2k
	Q
				p(Q)= (πδ !(δ +1)!)−1 Ù								Q						exp{−tr(Ù Q−1 )}.					(38)
					)					δ +2			)		−(δ +4)					)



			Вторая		задача существенно					сложнее.								Она	требует достаточно				нетривиальных

преобразований, вычислений их якобианов и интегралов, содержащих специальные функции, которые, впрочем, сводятся к справочным [31].

Опуская подробности, приведем «финальную» совместную плотность величин,

полностью определяющих искомые случайные СФ S2

и S3

(37):

(ν

,ν

)= d

exp −

Nν2

exp −

Nν2

−

Nν2

1+C ν

C ν

(1+C ν

)

δ +1

3 3

(39а)

d23 = (ä! C3ν32 )−1 N ä+2 ν2ä+1(C3 / (1+C3ν3 ))ä+2 .

Здесь

Ln (•)- полином Лагерра степени

n [31],

ν2 = S2 / S2 ,

ν3

= C3 / C3 ,

C3 = S3 −1 -

(39б)

нормированные к «истинным» значениям соответствующих СФ.

Интегрируя (39а) от 0 до ∞ по ν2 (ν3 ), получим плотности pν (x) нормированных СФ ν =ν3 (ν =ν2 ). Интеграл по ν2 записывается при этом в виде

pν (x)= pν3 (x)= Cδ +1 (δ +1)δ∑+1

xδ

δ +2+n

n=0 C

(1+(1+C)x)

(δ +1+n)!

(40)

, C = C

= C

(α)= S

(α)−1.

(n!)2 (δ +1−n)!

Получить явное выражение для интеграла

∞
pν (x)= pν2 (x)= ∫pc (x, y)dy	(41)
0
не удается, поэтому плотность pν2 (x) методов ЛП определяется	методами численного
интегрирования.

Проводимый в п.5 анализ разрешающей способности методов (1) по статистическим критериям разрешения-обнаружения базируется на точных формулах (34), (40), (41) и

эмпирических законах распределения в «точке» СФ S4 (α) и S5 (α) методов БЛ и ТШ,

полученных на моделях, тестированных по точным формулам.

5. Сравнительный анализ разрешающей способности по статистическим критериям разрешения-обнаружения

А. Будем		полагать, что решение	об обнаружении		сигнала		с направления		поиска
α (αн,αк )	принимается по результатам сравнения с порогом					v(α)	случайных СФ			S (α)
методов (1). Их разрешающая способность в этом случае определяется ВЛТ F								и ВПО	D :
∞		∞	∞		∞
F = ∫pS)	(x, S0 )dx = ∫pv (x, S0 )dx ,		D = ∫pS)	(x, SC )dx =	∫pv (x, SC )dx1 ,			(42)
v(α)		x0	v(α)		x0 /(SC / S0 )
где S0 = S0 (α)		и SC = SC (α)- значения истинных СФ			S(α)	в точке анализа			α	при
отсутствии и наличии источника в направлении				α , x0 = v(α)/ S0 (α)-			скаляр,	определяющий
превышение порогового уровня
		v(α)= x0 S0 (α)						(43)
над значением S0 (α), необходимое для обеспечения заданной ВЛТ							F . Вторые равенства в

(42) являются прямым следствием (33).

Нетрудно показать, что входящее в нижний предел второго интеграла в (42) отношение

SC / S0 = SC (α)/ S0 (α) для методов (1) одинаково и в	направлениях	α = βl ( l 1, n )
расположения источников равно (см. (17), (21))
SC / S0 = SC (βl )/ S0 (βl )=1+ µl , µl = ql kэ ,	l 1, n ,	(44)

т.е. определяется тем же ООСП µl , что и при оптимальной обработке в условиях полной априорной определенности (п.3).

Б. Начнем с анализа разрешающей способности		метода Кейпона. Как следует из
сравнения (34) с (15), для этого метода, в соответствии с (42),
F = fδ (Nx0 ),	D = fδ (Nx0 /(1+ µl )),	l 1, n ,	(45)

где fδ (x) - функция «выживания» распределения Эрланга с единичным параметром масштаба, но, в отличие от (19), с параметром формы δ +1 .

В сочетании с (20) это означает, что метод Кейпона в условиях (6), (3) теоретически обеспечивает в точности те же статистические характеристики разрешения-обнаружения, что и

оптимальная обработка (13)

K -мерной выборки

Y ={Y

, если объем

обучающей

i=1

выборки в МП оценке (27) удовлетворяет условию

δ = K −1 = N − M , то есть при

N = K +ε ,

ε = M −1.

(46)

Значение ε

определяет «плату» за априорное незнание КМ Ф (4), которая требуется при

использовании метода Кейпона на основе МП оценок (6), (7), (27). В частности, на

следует

увеличить значения

на рис.1а, чтобы определить статистические характеристики этого

метода в ЛЭАР при

n = 2 и α = βl (l 1, n) .

В. Соответствующая «плата» других методов (1) может быть существенно выше. Мы

проиллюстрируем это вначале на примере МАК с СФ

C(α)= S(α)−1

с плотностью (40) и

истинными значениями

C(α)= C0 при α ≠ βl

и C(α)= C1

при α = βl

( l 1, n ).

Можно

показать,

что в

этом случае пороговая

константа x0

(43)

является

корнем

уравнения

F = (C0 / (1+C0 ))δ +1(δ +1) δ∑+1an In (x0 ,C0 )/ C0n ,

(47)

n=0

а ВПО сигнала источника, действующего с направления α = βl ( l 1, n ), равна

D = (C1 /(1+C1 ))δ +1(δ +1)δ∑+1an In (x0 /(1+ µl ),C1 ), C1 = C0 /(1+ µl ),

n=0

где через

In (x,c) обозначен интеграл [31]

z(x,c)

(x,c)=

∫

tn (1

−t)δ dt

= zn

+1(x,c)

∑

+ k ),

(−1)k

zk (x,c)/(n +1

k =0

z(x,c)= (1+(1+c)x)−1,

а через

- число сочетаний из n

по

m .

(48)

(49)

Рассмотрим вначале ситуацию выборки «малого» эффективного объема δ , когда

(δ +1)(δ +2)< C0 , δ = N-M . (50)

Как показывает анализ, в этом случае определяющий вклад в суммы в (47), (48) вносят только первые слагаемые, так что

F ≈ (C0 /(1+C0 ))δ +1(δ +1)/(1+(1+C0 )x0 ), D ≈ ((1+C0 )(1+ µl )/(1+C0 (1+ µl )))δ +1 F .					(51)
Из первого равенства следует, что в условиях (50), когда δ << C0 ,
	x ≈ F −1(δ +1)/(1+C		0	).	(52)
	0		0
Это значение x	для представляющих основной интерес вероятностей F <10−3					может
0
оказаться значительно больше, чем значение		x0 в (45), требующееся в методе Кейпона, что
свидетельствует о существенно более «тяжелых хвостах» распределения (40), чем (34).
Из второго равенства в (51) видно, что при малых значениях ООСП µl <1					D ≈ F , что
вполне естественно. Однако в условиях (50) даже при сколь угодно больших						µl → ∞
вероятность правильного обнаружения
	D ≈ (1+1/ C0 )δ +1 F ≈ (1+(δ +1)/ C0 ) F ≤ (1+1/(δ + 2)) F ,				(53)
т.е. не более чем в	1.5 раза превосходят вероятность ложной тревоги F .

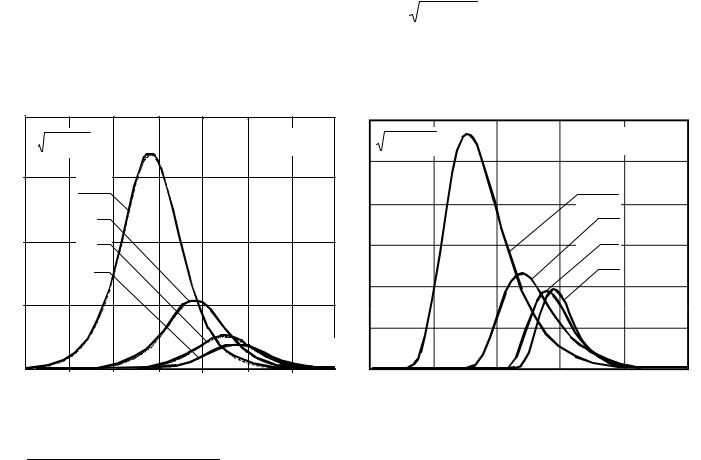
Формальное объяснение этому парадоксальному на первый взгляд эффекту можно дать,

анализируя трансформацию плотности (40) в условиях (50) при изменении ООСП µ = µl . На

рис.2а приведено семейство зависимостей g(x,C )=	p (x,C ),*)		C = C		0	(1+ µ)	для набора
1	ν	1	1		0
значений µ = 0, 1, 9, 99 ( C1 = C0 , 2 C0 , 10 C0 , 100 C0 ) при		C0 =15		и δ = 2 , когда условия
«малой выборки» (50) выполняются.

20											pν (x,C1 )
p	(x,C )					S0=15, δ= 2					pν (x,C1 )			S0=15 , δ = 100
ν		1
15									2.5
15		µ= 99												µ = 99
		µ= 99							2					µ = 99
			9						2						9
			9												9
10			1						1.5						1
			0						1						0
									1
5
									0.5
0								x	0						x
0															x

10-6	10-5		10-4	10-3	10-2	10-1	100	101		10-3		10-2	10-1	100	101	102
				а)					Рис.2					б)
									Рис.2
	*)	Использование корня из				p	(x,C )	продиктовано только стремлением к наглядности изображения,
						ν	1
которое		в	противном		случае	оказывается		неудобным			для	одновременного		наблюдения	существенно
“разновеликих” кривых. С этой же целью по оси									x	использован логарифмический масштаб,					позволяющий
наблюдать функции				pν	(x,C1 ), существенно различающиеся по ширине при различных значениях										C1 .
									14

Как хорошо видно, по мере роста µ плотность pν (x,C1 ) смещается в область все меньших значений x , в связи с чем вероятность получения значений ν ≥1 уменьшается. В

силу (33а), (39б), (40) это означает, что вероятность получения значений случайных СФ C3 (α)

( S3 (α)), близких к их истинным значениям C3 (α) ( S3 (α)), тем меньше, чем эти истинные

значения	больше. При	этом из-за	указанного «смещения влево» площадь под кривой
pν (x,C1 )	правее точки	x = x0 /(1+ µ), определяющая D (см. (42), (44)), остается практически
такой же, как площадь под кривой			pν (x,C0 ) правее точки x = x0 , определяющая F . В этом

состоит принципиальное отличие МАК от метода МД Кейпона, плотность (34) нормированной

СФ (33а) которого от абсолютного уровня			истинной СФ S(α) не зависит (последнее
обстоятельство было отмечено еще в [22, 23]).
По мере роста объема выборки		δ	(нарушения	условий (50)) «смещение влево»
плотностей	pν (x, C1 ) (40) с ростом	µ уменьшается,		что наглядно видно из рис.2б, где
δ =100 . В	этих условиях рост µ	сопровождается		ростом ВПО D , однако весьма

медленным, причем для каждого δ существует граничное значение	µ = µгр , превышение
которого уже практически не увеличивает значение D = Dгр . Они связаны неравенством
(δ +1)(δ + 2)< C1 = C0 (1 + µ),	(54)

при выполнении которого основной вклад в сумму (48) вносит первое слагаемое, а вкладом остальных можно пренебречь. В этом случае

D = Dгр ≤1−(C0 x0 /(1+C0 x0 ))δ +1 .

(55)

В частности, в условиях примера рис.2б при F =10−4

( x =100 ) значение

гр

≤ 0.06

при любых µ → ∞.

В связи с этим требования

к объему выборки для МАК

могут быть существенно выше,

чем для метода МД. Наглядное

представление

них

дают

F=10-4 , S0 = 15

характеристики

обнаружения

МАК, показанные на рис.3.

Сравнивая

их с

аналогичными

кривыми рис.1а при

δ = K −1,

нетрудно

убедиться,

что в

Рис.3

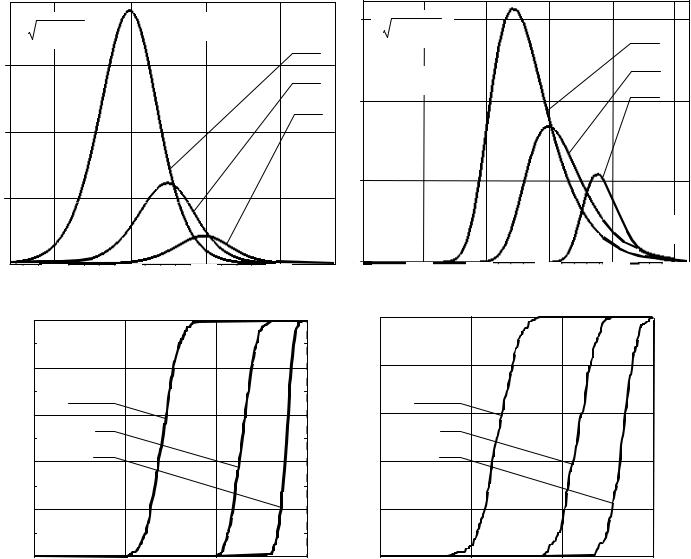
приведенных примерах характеристики, обеспечиваемые	методом Кейпона	уже при
δ = 0 , 4 ,19 , обеспечиваются МАК при δ > 200 , 400 , 1000	соответственно.

Г. На рис.4а,б показаны аналогичные рис.2а,б семейства плотностей метода ЛП, рассчитанные по (39), (41), а на рис.5а,б – полученные на математической модели эмпирические функции распределения нормированных (33а) СФ (1) методов БЛ и ТШ в условиях рис.2-4. Видно, что эффект «смещения влево» с ростом µ в той или иной мере присущ плотностям (функциям) распределения нормированных СФ всех этих методов. Поэтому требования к объему выборки δ для них, как и для МАК, оказывается существенно выше, чем для метода МД. Физические причины этих различий обсуждаются в п.7.

	(x,C )						3
p	(x,C )			S 0=15 ,	δ= 2		pν (x,C )						µ=99
ν		1				µ=99		1					µ=99
						µ=99							9
30						9	S 0=15 , δ		= 100				9
						9	S 0=15 , δ		= 100				0
						0	2						0
							2

20
							1
10
						x							x
						x	0
							0
10-6		10-4		10-2		100	10-3		10-2		10-1	100	101
			а)			0				б)		0
			а)			Рис.4				б)
						Рис.4
1	fν) (x )						1	(x )
	fν) (x )						fν)	(x )
0.8							0.8
		µ= 99						µ= 99
0.6		9					0.6		9
		9							9
0.4		0					0.4		0
0.4							0.4
		δ=50						δ=50
0.2							0.2
0						x	0						x
0							0
10-3		10-2	а)	10-1		100	10-3		10-2	б)	10-1		100
							Рис.5

Д. Установленные достоинства метода МД Кейпона по сравнению с другими методами (1) могли бы стать решающим доводом при выборе метода пеленгации в реальных условиях априорной неопределенности, если бы в этих условиях могла быть реализована практически

сама процедура обработки, предусматривающая сравнение случайных СФ (1) с порогом v(α)

во всех точках анализа α (αн,αк ). Этот порог, как следует из (43), определяется значением

истинной	СФ	S0 = S0 (α)	соответствующего метода, т.е. ее			значением при	отсутствии
источника	в	направлении	анализа	α .	Сравнение только с	таким порогом	обеспечит
«рекордные» (с минимальной «платой»				ε	(46)) статистические характеристики обнаружения
метода Кейпона при наличии источника в направлении анализа α .
Но значение S0 определяется КМ					Ф0 (12), которая априори неизвестна и вместо

которой реально должна использоваться та или иная (желательно - МП) ее оценка. Но, в

отличие от оценки (6) КМ Ф (4),				(9)	в целом, получить оценку	Ф0	КМ Ф0	для всех
α (αн,αк ), в том числе и при			α = βl	( l 1,n ), располагая только неклассифицированной при
α = β	l	обучающей выборкой	Y =	{Y	} N , исключительно сложно или даже невозможно.
	l			l	l=1
Именно		этим можно объяснить		широкое распространение		на	практике	других

(нестатистических) процедур и критериев разрешения, в частности, критерия Рэлея, не связанных с пороговой обработкой СФ S (α) во всех точках α интервала анализа. Ниже проводится статистический анализ разрешающей способности методов (1) по (нестатистическому) критерию Рэлея.

6. Статистический анализ разрешающей способности по критерию Рэлея

А. Процедуры пеленгации (анализа пространственного спектра) источников излучений методами (1) обычно предполагают формирование в точках α из выбранного сектора (αн,αк )

соответствующих СФ S (α) и последующий поиск их локальных максимумов. Число

максимумов далее отождествляется с числом n источников в этом секторе, а их координаты

αl и значения	S (αl )	( l 1, n ) – с направлениями и относительными интенсивностями
источников [1, 5,	6, 14,	25]. Разрешающая способность по критерию Рэлея определяется в

тестовой ситуации двух ( n = 2 ) равномощных ( q1 = q2 = q ) источников, которые считаются

разрешенными, если «глубина провала» между максимумами S (αl ),			l =1,2 , характеризуемая
параметром
γ) = S(αl )/ S (αср ),	l 1,2 ,	αср = (α1 +α2 )/ 2 ,	(56)
превышает априори выбранный порог	γ0 (обычно	γ0 = (1−3) дБ) [1, 14, 25].

Целью последующего анализа является сравнение разрешающей способности методов (1) на основе МП оценок (27), (6), (3) по критерию (56).

Б. Отметим прежде всего, что (вынужденный) переход от статистически оптимальных процедур и критериев к нестатистическим неизбежно порождает дополнительные энергетические затраты на разрешение. Эти затраты различны для методов (1). Они

минимальны в гипотетических условиях обучающих выборок бесконечного объема

N → ∞ ,

когда случайные СФ

S(α)

можно считать совпадающими с истинными СФ

S(α) (в силу

асимптотической несмещенности и состоятельности МП оценок (27), (6), (3)).

100

Как

показано

[16-19], в

этих

условиях

q, дБ

«лучшим»

из

методов

(1)

является

МАК,

«худшим»

МД.

–

метод

Асимптотическое (при

N → ∞ )

различие

между ними

количественно

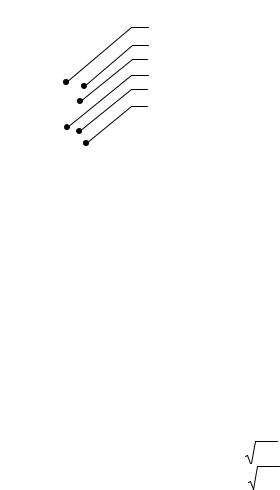
иллюстрируется рис.6, где показаны значения

ООСШ

(23) каждого

из

двух

равномощных

источников с угловым расстоянием ∆ (25) между

ними, необходимое для их разрешение в ЛЭАР.

∆

Кривые 1, 2, 3 здесь относятся к методу МД,

0.01

0.1

кривые 4, 5, 6 – к МАК при

γ =1

(кривые 1, 4) и

Рис.6

γ = 2 (кривые 2, 5). Кривые 3, 6 задают граничные

значения

q = qгр , при которых

точке

α =αср

(56) равны

нулю

вторые

производные

d 2S(α)/ dα2

соответствующих

истинных

СФ S(α)

[25].

При

q ≤ qгр

эти СФ имеют

единственный максимум в точке α =αср

и, следовательно, по критерию (56)

источники не

разрешаются. Они «начинают разрешаться» при [16-19, 25]

≈1.17 /

qгр

дляметода МД,

∆гр

(57)

∆ ≥

≈ 0.95/ 3 qгр

для МАК.

∆гр

Значения

qгр для остальных методов (1) несколько выше, чем

qгр

для МАК.

Из сравнения (57) с (26) видно, что при использовании критерия (56) дополнительные

энергетические

затраты тем

выше,

чем меньше расстояние

∆

между

источниками.

частности, при малых

∆ ≤ 0.1

они могут составить 10 −20 и более дБ.

В реальной ситуации конечных

N эти затраты еще больше из-за случайности параметра

разрешения

(56). Они зависят от его статистических свойств, существенно различающихся

для методов (1). Об этом свидетельствуют точные и экспериментальные результаты, обсуждаемые ниже.

В. Для метода МД плотность pν) (x) нормированного случайного параметра

ν) =γ) (α1,α2 )/ γ (α1,α2 ),

γ) (α1,α2 )= S(α1 )/ S(α2 ),

γ (α1,α2 )= S(α1 )/ S(α2 )

(58)

при произвольных

α1 ≠α2 и

δ ≥ 0 равна [15]

Г(2δ + 4)

δ +

xδ +1 (1+ x)

pν) (x)=

(1−

)

δ = N − M ≥ 0 .

(59)

(Г(δ + 2))2

((1+ x)2 −4

2 x)δ +2.5

Здесь через

η обозначен «обобщенный» коэффициент пространственной корреляции

излучений из направлений α1

α2 :

η = X*(α1 )Ø X(α2 ) (S1(α1 ) S1(α2 ))12 ,

S1(αi )= (X* (αi )Ø X(αi ))−1,

i =1,2 ,

(60)*)

совпадающий с (24) при Ф = Ø = IM

и векторе X(α)

вида (2).

При δ >>1

для среднего

)

и дисперсии

параметра

(58)

справедливы

σν)

приближенные равенства

)/ δ ,

2(1−

)/ δ .

)

≈

(61)

ν ≈1+ (1−

σν)

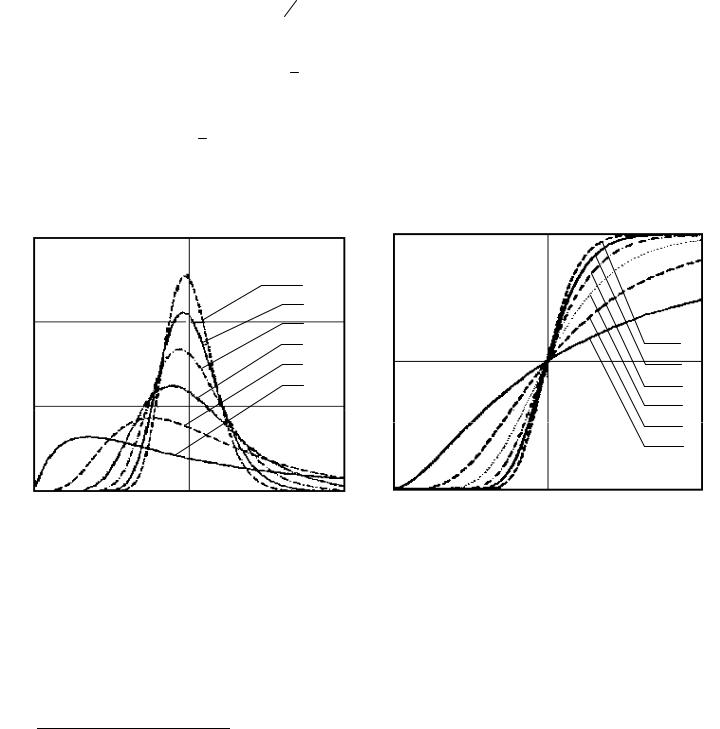
Пример плотностей (59) при

= 0.2

и различных значениях δ

приведен на рис.7а.

P(γ ≥γ0 )

pν) (x)

δ = 75

0.5

= 0.2

γ /γ0

а)

Рис.7

б)

Из анализа (59) следует важное свойство метода МД. Оно заключается в том, что при

любых объемах выборки δ ≥ 0

и значениях α1 ≠α2

случайный параметр

γ (α1,α2 )

будет не

ниже своего истинного значения

γ (α1,α2 )

(58) с фиксированной вероятностью

P = 0.5 . Это

утверждение является следствием справедливого для (59) равенства

pν) (x)= x−2 pν) (x−1 ),

(62)

*) Вид плотности (59) остается неизменным и при использовании МП оценок персимметричных КМ в центрально-симметричных АР, но в этом случае δ = N −(M +1)/ 2 [16-19].

означающего совпадение плотности (59)		положительной случайной величины		ν > 0 (58) и
обратной ей χ =1/ν . Оно означает также, что при любых α1 ≠α2 медианой плотности (59)
является точка x = x0 =1, то есть
	1	∞
	∫pν) (x)dx = ∫pν)		(x)dx =1/ 2 .	(63)
	0	1
Действительно, по условию нормировки
∞	x		∞
∫pν)	(x)dx = ∫0	pν) (x)dx + ∫pν) (x)dx =1.
0	0		x0
Но первое слагаемое этой суммы в силу (61) равно
x0			∞
∫1/ x2 pν)		(1/ x)dx = ∫pν) (x)dx
	0		1/ x0
и, следовательно,
	∞	∞
	∫ pν) (x)dx + ∫ pν) (x)dx =1,
	1/ x0	x0
откуда сразу следует равенство (63). В сочетании с (58) оно означает, что в методе МД
P(ν ≥1)= P(γ ≥ γ0 = γ )= 0.5			при любых δ ≥ 0 .	(64)
Последнее соотношение является математической формулировкой описанного свойства

метода МД. Оно иллюстрируется показанным на рис.7б семейством функций распределения

				γ / γ 0	∞
			fν (γ / γ0 )=	∫pν) (x)dx = ∫ pν) (x)dx = P(γ) ≥γ0 )					(65)
				0	γ / γ 0
для плотностей p)			(x) (рис.7а).
		ν
	В силу (62) эти функции распределения фактически описывают зависимость от
отношения		Г =γ / γ0 вероятности		P(γ ≥γ0 )	того, что случайный параметр				γ =γ (α1,α2 ) (58)
будет не ниже заданного порога γ0 .
	Как видно из рис.7б, с увеличением объема выборки δ вероятность								P(γ ≥γ0 )	растет
при	γ > γ0 ,	остается неизменной и равной			0.5	при γ = γ0	и уменьшается при			γ <γ0 .
Формальной причиной этого является трансформация плотности							pν (x) (59) (рис.7а), которая с
ростом δ		«стягивается» к точке		x =1 : ее среднее значение			ν)	(61) стремится к медиане
				0
					2	уменьшается. Это означает, что с ростом
(распределение «симметризуется»), а дисперсия σν)						уменьшается. Это означает, что с ростом
δ	реализации γ		концентрируются во все более узкой окрестности истинного значения γ ,
что увеличивает (уменьшает) вероятность превышения значением								γ порога γ0 , меньшего

<<< < Предыдущая 12 / 32 3 > Следующая >>>

Соседние файлы в папке Diss

#
27.03.201614.79 Mб68(Springer Series in Information Sciences 25) S. Haykin, J. Litva, T. J. Shepherd (auth.), Professor Simon Haykin, Dr. John Litva, Dr. Terence J. Shepherd (eds.)-Radar Array Processing-Springer-Verlag .pdf
#
27.03.20161.14 Mб451.pdf
#
27.03.201618.05 Mб12010.pdf
#
27.03.20161.14 Mб4511.pdf
#
27.03.2016438.53 Кб4412.pdf
#
27.03.2016951.5 Кб5313.pdf
#
27.03.2016120.99 Кб4916.pdf