2.2.4 Оценка значимости параметров регрессии

В линейной регрессии обычно оценивается значимость не только уравнения в целом, но и отдельных его параметров. С этой целью по каждому из параметров определяется его стандартная ошибка: т_b и т_а.

Стандартная ошибка коэффициента регрессии параметра b рассчитывается по формуле:

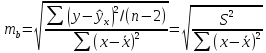
Где 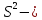остаточная дисперсия на одну степень свободы.

Отношение коэффициента регрессии к его стандартной ошибке дает t-статистику, которая подчиняется статистике Стьюдента при 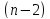степенях свободы. Эта статистика применяется для проверки статистической значимости коэффициента регрессии и для расчета его доверительных интервалов.

Для оценки значимости коэффициента регрессии его величину сравнивают с его стандартной ошибкой, т.е. определяют фактическое значение t-критерия Стьюдента: 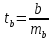, которое затем сравнивают с табличным значением при определенном уровне значимостиα и числе степе­ней свободы .

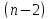Справедливо равенство

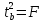
Доверительный интервал для коэффициента регрессии определяется как .

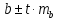Стандартная ошибка параметра а определяется по формуле

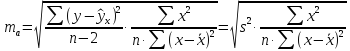
Процедура оценивания значимости данного параметра не отличается от рассмотренной выше для коэффициента регрессии: вычисляется t-критерий:

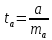
Его величина сравнивается с табличным значением при 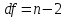степенях свободы.

Значимость линейного коэффициента корреляции проверяется на основе величины ошибки коэффициента корреляции m_r:

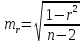
Фактическое значение t-критерия Стьюдента определяется как

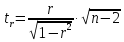
Данная формула свидетельствует, что в парной линейной регрессии 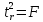, ибо как уже указывалось, 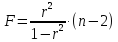. Кроме того,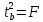, следовательно,.

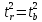Таким образом, проверка гипотез о значимости коэффициентов регрессии и корреляции равносильна проверке гипотезы о значимости линейного уравнения регрессии.

Рассмотренную формулу оценки коэффициента корреляции рекомендуется применять при большом числе наблюдений, а также если r не близко к +1 или –1.

2.3 Интервальный прогноз на основе линейного уравнения регрессии

В прогнозных расчетах по уравнению регрессии определяется предсказываемое y_р значение как точечный прогноз 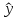_х при х_р = х_k т. е. путем подстановки в линейное уравнение регрессии 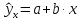соответствующего значения х. Однако точечный прогноз явно нереален, поэтому он дополняется расчетом стандартной ошибки 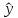_х, т. е. 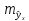, и соответственно мы получаем интервальную оценку прогнозного значения у*:

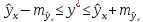
Считая, что прогнозное значение фактора х_р = х_k получим следующую формулу расчета стандартной ошибки предсказываемого по линии регрессии значения, т. е. 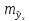имеет выражение:

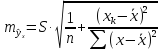
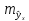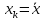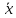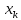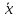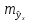Рассмотренная формула стандартной ошибки предсказываемого среднего значения у при заданном значении х_k характеризует ошибку положения линии регрессии. Величина стандартной ошибки достигает минимума при и возрастает по мере того, как «удаляется» от в любом направлении. Иными словами, чем больше разность междуи, тем больше ошибка, с которой предсказывается среднее значение у для заданного значения 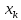. Можно ожидать наилучшие результаты прогноза, если признак-фактор х находится в центре области наблюдений х, и нельзя ожидать хороших результатов прогноза при удалении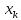. от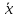. Если же значение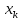. оказывается за пределами наблюдаемых значенийх, используемых при построении линейной регрессии, то результаты прогноза ухудшаются в зависимости от того, насколько 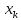. отклоняется от области наблюдаемых значений факторах.

На графике, приведенном на рис. 1, доверительные границы для 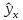представляют собой гиперболы, расположенные по обе стороны от линии регрессии. Рис. 1 показывает, как изменяются пределы в зависимости от изменения 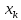.: две гиперболы по обе стороны от линии регрессии определяют 95 %-ные доверительные интервалы для среднего значенияу при заданном значении х.

Однако фактические значения у варьируют около среднего значения 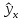. Индивидуальные значения у могут отклоняться от 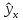на величину случайной ошибки ε, дисперсия которой оценивается как остаточная дисперсия на одну степень свободы 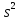. Поэтому ошибка предсказываемого индивидуального значенияу должна включать не только стандартную ошибку 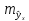, но и случайную ошибкуs.

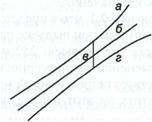
Рис. 1. Доверительный интервал линии регрессии:

а - верхняя доверительная граница; б - линия регрессии;

в — доверительный интервал для 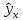при ;

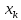г - нижняя доверительная граница.

Средняя ошибка прогнозируемого индивидуального значения у составит:

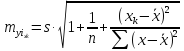
При прогнозировании на основе уравнения регрессии следует помнить, что величина прогноза зависит не только от стандартной ошибки индивидуального значения у, но и от точности прогноза значения фактора х. Его величина может задаваться на основе анализа других моделей исходя из конкретной ситуации, а также анализа динамики данного фактора.

Рассмотренная формула средней ошибки индивидуального значения признака у 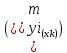может быть использована также для оценки существенности различия предсказываемого значения и некоторого гипотетического значения.

11