(Пример расчета)

Установлено, что средняя толщина серебряной оболочки не изменяется значимо по длине проволоки, а распределение толщин оболочки подчиняется закону Гаусса с отклонением s.

Исследуемым параметром является коэффициент вариации толщины серебряной оболочки проволоки диаметром 0,8 мм и исходного прессованного прутка диаметром 12 мм.

Обработка биметалла заключается в многократном волочении через твердосплавные, а далее алмазные волоки и промежуточных отжигах в электрических печах с воздушной атмосферой. Технологическая смазка при волочении - мыльная эмульсия. при исследовании имеется возможность варьировать степень относительного обжатия за проход и в известных пределах скорости волочения.

Актуальность снижения разнотолщинности определяется тем, что в готовой проволоке задана потребителем не средняя, а минимальная толщина оболочки серебра. Поскольку расход серебра пропорционален средней толщине оболочки, то снижение разнотолщинности позволяет уменьшить исходную толщину серебряной заготовки и расход серебра на производство проволоки. Основными факторами технологического процесса, влияющими на отношение М - коэффициента вариации толщины серебряной проволоки диаметром 0,8 мм и исходного прессованного прутка диаметром 12 мм являются:

Х1 - суммарная вытяжка между отжигами,

Х2 - температура промежуточного отжига ,^оС,

Х3 - длительность отжига.

Уровни и интервалы варьирования факторов

Фактор	Код	Уровни			Интервал варьирован.
		Верхн	Нулев	Нижн
Вытяжка,	Х1	15,2	9,55	3,9	5,65
Температура, ТоС	Х2	520	460	400	60
Время отжига, , час	Х3	1,0	0,75	0,5	0,25

Уравнение -модель процесса при планировании 2³ имеет вид:

для придания уравнению более общего вида добавим при дальнейшем рассмотрении эффекты тройных взаимодействий.

Xi -кодированные значения факторов

(А)

Искомая модель позволяет раздельно оценить не только влияние каждого фактора, но и влияние парных взаимодействий факторов.

Результаты экспериментов представлены в таблице 2.

Таблица 2.

Матрица планирования, результаты опытов и расчетов изменения разнотолщинности оболочки

№ u	Х0	Х1	Х2	Х3	Х1Х2	Х2Х3	Х1Х3	Х1Х2Х3
1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
1	+	+	+	+	+	+	+	+	2,02	2,21	2,115	0,01805	2,111	0,000016
2	+	-	+	+	-	+	-	-	1,91	1,90	1,905	0,00005	1,909	0,000016
3	+	+	-	+	-	-	+	-	1,75	1,62	1,685	0,00845	1,752	0,004489
4	+	-	-	+	+	-	-	+	2,42	2,34	2,380	0,00320	2,312	0,004624
5	+	+	+	-	+	-	-	-	1,82	2,05	1,935	0,02645	1,939	0,000016
6	+	-	+	-	-	-	+	+	1,77	1,71	1,740	0,00180	1,736	0,000016
7	+	+	-	-	-	+	-	+	2,35	2,37	2,360	0,00020	2,292	0,004624
8	+	-	-	-	+	+	+	-	2,75	2,82	2,785	0,00245	2,852	0,004484
												0,06065		0,018285

Для каждой строчки производится оценка дисперсии u-го опыта плана , повторяющегося с раз. Значение =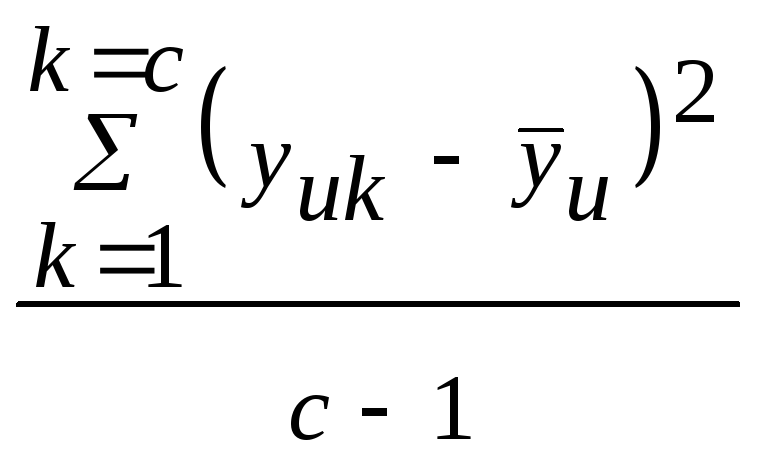, в знаменателе стоит число степеней свободы системы=с-1 (одна степень свободы была использована для определения среднего арифметического).

Сумма дисперсий для всех опытов: =0,06065. Оценить воспроизводимость каждого опыта можно по средней дисперсии=/N=0,06065/8=0,00758

Расчетное значение критерия рассчитывается по формуле:

G_р ==,

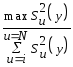Табличное значение G_р=0,6798 при ₁ =1, ₂ =8 при =0,05.

Таким образом, гипотеза об однородности дисперсий не отвергается.

Расчет коэффициентов модели ведется по формулам:

, ,,,

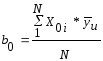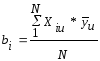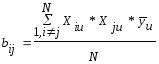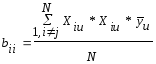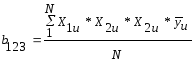
Результаты расчета коэффициентов представлены в таблице 3

2,1131	-0.0894	-0.1894	-0.0919
0.1906	0.1781	-0.0319	0.0356

Дисперсия ошибки при определении коэффициента модели:

=(75,8*10⁴)/(8*2)=0,0004737

или ==0,0218

Табличное значение t-критерия t_8;0,05=2,306, соответственно критическое значение коэффициента модели:

=2,306*0,0218=0,0502, т.е. все коэффициенты, большие по модулю критического значения будут статистически незначимыми.

Коэффициенты иприX₁X₃ и X₁ X₂ X₃ признаны незначимыми.

Полученная модель имеет вид.

М=Y=2,1131-0,0894Х₁-0,1894X₂-0,0919X₃+0,1906X₁X₂+0,1781X₂X₃)

После подстановки кодированных значений Х_i в полученное уравнение модели, получим столбец расчетных значений

Проверка адекватности модели оценивает отклонение предсказанных полученным уравнением регрессии значений от средних экспериментальных значений каждого опыта=0,01829/(8-5)=0,006097, гдеm - число значащих членов уравнения регрессии.

Дисперсия сравнивается со средней дисперсией или дисперсией воспроизводимости. ОтношениеF=/ сопоставляется с табличным значением F критерия со степенями свободы (N-m) для числителя -1 и

(N*(c-1)) для знаменателя - 2.

F=0,006097/0,00758=0,8043.

F табл. =4,07 при степенях свободы 8-5=3 и N*(c-1)=8

F табл. >F расч., поэтому модель признана адекватной.

В заключение преобразуем полученное уравнение к натуральным переменным. Для этого воспользуемся формулой А и таблицей, характеризующей факторное пространство.

Полученная модель будет иметь вид:

М=10,56-0,275-0,018-5,83+0,0006+0,012