4. Условия кодирования переменных

Удобнее работать с переменными, если они закодированы и являются «безразмерными» величинами. При этом они изменяются от –1 до +1. При этом можно достичь унификаци при обработки данных. Для каждого фактора Х_i интервал варьирования будет определен как:

Значение переменных в центре факторного пространства определяется:

Текущее значение кодированной i-той переменной :

При использовании кодированных переменных модель будет строиться в унифицированном виде.ю независимо от ее физического содержания. После нахождения уравнения регрессии для перехода к физической модели достаточно перйти от кодированных переменных к физическим, используя соответствующие формулы.

5. Вид уравнения регрессии

В планировании эксперимента каждый исследуемый параметр y_k принято представлять как функцию отклика, которая может аппроксимироваться линейным

неполным квадратным

или квадратным уравнением вида:

где: b_o, b_i, b_ij, b_ii- коэффициенты уравнения регрессии,

х_i, х_j-переменные факторы,

х_о- фиктивная переменная, необходимая для определения свободного члена.

Для проведения экспериментальных исследований выберем факторный эксперимент типа 2⁴, позволяющий оценить коэффициенты линейных членов и эффекты парных взаимодействий различных факторов.

6. Последовательность выполнения опытов

Если опыты реализовать в той последовательности, в какой они обычно располагаются в матрице планирования, возможно получение систематической ошибки, обусловленной влиянием внешних факторов: притуплением реакции восприятия экспериментатора, дрейф показаний приборов в течение рабочего цикла. Для нивелирования ошибки опыты рандомизируются, те есть выполняются в случайном порядке. Каждый из опытов повторяется по три раза.

7. Матрица планирования

При планировании эксперимента принята табличная (матричная) форма записи условий проведения опытов. Знак «+» в соответствующей строке матрицы планирования означает, что эксперимент проводится при верхнем (максимальном) значении данного фактора, знак «-» - на нижнем (минимальном). В уравнении регрессии это соответствует множителю «+1» или «-1» соответственно.

В соответствии с этими обозначениями матрица планирования 2 ⁴представлена на таблице 1.

В столбцах 7, 8, 9, 10 представлены значения y, полученные, при проведении дублирующихся опытов, в столбце 11 среднее значение по проведенным опытам, в столбце 12 - величина дисперсии по каждой серии опытов.

Значения в столбце 11 рассчитываются по формуле: =

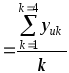
Значения =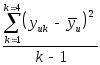, в знаменателе стоит число степеней свободы системы=к-1 (одна степень свободы была использована для определения среднего арифметического) .