7.1.2. Способ замены плоскостей проекций в проекциях с числовыми отметками Теоретическая часть
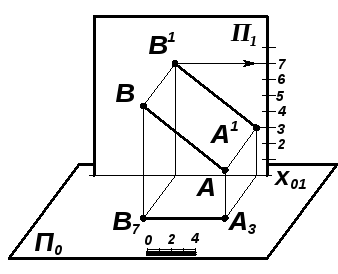
прямую общего положения преобразовать в прямую уровня, если новую плоскость ввести параллельно прямой (рис.7.11);
|
|
|
|
Рис. 7.11 | |
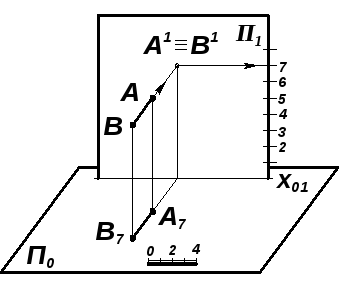
прямую уровня преобразовать в проецирующую прямую, если новую плоскость ввести перпендикулярно прямой (рис. 7.12);
|
|
|
|
Рис. 7.12 | |
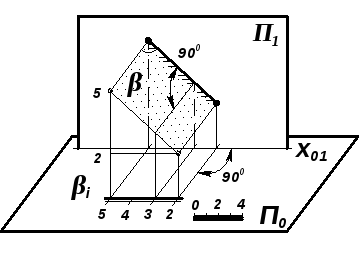
плоскость общего положения преобразовать в проецирующую, если новую плоскость выбрать перпендикулярно горизонтали заданной плоскости (рис. 7.13):
|
|
|
|
Рис. 7.13 | |
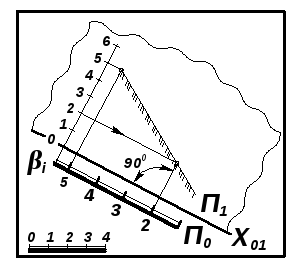
проецирующую плоскость преобразовать в плоскость уровня, если новую плоскость ввести параллельно заданной плоскости (рис. 7.14):
|
|
|
|
Рис. 7.14 | |
ЗАДАЧИ
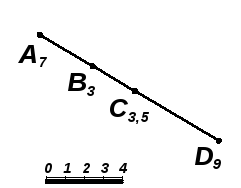
Задача 7.6. Провести линию из точки В7, перпендикулярную плоскости, заданной масштабом уклонов βi, и определить отметку точки А пересечения с ней (рис. 7.15).
|
|
|
|
Рис. 7.15 | |
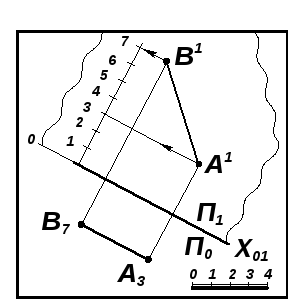
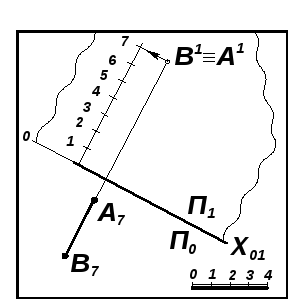
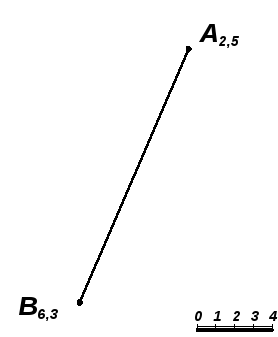
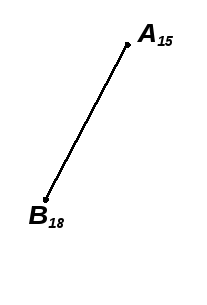
Задача 7.6. Определить натуральную величину отрезка АВ и углы его наклона к плоскости П0 (рис. 7.16; 7.17).
|
|
|
|
|
|
|
Рис. 7.16 |
Рис. 7.17 |
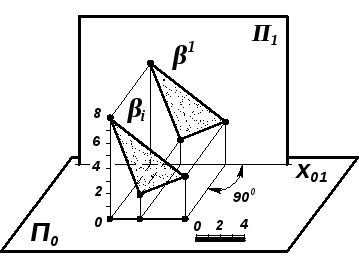
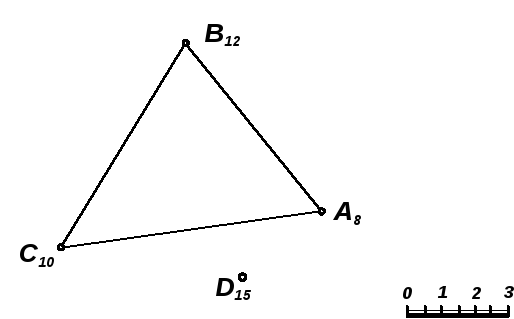
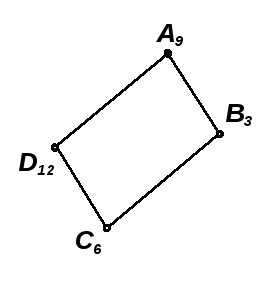
Задача 7.7. Определить расстояние от точки D15 до плоскости, заданной треугольником А8 В12 С10 (рис. 7.18).
|
|
|
Рис. 7.18 |
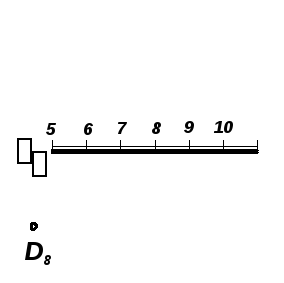
Задача 7.8. Определить расстояние от точки D8 до плоскости, заданной масштабом уклонов βi (рис. 7.18).
|
|
|
|
Рис. 7.18 | |
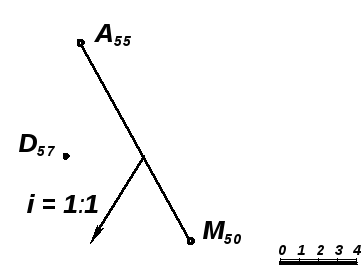
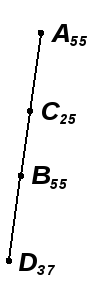
Задача 7.9. Определить расстояние от точки D57 до плоскости, заданной отрезком прямой А55 M50 и уклоном i = 1:1 (рис. 7.19).
|
|
|
Рис. 7.19 |
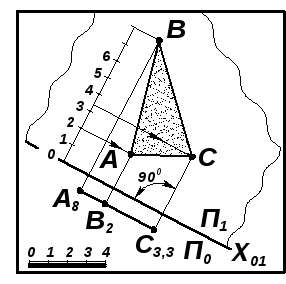
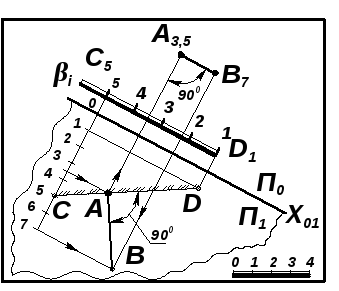
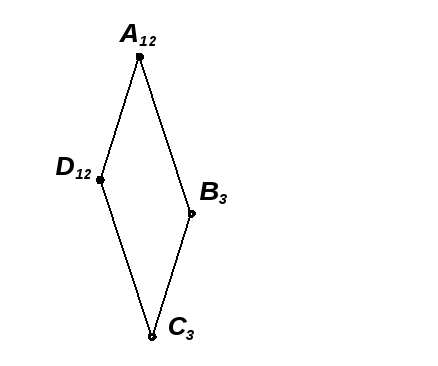
Задача 7.10. Определить натуральную величину четырехугольной плиты АВСD (рис. 7.20; 7.21).
|
|
|
|
| |
|
Рис. 7.20 |
Рис. 7.21 |
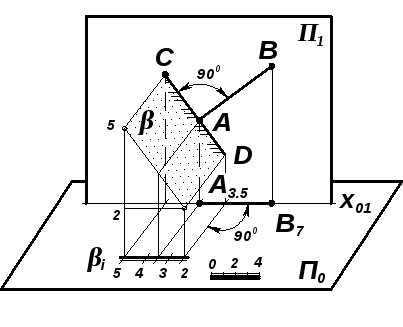
Задача 7.11. Определить угол наклона четырехугольной плиты АВСD к плоскости П0 (рис. 7.22; 7.23).
|
|
| |
|
|
| |
|
Рис. 7.22 |
Рис. 7.23 | |
7.1.3. Контрольные вопросы
ортогональные проекции
Сущность способа замены плоскостей проекции.
Как располагается новая плоскость проекций относительно имеющихся плоскостей при использовании способа замены плоскостей проекций?
Какие построения выполняются, чтобы прямую уровня преобразовать в проецирующую прямую?
Какие построения выполняются, чтобы прямую общего положения преобразовать в прямую уровня?
Какие построения выполняются, чтобы плоскость общего положения преобразовать в плоскость проецирующую?
Какие построения выполняются, чтобы проецирующую плоскость преобразовать в плоскость уровня?
Последовательность замены двух плоскостей, чтобы плоскость общего положения преобразовать в плоскость уровня.
проекции с числовыми отметками
Как располагается новая плоскость проекций относительно плоскости нулевого уровня при использовании способа замены плоскостей проекций?
Какие построения выполняются, чтобы прямую общего положения преобразовать в прямую уровня?
Почему в строительстве применяется преобразование прямой или плоскости в положение уровня?
Почему в строительстве новую плоскость называют профилем?