5.Теорема Куна-Таккера, следствие из нее.

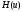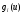Теорема Куна-Таккера. Пусть и дифференцируемы по в области U и - точка максимума для, при ограничении 0. Тогда существуют такие неотрицательные числа0, что выполняется следующее равенство:

Причем=0 для всехiдля которых.( то есть для неэффективных ограничений.) Причем>0 для всехiдля которых.( то есть для эффективных ограничений.)

Доказательство:

Пусть точки максимума для.

Надо рассмотреть два случая:

1. Случай внутренней точки. Пусть — внутренняя точка. Тогда положим все= 0, т.к. ограничения будут неэфективны.производная ф-ии в точке экстремума

2. и* — граничная точка. Проведем через точку опорную гиперплоскость Г, и направим все нормали по градиенту функции. Можно записать следующее соотношение:

= 0, так как ограничение неэффективно (то есть данная точка этому ограничению не принадлежит).

Следствие 1. Если дифференцируема по в области U, а — точка, где достигает своего максимума, то для всех направлений, допустимых в этой точке выполняется следующее неравенство .

1. Если - внутренняя точка, то

2. Если — граничная точка, то выполняется условие теоремы Куна-Таккера.

Следствие 2. Если функции H вогнута относительно управления, то необ­ходимое условие оптимальности оказывается и достаточным. Найденное в этом случае управление оказывается оптимальным в глобальном смысле, т.к. экстремум такой функции — максимум, причём единственный.

6.Теорема о числе переключений.

Если

1. Задана система обыкновенных дифференциальных уравнений вида

2. Матрице А имеет все вещественные собственные значения

3. На управление наложены следующие ограничения вида ,j=1,..,m

то число переключений функции оптимального по быстродействию управления не превышает n-1, где n – порядок исходной системы.

Доказательство: Запишем закон движения объекта в следующем виде

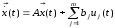
Оптимальное управление Куна-Таккера определяется следующим образом:

В этом выражении функция ψ(t) может быть определена из следующего диф.уравнения

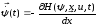
H –функция Гамильтона

Т.е. нам нужно найти производную по х:

Решение имеет вид — начальное значение в момент времениt0 = 0. Один из способов задания — нормаль к опорной гиперплоскости в точке х(t0)

Перепишем выражение для оптимального управления с учётом ψ(t):

Представим e^At в виде спектрального разложения e^At = ρe^λtρ−¹, где р, ρ−¹ — матрицы правых и левых собственных векторов.

Если воспользуемся матричным свойством C = AB => С −¹ = B−¹A−¹, получим

Значит, оптимальное управление будет определятся как

— некоторые коэффициенты, которые опредляются матрицами ρ и ρ−¹ и векторами bj и ψ₀ и не зависят от времени. Тогда моменты переключения управления — это моменты, когда выражения под знакомsign’ма равно 0. Число переключений определяется корнями этого выражения:=0.

Рассмотрим случай, когда n = 2. При суммировании экспонент будет либо одно пересечение c осью времени, либо не будет ни одного. По индукции можно доказать, что сумма n экспонент будет иметь не более (n − 1) пересечений с осью времени.

Замечание. Данная теорема верна только в случае действительных корней матрицы A. При комплексных корнях появится функция sin, и следовательно, пересечений будет бесконечно много.

Таким образом, мы нашли оптимальное управление как функцию ψ(t)

Чтобы ее определить, нужно решить систему дифференциальных уравне­ний:

при граничных условиях x(t₀) и x(t_f) = 0. Найдя из нее ψ(t) и подставив в выражение оптим-го управления, мы получаем u^*_j как ф-цию времени.

Т.о., задача определения оптимального управления сводится к решению нели­нейной системы уравнений. Для высоких порядков она решается чис­ленно. Если n = 2, то решение может быть получено с помощью метода фазовой плоскости.