
Методичка по физике.Лабораторные работы
.pdfФедеральное агентство по атомной энергии Cеверская государственная технологическая академия
ФИЗИЧЕСКИЙ ПРАКТИКУМ
Часть 3
ОПТИКА. АТОМНАЯ ФИЗИКА
Северск 2006
УДК 530 (076.5)
Физический практикум. Часть 3.Оптика. Атомная физика: Учебное пособие. – Северск: Изд. СГТА, 2006. – 116 с.
Физический практикум содержит описание девяти лабораторных работ по курсу «Оптика. Атомная физика».
Цель настоящего практикума – привить студентам навыки самостоятельной работы с приборами и установками, ознакомить с методами измерения изучаемых физических величин. Выполнение лабораторных работ должно способствовать более глубокому пониманию изучаемых физических явлений и закономерностей.
Учебное пособие написано в соответствии с программой по курсу общей физики и предназначено для студентов и преподавателей технических ВУЗов.
Рецензенты:
А.И. Потекаев |
профессор ТГУ, д.ф.-м.н. |
В.А. Власов |
профессор ТПУ, д.ф.-м.н. |
Темплан 2005
2
|
СОДЕРЖАНИЕ |
|
||
Введение . . . . . . . . . . . . . . . . |
. . . . . . . . . |
. . . . . . . . . . . . . . . . . . . . . |
4 |
|
1 |
Лабораторная работа 35. |
Измерение показателя преломления |
|
|
растворенного вещества с помощью интерферометра. . . . . . . . . . . . . |
5 |
|||
2 |
Лабораторная работа 36. Определение длин световых волн с |
|
||
помощью дифракционной решетки. . . . . . . . |
. . . . . . . . . . . . . . . . . . . . . . |
16 |
||
3 |
Лабораторная работа 37. Определение концентрации сахара |
|
||
сахариметром. . . . . . . . . . . . . . . . . |
. . . . . . . . . |
. . . . . . . . . . . . . . . . . . . . . . |
27 |
|
4 |
Лабораторная работа 41. Исследование дисперсии стеклянной |
|
||
призмы. . . . . . . . . . . . . . . . . . . . . . |
. . . . . . . . . |
. . . .. . . . . . . . . . . . . . . . . . . . |
37 |
|
5 Лабораторная работа 44. Изучение |
фотоэлемента с внешним |
|
||
фотоэффектом . . . . . . . . . . . . . . . |
. . . . . . . . . . |
. . . . . . . . . . . . . . . . . . . . . . . |
54 |
|
6 |
Лабораторная работа 45. Определение постоянной Стефана- |
|
||
Больцмана и постоянной Планка |
. . . . . . . . . |
. . . . . . . . . . . . . . . . . . . . . . . |
67 |
|
7 |
Лабораторная работа 46. |
Изучение серии Бальмера и |
|
|
постоянной Ридберга. . . . . . . . . . |
. . . . . . . . . |
. . . . . . . . . . . . . . . . . . . . . . |
77 |
|
8 |
Лабораторная работа 47. Изучение |
интерференции и |
|
|
дифракции света с помощью лазера . . . . . . . |
. . . . . . . . . . . . . . . . . . . . . |
89 |
||
9 |
Лабораторная работа 51. Опыт Франка и Герца (Определение |
|
||
первых потенциалов возбуждения инертных газов). . . . . . . . . . . . . . .. |
105 |
|||
3
Введение
Учебное пособие «Физический практикум. Часть 3 Оптика. Атомная физика» содержит методические указания по выполнению девяти лабораторных работ по курсу «Оптика и Атомная физика». Авторы учебного пособия создали пособие, позволяющее на практике познакомиться с такими физическими явлениями, как дифракция и интерференция, поляризация и дисперсия, тепловое излучение и фотоэффект. Выполнение лабораторных работ способствует более глубокому пониманию изучаемых физических явлений и закономерностей.
В методическом указании по каждой лабораторной работы содержатся определение цели работы, теоретическое введение, которое помогает усвоению материала при подготовке к занятию, описание лабораторной установки и приборов, порядок выполнения работы, контрольные вопросы, список рекомендуемой литературы.
Настоящий практикум ставит своей целью помочь студентам в организации самостоятельной работы по подготовке к лабораторным занятиям, привить студентам навыки проведения экспериментального исследования, приобрести опыт работы с приборами и установками, ознакомить их с методами измерения изучаемых физических величин.
Общий объем и содержание учебного пособия отвечают требованиям государственного образовательного стандарта высшего профессионального образования для инженерных специальностей высших учебных заведений.
Учебное пособие написано в соответствии с программой курса общей физики и предназначено для студентов и преподавателей технических ВУЗов.
4
1 Исследование явления интерференции световых волн с помощью интерферометра Рэлея
1.1 Цель работы
Изучение явления интерференции света, устройства и принципа работы интерферометра Рэлея. Определение показателя преломления и неизвестной концентрации растворенного вещества с помощью интерферометра Рэлея.
1.2 Теоретическая часть
1.2.1 Интерференция колебаний. Когерентность
Рассмотрим сложение двух гармонических колебаний с одинаковой частотой ω , происходящих в одном направлении:
a1 = a01 sin(ωt +α1 ), a2 = a02 sin(ωt +α2 ) ,
где a01 и a02 – амплитуды колебаний; α1 и α2 – начальные фазы
колебаний; t – время. В результате сложения этих колебаний вновь образуется гармоническое колебание:
a = a0 sin(ωt +ϕ),
где амплитуда a0 и разность фаз ϕ определяются выражениями:
a02 = a012 + a022 + 2a01a02 cos(α1 −α2 ),
tgϕ = a01 sin((α1 ))+ a02 sin((α2 )).
a01 cos α1 + a02 cos α2
Результат сложения колебаний зависит от разности фаз δ =α2 −α1
исходных колебаний. Амплитуда результирующего колебания a0 может |
|||||||||
принимать |
любое значение в интервале от |
(a01 −a02 )2 при δ =π |
до |
||||||
(a01 + a02 )2 |
при δ = 0 . |
|
|
|
|
|
|
||
|
Энергетической характеристикой колебаний является физическая |
||||||||
величина - интенсивность I , |
значение |
которой |
пропорционально |
||||||
квадрату амплитуды |
(I a2 ). Вычислим среднее |
за промежуток времени |
|||||||
|
|
|
0 |
|
|
|
|
|
|
τ |
значение квадрата амплитуды: |
|
|
|
|
|
|
||
|
|
|
τ |
+ a022 + 2a01a02 τ1 |
τ |
|
|
|
|
|
|
a02 |
= τ1 ∫a02dt = a012 |
∫cos(δ )dt . |
(1.1) |
||||
Если разность фаз δ |
0 |
|
|
0 |
|
|
|
||
имеет случайный характер и за промежуток времени |
|||||||||
τ |
она многократно |
принимает значения в интервале |
от |
0 до 2π , |
то |
||||
|
τ |
|
|
|
|
|
|
|
|
интеграл ∫cos(δ )dt стремится к нулю. В этом случае |
a02 |
определяется |
|||||||
|
0 |
|
|
|
|
|
|
|
|
выражением: |
a02 |
= a012 + a022 . |
|
|
|
|
|
||
5
Соответственно интенсивность I |
результирующих колебаний равна сумме |
|||||||||||
интенсивностей I1 |
и I2 исходных колебаний: |
|
|
|||||||||
|
|
|
|
|
|
|
I = I1 + I2 . |
|
|
|
||
Если разность фаз δ |
не зависит от времени, то выражение (1.1) принимает |
|||||||||||
вид: |
|
|
|
|
|
|
|
|
|
|
cos(δ ). |
|
|
|
|
|
a2 |
= a |
2 |
+ a2 |
+ 2a |
a |
02 |
|
|
|
|
|
|
0 |
|
01 |
02 |
01 |
|
|
|
|
В этом случае интенсивность I |
результирующих колебаний в зависимости |
|||||||||||
от разности фаз δ |
может быть больше или меньше суммы интенсивностей |
|||||||||||
исходных колебаний: |
|
|
|
|
|
|
|
|
||||
|
|
|
|
I = I1 + I2 + 2 I1 I2 cos(δ ). |
(1.2) |
|||||||
Колебания, |
при сложении которых I ≠ I1 + I2 , |
называются когерентными. |
||||||||||
Явление усиления или ослабления интенсивности колебания в результате |
||||||||||||
сложения когерентных колебаний называется интерференцией |
||||||||||||
колебаний. |
|
|
|
|
|
|
|
|
|
|
|
|
1.2.2 Интерференция световых волн. Условия максимума и |
||||||||||||
минимума |
|
|
|
|
|
|
|
|
|
|
|
|
По аналогии с определениями пункта 1.2.1 принято говорить об |
||||||||||||
интерференции волн, если при их сложении не имеет места |
||||||||||||
суммирование интенсивностей. Очевидно, что возможна интерференция |
||||||||||||
только когерентных волн с одинаковой частотой, направления колебаний |
||||||||||||
которых совпадают. Под когерентностью волн понимается постоянство |
||||||||||||
разности фаз. Рассмотрим интерференцию двух световых волн. |
|
|||||||||||
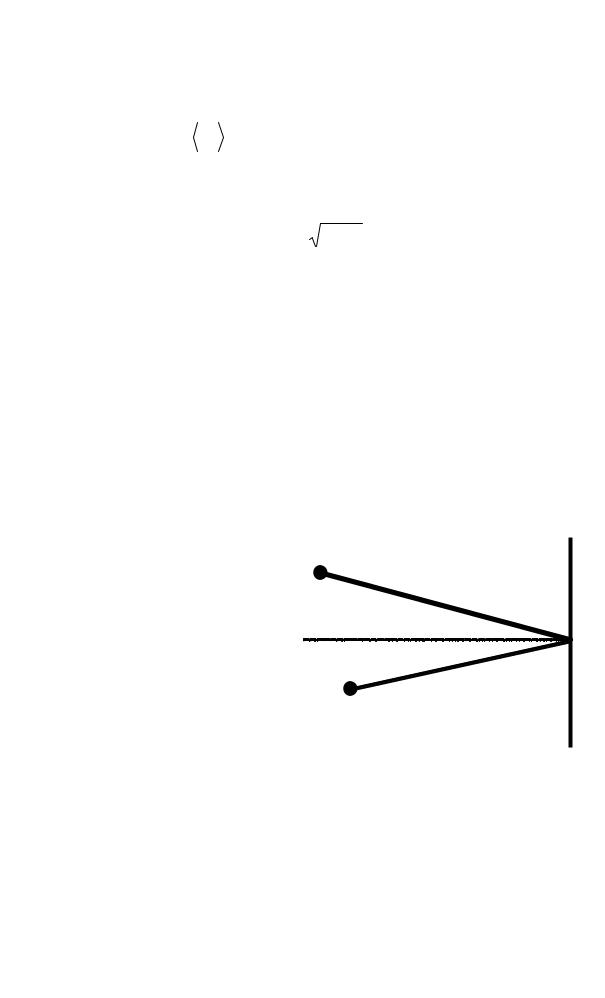
Пусть |
|
два |
|
точечных |
|
S2 |
|
|
|
Э |
||
источника |
|
света |
|
S1 и S2 |
|
|
|
|
|
|
||
(рисунок |
|
1.1) |
|
излучают |
|
|
|
|
l2 |
|
||
монохроматические |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
n2 |
|
||||
плоскополяризованные |
|
|
|
|
|
|
P |
|||||
|
|
|
|
|
|
|
||||||
световые волны с одинаковой |
|
|
|
|
n1 |
|||||||
|
|
|
|
|
||||||||
частотой |
|
ω |
и |
нулевой |
|
|
|
|
|
|||
|
|
|
|
|
l1 |
|
||||||
начальной |
|
фазой |
α1 =α2 |
= 0 . |
|
S1 |
|
|
|
|||
Причем |
пусть |
|
плоскости |
|
|
|
|
|
||||
|
|
|
|
|
|
|
||||||
поляризации |
|
|
совпадают. |
Рисунок 1.1 – Схема получения интерференци- |
||||||||
Определим |
|
интенсивность |
||||||||||
света IP в |
|
точке экрана |
Р в |
онной картины от двух точечных источников |
||||||||
результате сложения световых |
|
|
|
|
|
|
||||||
волн от первого и второго |
|
|
|
|
|
|
||||||
источников света в момент времени t . Колебания напряженности |
||||||||||||
электрического |
поля E1,P (в |
плоскости |
колебаний) |
в точке Р, |
||||||||
создаваемые |
световой |
волной, |
испускаемой первым |
источником |
||||||||
света S1,определяются выражением: |
|
|
|
|
|
|||||||
|
|
|
|
|
E1,P = E01sin(ω(t −t1 )) , |
|
||||||
6 |
|
|
|
|
|
|
|
|
|
|
|
|

где E01 – амплитуда колебаний напряженности электрического поля в световой волне, излучаемой источником S1; t1 – время, за которое волна
проходит от источника света S1 до точки Р. Аналогично, колебания напряженности электрического поля E2,P в точке Р, создаваемые световой
волной, испускаемой источником света S2 , определяются выражением:
E2,P = E02sin(ω(t −t2 )),
где E02 – амплитуда колебаний напряженности электрического поля в световой волне, излучаемой источником S2; t2 – время, за которое свет от
источника света S2 достигает точки Р. Учитывая, что свет от первого источника распространяется в среде с показателем преломления n1 , а свет
от второго источника - в среде с показателем n2 , значения t1 и t2 можно найти по формулам:
|
|
|
|
t = |
l1 |
= |
l1 |
n , |
t |
|
= |
l2 |
= |
l2 |
n , |
|
|
|
|
|
v |
c |
|
|
c |
||||||||
|
|
|
|
1 |
|
1 |
|
2 |
|
v |
2 |
|
2 |
|||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
где l |
1 |
и l |
2 |
– расстояния от источников S1 |
и S2 до точки наблюдения Р; v |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
||
и v2 – фазовая скорость света в среде с показателем преломления n1 и n2
соответственно; c – скорость света в вакууме. Таким образом, |
разность |
|||||
фаз δP колебаний, создаваемых волнами, излучаемыми источниками S1 и |
||||||
S2 в точке Р, равна: |
|
= ω (l n −l |
|
|
|
|
δ |
P |
n |
). |
(1.3) |
||
|
c |
1 1 |
2 |
2 |
|
|
|
|
|
|
|
|
|
Произведение расстояния, пройденного электромагнитной волной в среде, на показатель преломления этой среды называется оптической длиной
пути. |
Учитывая, |
что |
ω c = 2π λ |
( λ – длина волны в вакууме), |
|||
выражение (1.3) можно переписать в виде: |
|
|
|||||
|
|
|
δP = |
2π |
|
, |
|
|
=(l1n1 −l2n2 ) |
|
λ |
|
|||
|
|
|
|
|
|||
где |
– оптическая разность хода. |
|
|||||
|
Если оптическая разность хода |
равна целому числу длин волн λ, |
|||||
то есть |
=± m λ |
(m = 0,1, 2,K), |
(1.4) |
||||
|
|
||||||
то разность фаз δP |
кратна |
2π и лучи приходят в точку Р с одинаковой |
|||||
фазой. При выполнении условия (1.4) интенсивность света в точке Р будет иметь максимальное значение Imax , равное, согласно формуле (1.2)
|
Imax |
= I1 + I2 + 2 I1 I2 , |
|
|||
где I1 и I2 – интенсивности света, испускаемого источниками S1 и S2. Если |
||||||
оптическая разность хода |
равна полуцелому числу длин волн λ : |
|
||||
|
|
1 |
|
(m = 0,1, 2,K), |
(1.5) |
|
=± m + |
|
λ |
||||
2 |
||||||
|
|
|
|
|
||
то разность фаз δP равна нечетному числу π и лучи приходят в точку Р в
7
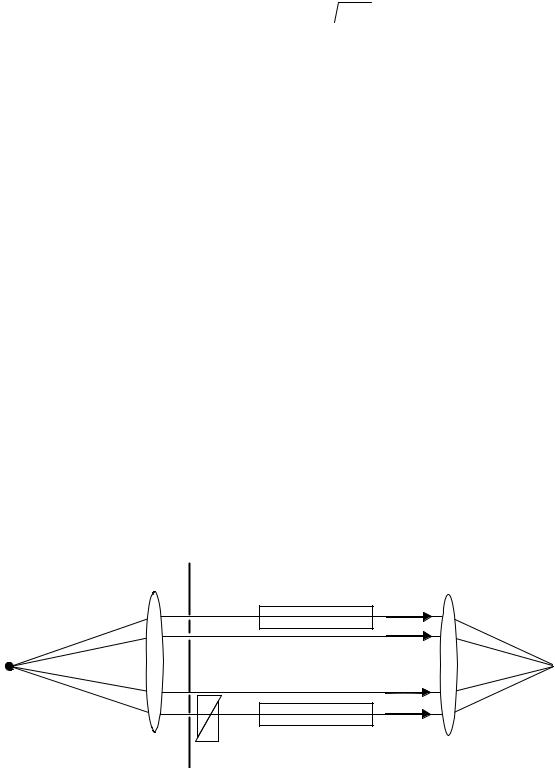
противофазе, и результирующая интенсивность света будет минимальна:
Imin = I1 + I2 − 2 I1 I2 .
I1 I2 .
Выражения (1.4) и (1.5) называются условиями интерференционного максимума и минимума соответственно.
Из проведенного анализа следует, что интенсивность света на экране Э при сложения волн, испускаемых источниками S1 и S2 , может принимать значения в диапазоне от Imin до Imax . Значение интенсивности в
конкретной точке будет определяться оптической разностью хода световых волн. Таким образом, в результате интерференции световых волн, излучаемых источниками света S1 и S2 , на экране Э будет наблюдаться чередование светлых и темных полос. Описанное распределение интенсивности называется интерференционной картиной.
1.2.3 Интерферометр Рэлея
Интерференционная картина чрезвычайно чувствительна к малейшим изменениям условий ее получения. Незначительное изменение оптической разности хода (порядка долей длины волны) может привести к существенному изменению интерференционной картины (смещению полос). Это свойство используется для создания специальных приборов – интерферометров, основанных на зависимости интерференционной картины и позволяющих проводить очень точные измерения. Интерферометр Майкельсона позволяет с точностью до 10–7м определять длины. Интерферометр Линника позволяет исследовать качество обработки поверхностей. Интерферометр Жамена позволяет измерять близкие к единице показатели преломления. Для анализа газов или жидкостей применяется интерферометр Рэлея, принципиальная схема
L1 C |
A |
L2 |
|
1 |
|
|
|
3 |
O |
S |
4 |
2
B
K
Рисунок 1.2 – Оптическая схема интерферометра Рэлея
которого приведена на рисунке 1.2.
Свет, излучаемый источником S, проходя через линзу L1 щели С, разделяется на четыре параллельных луча. Лучи 1 и 2 проходят через одинаковые кюветы: А – заполненную исследуемым веществом, и В – заполненную веществом с известным показателем преломления. Кроме
8

этого, луч 2 проходит через клиновой компенсатор К. Лучи 3 и 4 проходят мимо камер А и В. Все лучи попарно (первый со вторым, третий с четвертым) собираются линзой L2 и создают в разделенном пополам объективе О две интерференционные картины (рисунок 1.3). Положение интерференционных полос, создаваемых третьим и четвертым лучами, постоянно. Различие показателей преломления веществ в кюветах
приводит к появлению оптической разности хода |
: |
= (nA −nB )d , |
(1.6) |
где nA и nB – показатели преломления веществ, заполняющих кюветы А и
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В; d – длина кюветы. Появление оптической |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
разности хода приводит к смещению |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
создаваемой первым и вторым лучами |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
интерференционной |
картины, |
измеряя |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
величину отклонения которой, можно найти |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
показатель |
преломления |
исследуемого |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
вещества. Для измерения величины |
служит |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
клиновой компенсатор К, состоящий из двух |
||||
Рисунок 1.3 – Интерферен- |
клиньев, |
образующих |
плоскопараллельную |
|||||||||||||||||||||
ционные картины |
пластину. |
Сдвигая |
один |
из |
клиньев |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
относительно другого, можно установить |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
такую |
толщину |
l |
получающейся |
|
плоскопараллельной пластинки, что создаваемая ей разность оптического хода будет компенсировать разность хода , создаваемую кюветами. В этом случае интерференционные картины, создаваемые различными лучами, совпадут. Таким образом, зная показатель преломления вещества, из которого сделан компенсатор nK и длину l, можно рассчитать
величину
= nK l,
а затем из формулы (1.6) найти показатель преломления исследуемого вещества.
1.3 Вывод рабочих формул
1.3.1 Формула для вычисления показателя преломления растворенного вещества
Согласно классической электронной теории дисперсии, величина r , называемая удельной рефракцией, является постоянной для каждого вещества. Связь удельной рефракции вещества с его показателем преломления n определяется формулой Лоренц – Лорентца:
r = |
n2 |
−1 |
|
1 |
, |
(1.7) |
|
n2 + 2 |
ρ |
||||||
|
|
|
|
||||
где ρ – плотность вещества. Опыт показывает, что удельная рефракция
9

смеси двух веществ R , имеющих удельные рефракции r1 и r2 , равна:
R =C1r1 +C2r2 , |
(1.8) |
где C1 и C2 – объемная доля первого и второго веществ в растворе.
Учитывая, что объемной долей вещества в растворе называется отношение объема, занимаемого молекулами данного вещества, к полному объему раствора, верно соотношение:
1 = |
V1 |
+ |
|
V2 |
=C +C |
2 |
, |
|
|
||||||
|
V1 +V2 |
|
1 |
|
|||
где V1 и V2 – объемы, |
|
V1 +V2 |
|
|
|||
занимаемые молекулами первого и второго |
|||||||
вещества. Тогда выражение (1.8) можно переписать в виде: |
|||||||
|
R =(1 −C2 )r1 +C2 r2 . |
|
(1.9) |
||||
Пусть известны показатель преломления раствора n , растворителя n1, плотности растворенного вещества ρ2 , растворителя ρ1 и объемная доля растворенного вещества C2 . Получим выражение для показателя преломления растворенного вещества n2 . Из формулы Лоренца –
Лорентца (1.7) выразим n2 через удельную рефракцию r2 : |
|
|||||||||||||||
n |
= |
|
1+ 2 r2 ρ2 . |
(1.10) |
||||||||||||
2 |
|
|
|
|
1−r2 |
ρ2 |
|
|||||||||
Значение удельной рефракции r2 |
|
|
|
|
|
|||||||||||
|
растворенного вещества можно найти из |
|||||||||||||||
выражения (1.9): |
|
|
R −(1−C2 )r1 |
|
|
|||||||||||
r = |
. |
(1.11) |
||||||||||||||
|
|
|
|
|
|
|
||||||||||
2 |
|
|
|
|
|
C2 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Значения удельных рефракций раствора R и растворителя r1 |
определяются |
|||||||||||||||
соотношениями: |
|
|
|
|
n2 −1 |
|
|
1 |
|
|
|
|
||||
R = |
|
|
, |
|
(1.12) |
|||||||||||
|
|
|
|
|
||||||||||||
|
|
|
|
|
n2 |
+ 2 ρ |
|
|
|
|
||||||
r |
|
= |
|
n2 |
−1 |
1 |
|
. |
|
(1.13) |
||||||
|
1 |
|
|
|
|
|
|
|
|
|||||||
|
n2 |
+ 2 |
|
|
|
ρ |
|
|
|
|||||||
1 |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
||
Плотность раствора ρ определяется выражением: |
|
|||||||||||||||
ρ =(1−C2 )ρ1 +C2 ρ2 . |
(1.14) |
|||||||||||||||
1.4 Экспериментальная часть
1.4.1 Безопасность труда
В работе используется интерферометр ЛИР–2, подключаемый к сети переменного тока 220В. При выполнении работы необходимо надежно заземлить приборы.
10
