3.3. Свертка функций

Свертка функций – это важнейшее математическое понятие, которое используется почти во всех областях науки и техники, в том числе, оно широко применяется для оценки систем изображения и для процессинга цифровых изображений. Свертка двух функций – это математическая операция двух функций h(x) и f(x), порождающая третью функцию g(x), которая может рассматриваться как модифицированная версия одной из первоначальных, например, после операций осреднения или сглаживания. Свертка h(x) и f(x) записывается как h∗f (символ звездочки). Для непрерывных функций она определяется как интеграл от произведения двух функций после того, как одна реверсируется и смещается. По существу, это особый вид интегрального преобразования:

(5.9)

Операция свертки иллюстрируется на рис. 5.8 для двух функций, заданных в виде прямоугольных импульсов разной длительности.

Рис. 5.8. Пример свертки двух непрерывных функций h(x) и f(x). Более темным цветом показана площадь, равная интегралу (5.9) при разных значениях x (адаптировано из [4])

Одномерная дискретная свертка двух дискретных функций h(i) и f(i) длиной N определяется как

(5.10)

С точки зрения вычислительного процесса более легким и быстрым способом расчета свертки двух функций является использование теоремы свертки. В этой теореме доказывается, что свертка двух функций эквивалентна перемножению их преобразований Фурье в частотном пространстве. Таким образом, уравнение свертки (5.9) можно выразить в виде

(5.11)

где H(u) и F(u) – преобразование Фурье функций h(x) и f(x) в частотном пространстве.

3.4. Дискретные преобразования Фурье

Для преобразования дискретной формы изображения в частотной пространство традиционно применяется дискретное преобразование Фурье (ДПФ, англ. DFT). Двумерное прямое и обратное дискретные преобразования Фурье для выборки N × N пикселей изображения [f(m,n)] записываются следующим образом:

(5.12)

где k и l – координаты в двумерном частотном домене; m и n – координаты в двумерном пространственном домене.

На практике со второй половины прошлого века большинство расчетов в прямом и обратном преобразовании Фурье выполняется с помощью высокоэффективного метода "быстрого преобразования Фурье".

3.5. Графическое изображение дискретного преобразования Фурье

Для лучшего понимания ДПФ рассмотрим графическую иллюстрацию этого процесса, показанную на рис. 5.9. Для простоты проанализируем одномерный сигнал. На левой стороне рис. 5.9 представлены графики функций в пространственном домене и на правой стороне – в частотном домене.

Рис. 5.9. Графическая иллюстрация дискретного преобразования Фурье [4]

На рис. 5.9,А и 5.9,В показаны графики сигнала f(x) и его непрерывного преобразованием Фурье F(u). Процесс выборки, как это следует из уравнения (5.5), выполняется умножением f(x) на бесконечную импульсную последовательность с интервалом между импульсами равном Δx (рис. 5.9,С). Преобразование этой последовательности также является бесконечной последовательностью с частотным интервалом равном 1/(Δx) (рис. 5.9,D). Выборочная функция f(n·Δx) показана на рис. рис. 5.9,E.

Из теоремы свертки известно, что перемножение в одном домене эквивалентно свертке в другом домене. Таким образом, преобразование Фурье f(n·Δx) есть просто функция F(u) (рис. 5.9,B), свернутая с бесконечной последовательность импульсов (рис. 5.9,D). Как можно видеть из рис. рис. 5.9,F, выборка функции порождает репликацию ее преобразования Фурье с периодом 1/(2Δx), и дополнительно наблюдается небольшой эффект наложения, так как репликации более высоких частот имеет тенденцию свертки в частотный диапазон исходной трансформации F(u).

Согласно теореме свертки, если f(x) не имеет частотного ограничения (т.е. F(u) ≠ 0 для |u| > u_c), то возникнет погрешности наложения. Эффект наложения можно уменьшить с помощью сужения интервала выборки (Δx). Дискретная функция, показанная на рис. 5.9,Е, является бесконечно длинной последовательностью. Для представления в цифровом компьютере требуется конечное число выборочных значений. Таким образом, необходимо усечение или оконное представление бесконечной последовательности. Этот шаг очень существенен в процессе выборки и выражается графически через перемножение f(n·Δx) (рис. 5.9,Е) с прямоугольным импульсом шириной, равной полю обзора камеры FOV (рис. 5.9,G). Усеченная выборочная последовательность f(i) показана на рис. 12.6,I. Преобразование Фурье прямоугольного импульса представляет синусоидальну функцию 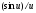(рис. 5.8,H).

Из теоремы свертки следует, что перемножение в пространственном домене эквивалентно свертке в частотном домене. Поэтому существенное усечение, которое было реализовано прямоугольным импульсом шириной, равной FOV, эквивалентно свертке выборочной частотной трансформанты с синусоидальней функцией, показанной на рис. 5.8,H. По этой причине частотная трансформация f(i) содержит небольшие пульсации, видимые на рис. 5.9.J. Дискретное преобразование Фурье выполняется выборкой функции, показанной на рис. 5.9.J, с интервалом выборки 1/ FOV в частотном диапазоне Этот анализ наглядно выявил два эффекта, которые вызывает дискретное преобразование Фурье в отличие от непрерывного преобразования Фурье, а именно, частотное наложение и усечение.