Лабораторная работа №2.1а «законы постоянного тока»

I. Цель работы: изучить и проверить экспериментально законы Ома и законы Кирхгофа; определить ЭДС источника и его внутреннее сопротивление.

Рисунок 1 – Общий вид блока «Электрические цепи» ЛКЭ-2

II. Описание установки.

Для выполнения работы используется блок «Электрические цепи» лабораторного комплекса ЛКЭ-2, внешний вид блока представлен на рис. 1. В состав блока входят наклонный каркас 1, модуль «Цепи постоянного тока» 2 и модуль «Цепи переменного тока» 3. Исследуемая лампа находится в правом нижнем углу модуля 2. На задней панели установки смонтированы цифровые мультиметры для измерения напряжения, тока и сопротивления (на рис. 1 не показаны).

III. Методика измерений и расчетные формулы.

З

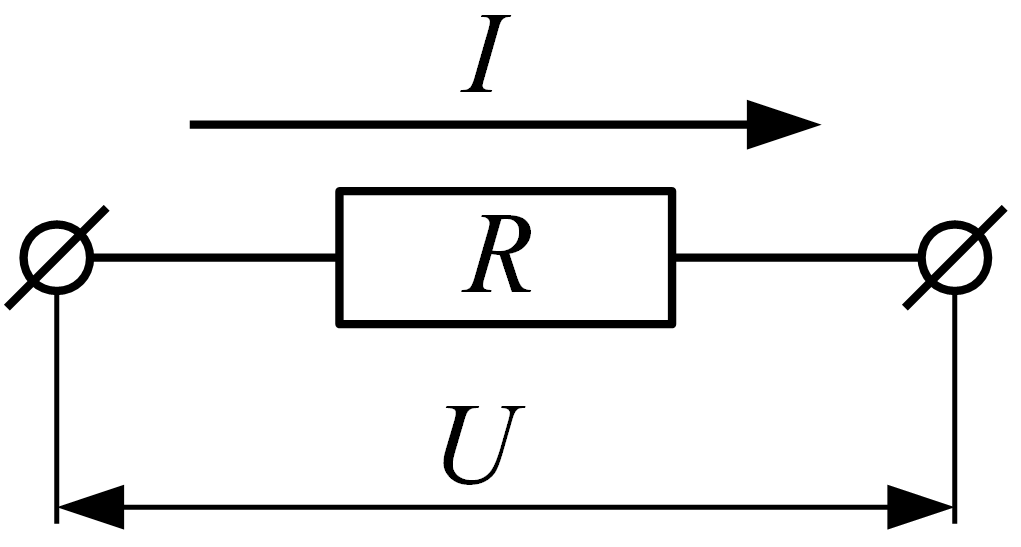Рисунок 2 – К закону Ома для участка цепи

акон Ома для участка цепи: сила тока I в участке цепи прямо пропорциональна напряжению U и обратно пропорциональна сопротивлению R (см. рис.2):

. (1)

З

Рисунок 3 – К закону Ома для замкнутой цепи

акон Ома для замкнутой цепи: сила тока I в замкнутой цепи пропорциональна ЭДС ε источника и обратно пропорциональна полному сопротивлению цепи (см. рис.3):

. (2)

Электродвижущая сила источника (ЭДС) создает разность потенциалов, которая перемещает заряды и создает ток. ЭДС источника численно равна работе сторонних сил по перемещению единичного заряда. Сторонние силы – это силы неэлектростатического происхождения (механические, химические, магнитные), которые производят разделение положительных и отрицательных зарядов. Внутри источника разноименные заряды движутся в разные стороны, создавая на одном контакте избыток электронов, на другом контакте – избыток положительных зарядов. Электростатические силы разделить заряды не могут, т.к. разноименные заряды притягиваются.

Н

Рисунок 4 – Узел электрической цепи

а практике часто приходится рассчитывать сложные разветвленные электрические цепи, содержащие узлы. Узел в разветвленной цепи – это точка, в которой сходятся не менее трех проводников (рис. 4). Ветвь – это участок цепи между двумя узлами. Для упрощения расчетов разветвленных цепей обычно используют законы Кирхгофа.

Первый закон Кирхгофа: алгебраическая сумма токов сходящихся в узле равна нулю:

. (3)

При этом ток, входящий в узел, считается положительным, а ток, выходящий из узла – отрицательным.

Второй закон Кирхгофа вытекает из обобщённого закона Ома для разветвлённых цепей: алгебраическая сумма произведений токов на сопротивления вдоль любого замкнутого контура равна алгебраической сумме ЭДС, действующих в этом контуре:

. (4)

При использовании законов Кирхгофа расчет разветвленной цепи постоянного тока следует производить по следующему алгоритму:

1. Произвольно выбрать направление обхода контура (по ходу часовой стрелки или против).

2. Произвольно выбрать и обозначить на схеме стрелками направление токов во всех ветвях, причем в пределах одной ветви ток должен иметь только одно значение и направление.

3. Произвольно выбрать замкнутые контуры так, чтобы каждый новый контур содержал хотя бы одну ветвь, не входящую в ранее рассмотренные контуры.

4. Если выбранное направление обхода контура совпадает с направлением тока I_j, то падение напряжения I_jR_j на соответствующей ветви берётся со знаком плюс, в противном случае – со знаком минус.

5. Перед ЭДС ℰ_i ставится знак плюс, если данная ЭДС повышает потенциал в направлении обхода (направление обхода проходит внутри источника от отрицательного полюса к положительному), в обратном случае ЭДС записывается со знаком минус.

6. Общее число уравнений по законам Кирхгофа равно числу различных токов в электрической цепи, причём число уравнений, составленных по первому закону Кирхгофа, на единицу меньше числа узлов.

В

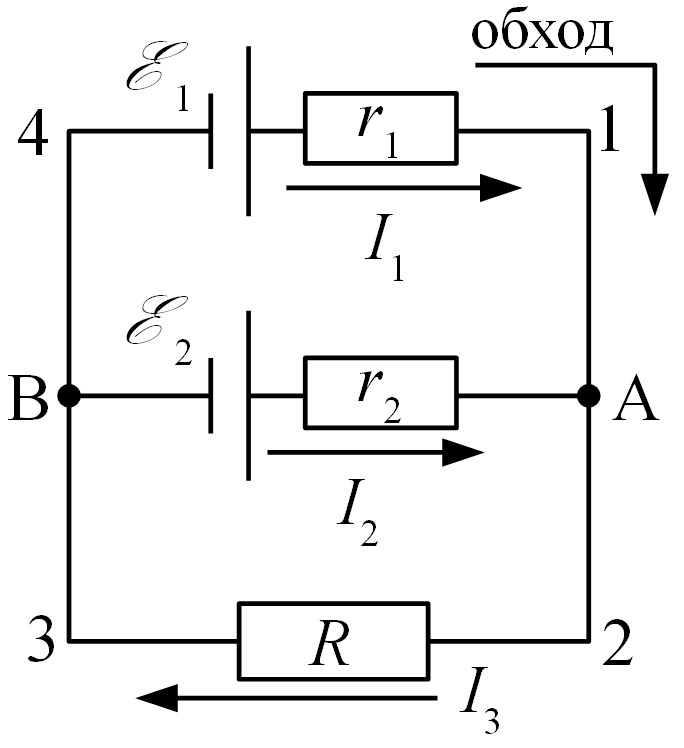Рисунок 5 – Пример разветвленной цепи

качестве примера рассмотрим цепь, изображенную на рис.5:

1. произвольно выбираем направление обхода, например, по часовой стрелке;

2. произвольно указываем направления токов в ветвях, при этом необходимо, чтобы в каждом узле часть токов втекала, а часть токов вытекала;

3. данная цепь содержит 2 узла: А и В. Уравнение первого закона Кирхгофа достаточно записать только для одного, т. к. уравнение для второго узла повторит уравнение для первого. В узле А имеем:

I₁ + I₂ – I₃ = 0; (5.1)

4. в данной цепи можно выделить 3 контура: 1-А-В-4-1, А-2-3-В-А, 1-А-2-3-В-4-1, причем последний является повторением двух предыдущих. Поэтому второй закон Кирхгофа достаточно записать для любых двух контуров:

для контура 1-А-В-4-1: ε₁ – ε₂ = I₁r₁ – I₂r₂; (5.2)

для контура 1-А-2-3-В-4-1: ε₁ = I₁r₁ + I₃R. (5.3)

Решая совместно уравнения (5.1), (5.2) и (5.3), можно рассчитать режим работы цепи, т. е. все токи и напряжения на элементах цепи.