1.3. Разрядка конденсатора

При замыкании выключателя К в положение 2, заряженный конденсатор С, обладающий энергией W = CU²/2, начинает разряжаться, т.е. в цепи появляется разрядный ток.

Согласно закону Ома мгновенное значение силы тока через сопротивление при разрядке конденсатора равно i=U_c/R.

Поскольку заряд конденсатора при разрядке уменьшается с течением времени, то i = -dq/dt.

Так как dq = CdU_c, то получим i = -CdU_c/dt. Отсюда dU_c/U_c = -dt/RC.

Интегрируя полученное выражение с учетом того, что при t=0, U_c = U, имеем:

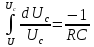
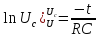
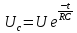
Следовательно, напряжение на конденсаторе при его разрядке уменьшается по экспоненциальному закону, а разрядный ток определяется по закону

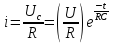(4)

На рис. 3 представлены графики зависимости U_c(t) и i(t) при разрядке конденсатора.

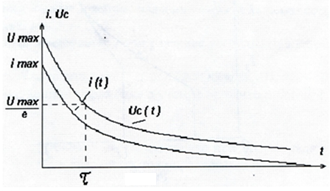
Рис. 3

В начальный момент времени разрядный ток имеет максимальное значение i_max=U/R. За время τ=RC разрядный ток уменьшается в e раз. Энергия, сосредоточенная в электрическом поле заряженного конденсатора, выделяется в виде тепла на сопротивлении R. Рассмотренные переходные процессы используются в радиотехнике, для измерения малых промежутков времени, для получения мощных электрических разрядов, в релаксационных генераторах (генераторах пилообразного напряжения).

Итак, в переходных процессах, происходящих при заряде и разряде конденсатора, ток и напряжение на конденсаторе с течением времени изменяется по экспоненциальному закону ().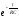

Произведение RС имеет размерность времени и называется постоянной времени или временем релаксации τ =RC. За время τ заряд конденсатора уменьшается в e раз.

Для определения RС часто удобно измерять время, за которое величина заряда или напряжения падает до половины первоначального значения, так называемое "половинное время" t_1/2. "Половинное время" определяется из выражения

,

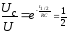Взяв натуральный логарифм от обеих частей уравнения, получаем 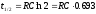, или

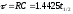₍₅₎

Способ измерения постоянной времени состоит в определении t_1/2 и умножении полученной величины на 1,44. Так как экспонента асимптотически приближается к оси абсцисс, то точно установить окончание процесса разряда конденсатора (так же как и процесса заряда) не представляется возможным. Поэтому целесообразно изме­рять время уменьшения величины напряжения в 2 раза, т.е. “половинное время”. За каждый интервал времени t_1/2=0,693ּRC заряд на емкости уменьшается в два раза (рис. 4).

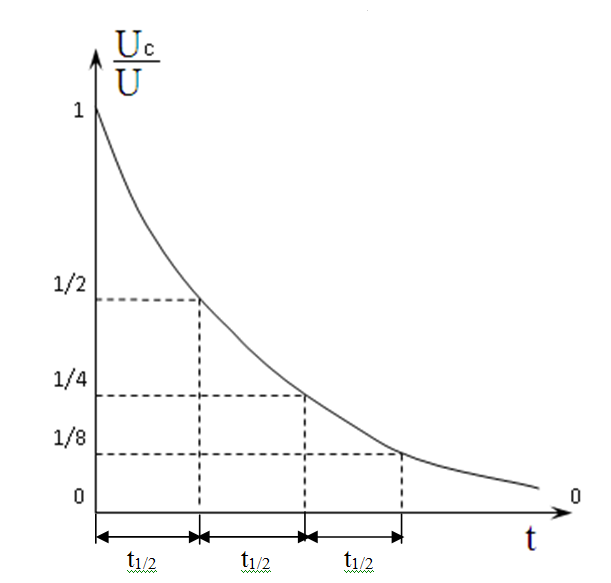
Рис. 4

Кроме того, постоянную времени можно найти графическим способом. Из формулы (4) находим:

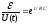, (6)

Логарифмируя левую и правую части формулы (11), получаем

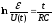. (7)

Построив логарифмическую зависимость, y=f(x), где 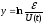, а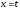, получим прямую, котангенс угла наклона которой к оси Х есть время релаксации , или постоянная времениRC:

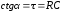. (8)

Если обкладки конденсатора попеременно подключать к источнику тока и к сопротивлению R (рис. 5), то график процесса заряд-разряд конденсатора будет иметь вид, показанный на рис. 6. Процесс заряда-разряда можно наблюдать с помощью осциллографа, подавая на вход Y напряжение с конденсатора C.

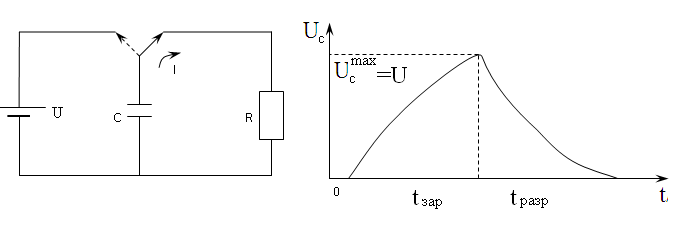
Рис. 5 Рис. 6