1) Вычислить значение z1 в точке в;

2) вычислить приближенное значение z₁ в точке В, исходя из значения z_o функции в точке А, заменив приращение функции при переходе от точки А к точке В дифференциалом; оценить в процентах, относительную погрешность, возникающую при замене приращения функции дифференциалом;

3) составить уравнение касательной плоскости и нормали к поверхности z = f(x,y) в точке С(х₀,у₀,z₀).

A(2;-1) B(2,02; -0,99)

A(-1;3) B(0,98; 2,97)

A(3;2) B(2,97; -2,02)

A(1;4) B(1,03; 4,01)

A(-1;-1) B(-0,97; -1,02)

A(4;-3) B(3,98; -3,03)

A(3;2) B(3,02; 1,98)

A(-2;5) B(-1,98; 5,01)

A(-2;3) B(-2,02; 2,97)

A(3;-4) B(3,04; -4,02)

331-340. Вычислить неопределенные интегралы. Ответы проверить дифференцированием.

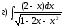
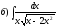
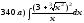
341-350. Вычислить определенный интеграл.

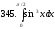
351-360. Найти определенный интеграл по формуле Ньютона-Лейбница.

361-370.Найти несобственный интеграл.

371-380. Вычислить несобственный интеграл или установить его расходимость.

381-390. Вычислить приближенно интеграл, используя формулу трапеции. Промежуточные вычисления выполнить с тремя значащими цифрами, а результат округлить до двух. Промежуток интегрирования разбить на 10 равных частей.

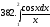
391-400. Найти площадь фигуры, ограниченной заданными линиями. Сделать чертеж.

401-410. Найти объем тела, образованный вращением вокруг оси Ох (Vx) или оси Оу (Vy) фигуры, ограниченной заданными линиями. Сделать чертеж.

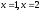
411-420. Вычислить площадь фигуры, ограниченной кривыми.

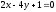
421-430. Решить дифференциальные уравнения первого порядка:

при х → ∞

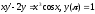
при х → ∞

при х → ∞

, у ограничено при х → ∞

при

при

431-440. Найти общее решение дифференциального уравнения 2-го порядка.

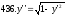
441-450. Найти частное решение дифференциального уравнения.

,

,

,

,

,

,

,

,

,

,

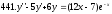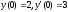
451-460. Решить задачу:

451. Найти такую кривую, проходящую через точку (0; -2), чтобы угловой коэффициент касательной в любой ее точке равнялся ординате этой точки, увеличенной в три раза.

452. Доказать, что кривая, угловой коэффициент карательной которой в любой точке пропорционален абсциссе точки касания, есть парабола.

453. Найти кривую, для которой угловой коэффициент касательной в какой-либо точке в nраз больше углового коэффициента прямой, соединяющей ту же точку с началом координат.

454. Найти кривую, обладающую тем свойством, что отрезок касательной к кривой, заключенный между осями координат, делится в точке касания пополам.

455. Определить кривую, у которой отношение отрезка, отсекаемого касательной на оси ОУ, к радиусу - вектору точки касания равно постоянной величине.

456. Найти кривую, обладающую тем свойством, что величина перпендикуляра, опущенного из начала координат на картельную, равна абсциссе точки касания.

457. Найти кривую, для которой длина отрезка, отсекаемого на оси ординат нормалью, проведенной в какой-нибудь точке кривой, равна расстоянию этой точки от начала координат.

458. Найти такую кривую, проходящую через точку (0, -2), чтобы тангенс угла наклона касательной в любой ее точке равнялся ординате этой точки, увеличенной на три единицы

459. Найти кривые, обладающие тем свойством, что отрезок, который касательная в любой точке кривой отсекает на оси ОУ, равен квадрату абсциссы точки касания.

460. Найти кривую, у которой отрезок, отсекаемый касательной на оси ординат, равен полусумме координат точки касания.

461-470. Изменить порядок интегрирования в двойном интеграле. Сделать чертеж области.

471-480. Найти объем тела, ограниченного поверхностями.

481-490. Вычислить криволинейный интеграл:

а) первого рода;

б) второго рода по заданной линии L.

481. a) dl по отрезку ОА прямой, где О(0;0), А(1;2)

б) L:

482. а) dl om m A(1;1) до m.B(2;4) по параболе

б) dy вдоль ломаной ОАВ, где О(0;0), А(2;0), В(4;5)

483. a)dl om m A(1;1) до m.B(2;) по линии

б) вдоль контура -ка АВС, где А(1;0), В(1;1), С(0;1) обходя против часовой стрелки.

484. а) dl om m . A(0;a) до m. B(a;0) вдоль линии

б) om m. A(-1;1) до m. B(1;1) вдоль линии

485. а) dl om m. O(0;0) до m. B(;1) вдоль линии

б) вдоль ветви эллипса

486. а) от т. А(0;1) до т. В(;0) вдоль линииy=cosx

б) вдоль ломаной АВС, где А(1;2), В(1;5), С(3;5)

487. а) от т. А(а;0) до т. В(0;а), L:

_б) от т.А (0;1) до т. В(-1;е) вдоль линии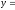

_{488. а)} вдоль первой арки циклоиды

б) вдоль отрезка АВ прямой, где А(1;2), В(2;4)

489. а) от т. А(0;0) до т. В(1;1) вдоль линии

_б) om m. O(0;0) до m.B(1;2) вдоль линии

_{490. а)}dl om m . A(0;1) до m. B(1;2) вдоль линии

_б) om m A(1;0) доm.B(е;1) вдоль линии y=lnx

491-500. Дан вектор , плоскости (р); х=0, у=0, t=0.

Найти: