2. Скп функции измеренных величин

Задача по установлению связи между СКП функции измеренных величин, ковариационная матрица которых оценена, и показателями точности и коррелированности её аргументов решена в курсе «ТВ и МС». Имея в своём распоряжении упомянутую формулу связи, мы можем решать две задачи: «прямую» и «обратную». В свою очередь, в рамках «прямой задачи» можно либо предвычислять СКП функции по предполагаемым (предписываемым) СКП аргументов σ_i и соответствующим ковариациям K_ij, либо оценивать СКП функции по полученным из результатов наблюдений оценкам СКП аргументов m_i и ковариаций K_ij. Прямая задача имеет частный случай, когда аргументы функции не коррелированны. В пределах этого ограничения и рассматривается «обратная задача» по предвычислению СКП стохастически не связанных аргументов по требуемой СКП их функции.

Прямая задача.

Дано:

z = f(x₁, x₂, …, x_n), (R.1)

дифференцируемая функция случайного вектора, аргументы которого получены по результатам измерений, характеризующимся некоторой оценкой ковариационной матрицы K_X вектора измерений X_1n^T = (x₁, x₂, …, x_n)

. (R.2)

Предполагается, что оценки дисперсий m_i² и корреляционных моментов «K_ij» найдены по данным соответствующих наблюдений по формулам

= , (R3)

где v =  x, n_i – объём наблюдений, выполненных для оценивания i-ой СВ, и

K_ij = 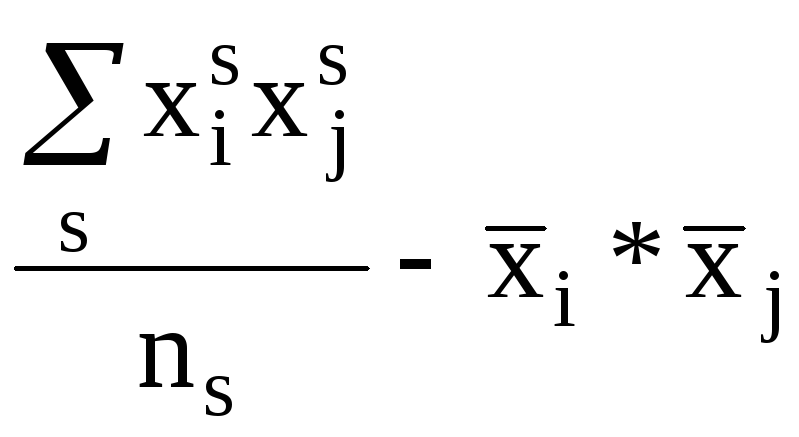. (R4)

Найти: m_Z  ?

Решение:

Опираясь на теорему о дисперсии дифференцируемой функции случайного вектора, мы считаем допустимым существование аналогичных связей между несмещёнными оценками этих же параметров:

. (R.5)

Когда аргументы случайного вектора измерений не коррелированы попарно, формула R.5 упрощается, теряя слагаемые второй суммы, содержащие нулевые множители K_ij=0, :

(R.6)

Обратная задача (для некоррелированных аргументов!).

Дано:

z = f(x₁, x₂, …, x_n) –

дифференцируемая функция СВ, аргументы которого не коррелированы,

а m_Z – СКП этой функции, которую необходимо гарантировать, организовав измерения X_1n^T = (x₁, x₂, …, x_n) с неизвестными СКП m_i.

Найти:

m_i – ? .

Решение:

Воспользуемся связью R.6: .

Одно уравнение R.6 содержит «n» неизвестных. Следовательно, оно имеет бесчисленное множество решений. Для выбора некоторого определённого варианта прибегают к дополнительным ограничениям, накладываемым на искомые неизвестные (СКП m_i).

1) Принцип равных СКП.

m_i = m_j = m (R.7)

Решая R.6 под условием R.7, получаем такой вариант ответа:

(R.8)

2) Принцип равных влияний.

(R.9)

Решая R.6 под условием R.9, получаем другой вариант:

(R.10)

3) Принцип имеющихся возможностей.

Пусть, кроме заданной СКП функции m_Z, мы имеем возможность измерить «k» аргументов с известными СКП m_i. Тогда, оставшиеся (n – k) аргументов m_j, можно определить, исходя из следующих преобразований:

(R.11)

. (R.12)

Далее, если , то задача решается либо по принципу равных СКП (R.8), либо по принципу равных влияний (R.10). Когда же , то имеющиеся возможности m_i не позволяют решить задачу, т.е. инструментальный парк, которым располагает исполнитель, не обеспечивает выполнение поставленной задачи. Отметим, что и в первом случае при , найденные СКП m_j могут оказаться слишком малыми величинами, не поддерживаемыми реальной аппаратурой.

3. Вес. Средняя квадратическая погрешность единицы веса.

Существует ещё один обобщённый показатель точности измерений, широко распространённый в геодезических и астрономических вычислениях. Он называется «вес» и представляет собой величину, обратно пропорциональную дисперсии:

P = c / ^. (P.1)

Коэффициент пропорциональности «с» – это дисперсия измерений, вес которой принимается равным единице, или, более кратко, дисперсия единицы веса (ДЕВ). Таким образом

с = . (Р.2)

Величина _ – это стандарт, с весом равным единице.

Практически мы всегда имеем дело не с дисперсиями, а с их оценками, квадратами СКП:

P = c / m^. (P.3)

с = μ² = (Р.4)

Положительное значение квадратного корня из коэффициента пропорциональности «с» называют «средней квадратической погрешностью (СКП) измерений, вес которых принят за единицу» или более лаконично – «СКП единицы веса».

Веса могут быть безразмерными, если мы имеем дело с однородными величинами. Когда же совокупность измерений – разнородный массив, то одна группа весов будет безразмерной, а другие – размерными, что необходимо учитывать как при выводе формул, так и при вычислениях.

Из формулы (Р.3) следует, что веса измерений, определяемые в едином масштабе «с», обратно пропорциональны квадратам соответствующих СКП:

. (Р.5)

Формула (Р.3), учитывающая введённое обозначение (Р.4), позволяет выразить СКП измерений «m» через СКП единицы веса «» и вес этих измерений «Р»:

m = *. (P.6)