Теория математической обработки геодезических измерений

1Теория погрешностей

1. Обработка и анализ измерений одной величины

   1. Моделирование погрешностей измерений

Пусть X – истинное значение измеряемой величины, остающееся неизменным в процессе измерений;

Х – случайная величина (СВ), представляющая собой вероятностную модель измерительной технологии;

x_i – значение величины X, представляющее собой результат i-го измерения и являющееся элементом спектра СВ «X», т.е. ;

i = 1, 2, ... , n – индекс измерения;

n – количество измерений;

E(X) – математическое ожидание (МО) СВ «X»;

– дисперсия СВ «X».

В такой ситуации можно определить следующие погрешности измерений:

_i = x_i – X – истинная погрешность i-го измерения; (Т.1)

_i = x_i – E(X) – случайная погрешность i-го измерения; (Т.2)

 = E(X) – X – постоянная погрешность технологии измерений. (Т.3)

Очевидно, что

_i = _i + , (Т.4)

т.е. истинная погрешность представляет собой сумму случайной и постоянной погрешностей.

Определения (Т.1) – (Т.4) иллюстрируются (Рис. Т.1) на совмещенных числовых осях X и  (индекс «i» опущен):

0    

| | | |

0 X E(X) x X

Рис. Т.1. Истинная, случайная и постоянная погрешности.

(Имеется только результат измерений «x» относительно известного начала 0.)

Представим основные числовые характеристики – математические ожидания (МО), дисперсии и начальные моменты второго порядка – каждого вида погрешностей, опираясь на определения (Т.1) – (Т.3) и известную связь между начальными и центральными моментами второго порядка (_ = σ² + ₁²):

Постоянная погрешность : E() = ; D() = 0; _() = ^.

Случайная погрешность : E() = 0; D() = ; _() = .

Истинная погрешность : E() = ; D() = ; _()= + ^.

Убедитесь в данных результатах в качестве Упражнения, помня что:

E() = ≡ 0; E(X) = , D(X) = , а _(X) = + ()².

Все приведённые числовые характеристики погрешностей связаны между собой так же, как и сами погрешности (Т.4):

E() = E() + E() =  (Т.5)

D() = D() + D() = (Т.6)

_() = _() + _() = + ^ (Т.7)

Постоянная погрешность , будучи детерминированной величиной, не является объектом вероятностного моделирования. Её значения определяют из специальных исследований, а в среднее арифметическое результатов измерений вводят соответствующую поправку. Это – один путь учета влияния постоянных погрешностей. Другой путь борьбы с ними заключается в надлежащей организации технологии измерений, компенсирующей эти погрешности в окончательных результатах x_i. Дело в том, что результат измерений x_i обычно является функцией нескольких отсчетов (операций), по которым он вычисляется. Например, углы при геодезических и астрономических измерениях определяют при альтернативных положениях вертикального круга и на разных участках лимба. Если результаты x_i не содержат постоянной погрешности, определяемой формулой (Т.3), т.е. = E(X) – X = 0, то

E(X) = X. (Т.8)

Выражение (Т.8) эквивалентно условию отсутствия постоянной погрешности в измерениях.

Специальные исследования, направленные на определение постоянной погрешности, могут представлять собой процедуру, подобную эталонированию. Эталон, согласно [РМГ 29–99] – это «средство измерений…, предназначенное для воспроизведения и (или) хранения единицы (физической величины) и передачи её размера … средствам измерений». Численно он представляет собой некоторую меру, значение которой известно с высокой степенью точности.

Обозначим числовое значение эталона как Y. Процедура эталонирования обычно заключается в измерении величины Y = const путём реализации некоторой технологии, вероятностная модель которой – это СВ «Y». В результате мы получаем выборку y₁, y₂, …, y _k. Пусть эта выборка простая, т.е. не коррелированная и равноточная. Полагая, что выборка принадлежит генеральной совокупности (ГС) «Y», она же СВ «Y», мы можем оценить её МО. В курсе ТВ и МС показано, что оптимальной оценкой МО ГС «Y» по данным простой выборки является среднее арифметическое, представляющее собой состоятельную и несмещённую оценивающую функцию (ОФ) с минимальной дисперсией:

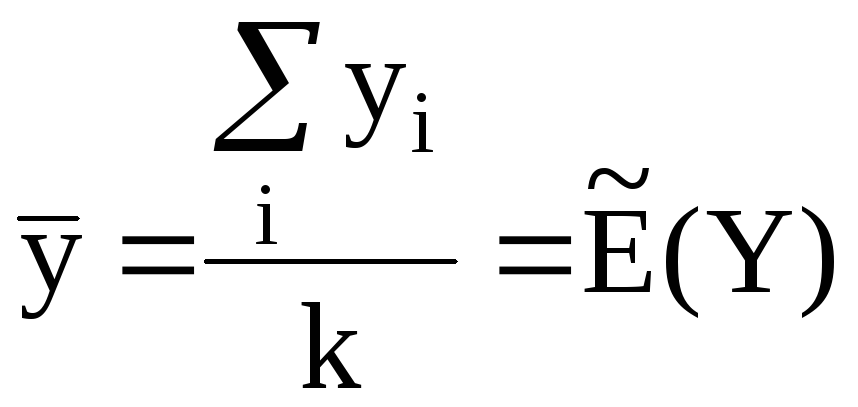. (Т.9)

Разность между оценкой (Т.9) и значением эталона Y позволит оценить постоянную погрешность:

– Y. (Т.10)

Естественно, что должна быть проверена нулевая гипотеза о незначимости найденной постоянной погрешности

H₀ = {E(Y) = Y } (Т.11)

против альтернативной

H_A = {E(Y) ≠ Y }. (Т.12)

Нулевая гипотеза (Т.11) проверяется с помощью теста

t_Э = (–Y) / . (Т.13)

Здесь

, а 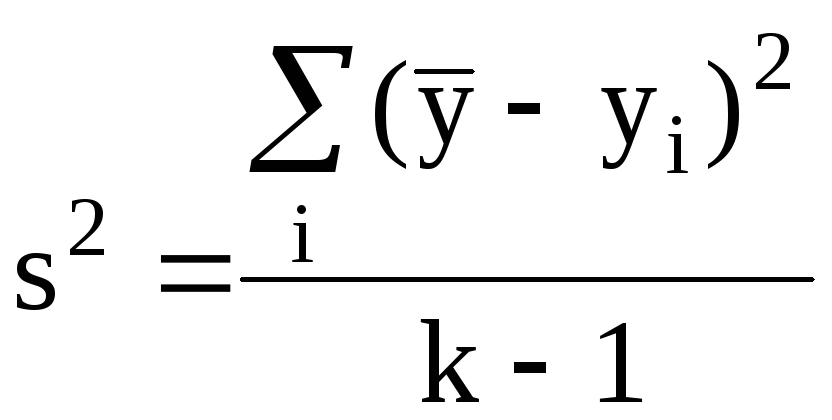. (Т.14)

Критическая область проверяемой гипотезы находится за пределами интервала t_T = [t_H; t_B]. Нижняя t_H и верхняя t_B границы интервала – это квантили распределения Стьюдента, определяемые при (k – 1) степенях свободы на уровне значимости :

t _H = t _{k-1;1-}t_B = t _{k-1;}t_H

Когда t_Э t_T, нулевая гипотеза отвергается, т.е. постоянная ошибка δ_Э признаётся значимой, то она должна вводиться в каждый очередной результат , с целью нахождения наиболее надёжного значения (ННЗ) X измеряемой величины X:

X = – δ_Э. (Т.15)

В случае незначимости постоянной погрешности _Э, ННЗ X величины X принимается равным СА . В такой ситуации истинная  и случайная  погрешности совпадают: .

Далее обратимся к случайным погрешностям  и определим их основные свойства, полагая распределение этих погрешностей нормальным. Данное предположение основывается на том, что технологии геодезических измерений соответствуют условиям «Центральной предельной теоремы».

Нормальное распределение СВ «X» характеризуется двумя параметрами: a= E(X) и b = _X. Для случайной погрешности  = x – E(X) они будут равны следующим значениям:

a_Δ = E() = 0 и b_Δ = _Δ = _X. Тогда плотность нормальной случайной погрешности будет иметь вид:

f() =e ^. (Т.16)

Этой функции соответствует следующий график (рис.Т.2):

f(X) f()

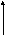
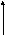P(> 0) = P( 0)

0 

0 E(X) X

Рис. Т.2. Плотность распределения нормальной случайной погрешности.

Нормальную случайную погрешность  можно стандартизировать и перейти к стандартному значению t случайной погрешности, вычисляемому по формуле:

t = _X. (Т.17)

Уравнение плотности (Т.16) определяет, а Рис. Т.2 иллюстрирует основные свойства случайных погрешностей, распределенных по нормальному закону.

1. Случайные погрешности имеют нулевое МО (При любом законе распределения!):

E() = 0. (Т.18)

2. Положительные и отрицательные случайные погрешности равновероятны (Для симметричных распределений!):

P(> 0) = P( 0) = 1/2. (Т.19)

3. Малые по абсолютной величине случайные погрешности более вероятны, чем большие, т.е.:

P(0 < || < _X) 0.68 > P(_X < || <_X) 0.27. (Т.20)

В последней формуле (Т.20) конкретные значения вероятностей 0,68 и 0,27 как раз и соответствуют нормальному распределению.

Наиболее распространённым и удобным обобщённым показателем точности или неопределённостью случайных погрешностей измерений чаще всего служит их средняя квадратическая погрешность (СКП) измерений, представляющая собой оценку стандарта измерений, который одновременно является стандартом случайных погрешностей:

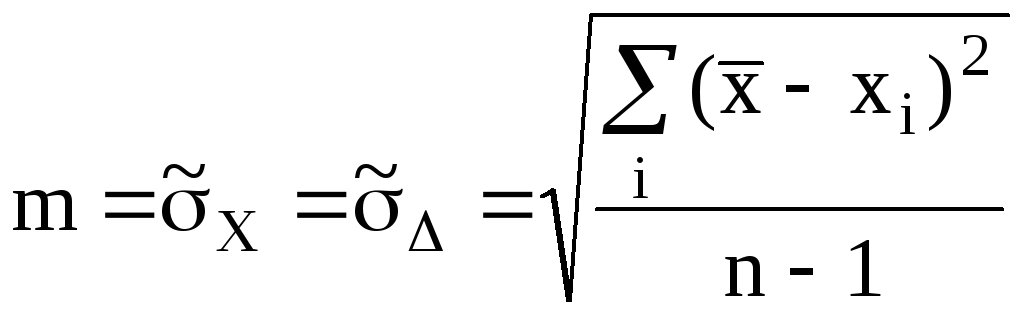. (Т.21)

Дополнительными показателями точности измерений, т.е. точности случайных погрешностей служат ещё две величины: средняя погрешность ϑ_X=[||] / n или ϑ_X =[|v|] / (n – 0,5), как оценка среднего отклонения, и срединная погрешность ρ=|_n| или ρ=|v_n|, как оценка срединного отклонения. При нормальном распределении случайных погрешностей между этими показателями и средней квадратической погрешностью существует функциональная зависимость:

ϑ_X ≈ 0,8 m или m ≈ 1,25 ϑ_X; (Т.22)

ρ ≈ ⅔ m или m ≈ 1,5 ρ. (Т.23)

Приведённые соотношения могут служить «быстрыми» критериями проверки гипотезы о нормальности распределения. Однако их мощность много ниже критериев Пирсона или Колмогорова-Смирнова. В связи со сказанным, было бы уместно рассматривать эти соотношения в качестве индикаторов нормальности.