2.6.3. Работа с таблицами стандартного нормального рас­пределения

Для практического применения приведенных выше распределений к проведению статистических расчетов служат таблицы распределений. Обычно табулируется функция распределения стандартного нормального распределения на интервале (-, +)или на интервале [0; +). Рассмотрим использование таблицы функции распределения стандартного нормального распределения на интервале (-, +). Таблица имеет вид

z	0	1	2	3	4	5	6	7	8	9
0	0,500	0,504	0,508	0,512	0,516	0,520	0,524	0,528	0,532	0,536
0,1	0,540	0,544	0,548	0,552	0,556	0,560	0,564	0,567	0,571	0,575
…	…	…	…	…	…	…	…	…	…	…
4	1,000	1,000	1,000	1,000	1,000	1,000	1,000	1,000	1,000	1,000

В приведенном фрагменте таблицы значения функции распределения приведены с точностью до пятого десятичного знака, а значения аргумента z- до второго десятичного знака. В самом левом столбце таблицы приведены значенияzот 0,0 до 4,0 с точностью до десятых долей, а в верхней строке таблицы приведены сотые долиz. Значение функции распределения, соответствующее определенному значению аргументаz(например, 0,14), находится на пересечении строки с десятыми долямиz(в данном примере - 0,1) и столбца с сотыми долямиz(в данном примере - 4). В рассматриваемом примере оно равно 0,55567 и означает вероятность попадания случайной величиныzв полубесконечный интервал (-, 0,14). Эта вероятность равна 0,5 приz= 0, так как это значение делит область изменения случайной величиныг.на две равновероятные части, и стремится к единице при увеличенииz. Для того, чтобы рассчитать вероятность попадания величиныz в конечный интервал<z<, следует воспользоваться формулой:Prob{ < Z <}=F()-F(). Пусть, к примеру,=0,1, а= 0,14. Тогда по таблице находимF(0,1) = 0,53983, аF(0,14) = 0,55567. Следовательно, искомая вероятность попадания величиныzв интервал [0,1; 0,14) равнаF(0,14) -F(0,1) = 0,55567 - 0,53983 = 0,01584.

Вспоминая, что стандартная нормальная величина zсвязана с исходной случайной величинойхсоотношениемz= , мы можем определить вероятность попадания произвольной нормально распределенной величины х в интервал a < x < b как вероятность попадания стандартной нормальной величины z в интервал<z<. Определяя последний интервал, мы можем рассчитать искомую вероятность с помощью таблиц так же, как в рассмотрен­ном выше примере.

Рис. 2.3. Функции f(z), F(z), Ф(z) стандартного нормального рас­пределения

Отметим, что иногда в таблицах стандартного нормального распределения приведена не функция распределения, а величина

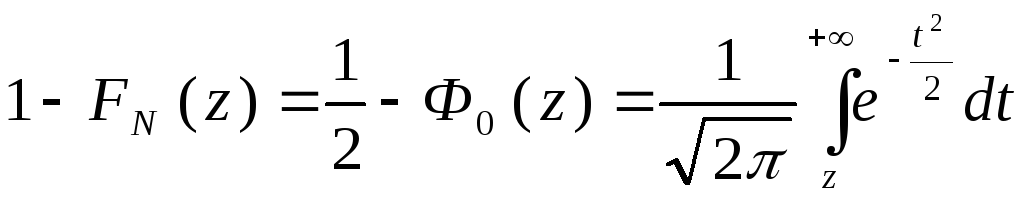, определяющая вероятность попадания случайной величиныZв среднюю часть функции распределения (интервал [0,z)) и изменяющаяся от 0 до 0,5 при измененииzот 0 до +иливеличина ,определяющая вероятность попадания случайной величиныZв правый"хвост" распределения (интервал [z, +)) и изменяющаяся от 0,5 до 0 при измененииzот 0 до +. Связь между собой трех вышеупомянутых функций показана на рис. 2.5.

Для всех этих функций вероятность попадания случайной величины Z взаданный интервал рассчитывается как разность значений соответствующих функций на концах этого интервала.