ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ – ВЫСШАЯ ШКОЛА ЭКОНОМИКИ

ПЕРМСКИЙ ФИЛИАЛ

Кафедра маркетинга и логистики

Булдакова Татьяна Анатольевна

ФИНАНСОВАЯ МАТЕМАТИКА

Учебно-методический комплекс

Пермь 2009

СОДЕРЖАНИЕ

Программа учебной дисциплины Вступительное слово к дисциплине

Глава 1. Общие понятия

1.1.Сущность финансовой математики

1.2.Простейшие сведения о процентах

1.3.Основные понятия, используемые в финансово-экономических расчетах

1.4.Вопросы и задачи для проверки усвоения пройденного материала

Глава 2. Операции наращения

2.1.Простые проценты

2.2.Английская, немецкая и французская практика начисления

2.3.Переменные ставки

2.4.Сложные проценты

2.5.Внутригодовые процентные начисления

2.6.Вопросы и задачи для проверки усвоения пройденного материала

Глава 3. Операции дисконтирования

3.1.Сущность дисконтирования

3.2.Математическое дисконтирование

3.3.Банковский учет

3.4.Ломбардный кредит

3.5.Вопросы и задачи для проверки усвоения пройденного материала

Глава 4. Потоки платежей и финансовые ренты

4.1.Потребительский кредит

4.2.Погашение ссуд одинаковыми платежами, на которые начисляются процентные деньги

4.3.Погашение ссуд одинаковыми платежами в случае, когда процентные деньги погашаются в зависимости от остатка долга

4.4.Погашение ссуд платежами, содержащими одинаковые выплаты долга, в случае, когда процентные деньги погашаются в зависимости от остатка долга

4.5.Погашение ссуд выплатами, изменяющимися в арифметической прогрессии, в случае, когда процентные деньги погашаются в зависимости от остатка долга

4.6.Погашение ссуд выплатами, изменяющимися в геометрической прогрессии, в случае, когда процентные деньги погашаются в зависимости от остатка долга

4.7.Погашение ссуд аннуитетами, последний из которых может отличаться от остальных, в случае, когда процентные деньги погашаются в зависимости от остатка долга

4.8.Постоянные финансовые ренты

4.8.1.Формулы наращенной суммы. Обычная годовая рента

4.8.2.Формулы современной величины. Обычная годовая рента

4.8.3.Зависимость между современной величиной и наращенной суммой ренты

4.8.4.Определение параметров финансовой ренты

4.9.Вопросы и задачи для проверки усвоения пройденного материала

5.Приложения

2

Методические рекомендации по написанию контрольной работы Контрольные работы Методические рекомендации по написанию зачетной работы

3

РАБОЧАЯ ПРОГРАММА УЧЕБНОЙ ДИСЦИПЛИНЫ

«ФИНАНСОВАЯ МАТЕМАТИКА»

1.ОБЯЗАТЕЛЬНЫЙ МИНИМУМ СОДЕРЖАНИЯ ДИСЦИПЛИНЫ ПО ГОС ВПО

2.ПОЯСНИТЕЛЬНАЯ ЗАПИСКА

1.Автор программы: старший преподаватель Татьяна Анатольевна Булдакова.

2.Требования к слушателям: Дисциплина "Финансовая математика" базируется на знаниях и умениях, полученных слушателями в ходе изучения математических и экономических дисциплин. Также, приступая к изучению данного курса для проведения финансовых вычислений, слушатель должен иметь первоначальные пользовательские навыки работы на калькуляторе и на персональном компьютере (ПК).

Аннотация: Данный курс является базовым и обеспечивает успешное изучение дисциплин цикла, связанного с экономическим анализом и экономико-математическим моделированием микроуровневых финансовых ситуаций. Основные виды занятий – это лекции и практические занятия. На лекциях рассматриваются наиболее важные модели решения типовых задач количественного анализа эффективности финансовых потоков и финансовых инструментов, поясняется логика финансовых операций, вводится терминология, наиболее устоявшаяся на сегодняшний день, проводится математический анализ процентных ставок и доходов с актива, исследуются дискретные и непрерывные схемы начисления процентов, используемые для оценки денежных потоков, анализируются новые финансовые инструменты. На практические занятия в качестве основных учебных вопросов выносится решение типовых задач финансового анализа и отработка навыков финансовых вычислений.

3.Учебная задача курса:

Врезультате изучения курса слушатель должен:

•знать логику финансовых операций в рыночной экономике;

•уметь применять и рассчитывать модели операций дисконтирования, модели финансовых потоков; модели инфляции; модели операций с финансовыми инструментами.

•иметь представление о целесообразности и возможности применения различных процентных ставок;

•обладать навыками работы с современными программами, позволяющими выполнять финансовые расчеты.

4.Формы контроля:

•текущий контроль заключается в написании контрольной работы.

•заключительный контроль - написание зачетной работы.

3.СОДЕРЖАНИЕ ПРОГРАММЫ

1.Основные понятия финансовой математики. Проценты, процентная ставка, первоначальная и наращенная суммы, период начисления, интервал начисления, декурсивный и антисипативный способы начисления процентов, процент, учетная ставка, простые и сложные проценты.

2.Простые ставки процентов. Нахождение наращенной суммы. Математическое дисконтирование. Случай изменения простой ставки процента.

3.Английская, немецкая и французская практики начисления процентов.

4

4.Простые учетные ставки. Дисконт. Банковский учет.

5.Сложные ставки процентов. Нахождение наращенной суммы. Математическое дисконтирование. Случай, когда период начисления не является целым числом. Случай изменения сложной ставки процента.

6.Начисление сложных процентов несколько раз в году. Номинальная процентная ставка. Эффективная процентная ставка.

7.Сложные учетные ставки.

8.Сравнение операций. Эквивалентные процентные ставки. Нахождение эквивалентной простой процентной ставки для простой учетной ставки.

9.Нахождение эквивалентной простой процентной ставки для сложной процентной ставки.

10.Нахождение эквивалентной простой процентной ставки для номинальной ставки сложных процентов.

11.Нахождение эквивалентной номинальной ставки сложных процентов для сложной процентной ставки.

12.Модели финансовых потоков. Основные понятия: аннуитет (финансовая рента), величина отдельного платежа, срок ренты, интервал ренты, постоянная и переменная ренты, ренты постнумерандо и пренумерандо, процентная ставка. Наращенная (будущая) сумма ренты, современная (приведенная) стоимость ренты.

13.Нахождение наращенной сумму.

14.Определение современной стоимости для простой ренты.

15.Определение срока простой ренты.

16.Определение процентный ставки для простой ренты.

17.Потребительский кредит. Его особенности.

18.Ломбардный кредит. Расчет ломбардного кредита.

19.Различные планы погашения долга.

4. УЧЕБНО-МЕТОДИЧЕСКОЕ ОБЕСПЕЧЕНИЕ ДИСЦИПЛИНЫ

Список литературы Основная:

1. Четыркин Е.М. Финансовая математика. -М.:Финансы и статистика, 2000.

Вспомогательная:

1.Финансовая математика: математическое моделирование финансовых операций. Учебное пособие под редакцией В.А. Половникова и А.И. Пилипенко.

2.К.А. Самаров, Финансовая математика, практический курс (учебное пособие).

3.В.И. Малыхин, Финансовая математика.

4.Г.И. Просветов, Математика в экономике (задачи и решения).

5

5. ТЕМАТИЧЕСКИЙ РАСЧЕТ ЧАСОВ

ТЕОРЕТИЧЕСКИЙ МАТЕРИАЛ ПО ДИСЦИПЛИНЕ

(учебное пособие)

Глава 1. ОБЩИЕ ПОНЯТИЯ

1.1.Сущность финансовой математики

С возникновение денег появились и финансовые вычисления, которые со временем превратились в самостоятельную дисциплину – Финансовую математику. Финансовая математика в широком смысле слова – это любые финансовые вычисления для достижения какой-либо цели. Очень часто приходится решать задачи, формально относящиеся к области финансовой математики. Коммерческие и финансовые вычисления сопровождают нас постоянно. В каком банке хранить деньги? Какой вид вклада лучше выбрать? Положить ли деньги в банк или закупить товары в прок? Обменять ли деньги на иностранную валюту или положить их в банк? Ехать ли за товарами на оптовый рынок или покупать их в ближайшем магазине? Подобные вопросы постоянно возникают у людей.

Чем больше у человека денег, тем шире круг финансовых проблем, стоящих перед ним. Выбор наилучших финансовых решений особенно важен для руководителей предприятий и людей, занимающихся индивидуальным предпринимательской деятельностью. С развитием денежного обращения совершенствовались и финансовые вычисления, она стали необходимыми для любой коммерческой деятельности.

Вместе с современными методами анализа и моделирования финансовых ситуации финансовые вычисления переросли в новое, более влиятельное направление организации и управления предпринимательской деятельностью – финансовый менеджмент. Но ядром финансового менеджмента остается всё же финансовая математика. В финансовой математике речь идет, прежде всего, об аппарате и методах расчетов, необходимых при финансовых операциях, когда оговариваются значения трех параметров: стоимостные характеристики (размеры платежей, кредитов, долговых обязательств), временные данные (даты и сроки выплат, отсрочки платежей, продолжительность

6

льготных периодов), специфические элементы (процентные и учетные ставки). Все эти параметры равноправны, игнорирование какого-либо одного из них может привести к нежелательным финансовым последствиям для одной из участвующих сторон.

Финансовая математика имеет и сугубо практическое значение. Она применяется в банковском и сберегательном деле, страховании, в работе финансовых организации, торговых фирмах, фондовых и валютных бирж, во внешнеэкономической деятельности. Но не следует полагать, что с помощью финансовой математики решаются все проблемы, с которыми сталкиваются в финан- сово-банковской практике. Финансовая математики – это всего лишь скелет науки о финансах, «нарастить мясо» на этом скелете – дело специальных дисциплин и кафедр.

В последние годы в России появилось много хороших книг отечественных авторов по классической финансовой математике, т.е. финансовой математике в условиях определенности. В первую очередь здесь необходимо отметить фундаментальные труды Е.М. Четыркина, В.И. Малыхина, Я.С. Мелкумова, В.В. Ковалева, В.А. Уланова и других исследователей.

Однако изучение книг по финансовой математике не является простым занятием для неподготовленного читателя. Еще более сложно, как выясняется, применять полученные теоретические знания на практике. Даже такое первоначальное понятие, как «процент», которое многим представляется совершенно прозрачным, на деле оказывается совсем не очевидным.

Проценты и являются отправной точкой, с которой начинается учебное пособие. Изложение всего материала проводится на примерах и задачах, имеющих максимально приближенный к реальности характер.

Таким образом, курс финансовая математика включает в себя следующие вопросы:

−общее понятие финансовой математики;

−исчисление будущей суммы денежных средств, находящихся во вкладах, займах или ценных бумагах при начислении процентов:

−учетный вексель;

−потребительский и ломбардный кредиты;

−определение параметров сделки;

−операции наращения и дисконтирования;

−потоки платежей и финансовые ренты;

−различные вопросы предоставления и возврата кредитов.

1.2.Простейшие сведения о процентах

Определение. Одну сотую долю числа α называют одним процентом числа α ; k сотых долей числа α называют k процентами числа α ; число α называют базой для нахождения про-

Пример 1. Даны два числа a и b. Сколько процентов составляет число b от числа a? Решение. Заметим, что в примере 1 базой для нахождения процентов является число a, и

предположим, что число b, составляет х % от числа a. По формуле (1.1)

b = 100x a ,

откуда вытекает

7

= 100b

x (1.2) a

Ответ. Число b составляет 100a b % числа a.

Задача 1.

Число a увеличилось в 3,7 раза. На сколько процентов увеличилось число a?

Пример 2. число уменьшилось в 2,5 раза. На сколько процентов уменьшилось это число? Решение. Обозначим рассматриваемое число буквой a. При уменьшении числа в 2,5 раза

(т.е. делении на 2,5) число a уменьшается на число b, причем

Ответ. Число a уменьшилось на 60 %.

Задача 2. Число увеличилось на 5 %. Во сколько раз увеличилось это число?

Пример 3. Налог на добавленную стоимость (НДС) равняется 18 % цены товара. Найти цену товара, если товар с учетом НДС стоит 1652 руб.

Решение. Обозначим через a цену товара без учета НДС. Стоимость товара с учетом НДС составляет 100% +18%=118% от a. Следовательно,

a*1,18=1652,

a = 16521,18 =1400 (руб.)

Ответ. Цена товара без учета НДС равна 1400 руб.

Пример 4. В течение первого месяца цена товара увеличилась на 30 %, а в течение следующего месяца новая цена товара уменьшилась на 10 %. На сколько процентов изменилась первоначальная цена товара за 2 месяца?

Решение. Обозначим через a первоначальную цену товара. Поступая, как при решении задачи 2 получаем, что по истечении первого месяца цена товара стала равной 1,3a. По условию задачи, за второй месяц новая цена товара, равная 1,3a (база), уменьшилась на 10 % и стала равной

1,3*a*0,9=1,17a.

Ответ. Первоначальная цена товара за 2 месяца увеличилась на 17 %.

Задача 3. В течение месяца цена товара увеличилась на 25 %, а в течение следующего месяца цена товара возвратилась к первоначальному уровню. На сколько процентов уменьшилась новая цена товара?

Пример 5. Банковский вклад, не тронутый в течение года, в конце этого года увеличивается на 10 %. На сколько процентов увеличится вклад, не тронутый в течение трех лет?

8

Решение. Обозначим через a первоначальную сумму вклада. Действуя, как при решении задачи 2, получаем, что по истечении первого года вклад станет равным 1,1a. По истечении второго года вклад станет равным 1,1*a*1,1=1,21a, а по истечении третьего года 1,21*a*1,1=1,331a. Таким образом, вклад, не тронутый в течение трех лет, увеличивается на число b, равное 0,331a. В соответствии с формулой (1.2) первоначальная сумма вклада увеличивается на

Ответ. Вклад увеличится на 33,1 %.

Определение. Месячным темпом инфляции называется такое количество процентов, на которое возрастают цены товаров за месяц по сравнению с предыдущим месяцем.

Пример 6. Месячный темп инфляции равен 5 %. На сколько процентов возрастают цены за

год?

Решение. Обозначим через с цену товара в первый день года. Действуя, как при решении задачи 2, получаем, что через месяц после начала года цена товара будет равна 1,05с. Через два месяца после начала года цена товара составит

1,05*с*1,05=1,052с.

Еще через месяц (т.е. через три месяца после начала года) цена товара достигнет

1,052*1,05с=1,053с,

и т.д. Таким образом, через n месяцев после начала года цена товара станет равной

1,05nс, (1.3)

где n =1, 2, …, 12. Проводя для n = 12 вычисления на калькуляторе, по формуле (1.3) полу-

чаем

1,0512с=1,7959с.

Следовательно, с начала года цена товара с увеличилась на число 0,7959с, т.е. на 79,59 %. Ответ. При месячной инфляции 5 % цены вырастают за год на 79,59 %.

1.3.Основные понятия, используемые в финансово-экономических расчетах

В финансовой математике широко представлены все виды статистических показателей: абсолютные, относительные и средние величины.

Процентные деньги или просто проценты в финансовых расчета представляют собой абсолютные величины дохода (приращение денег) от представления денег в долг в любой его форме (при чем эта финансовая операция реально может и не состояться):

−выдача денежной ссуды;

−продажа в кредит;

−депозитный счет;

−учет векселей;

−покупка облигаций, ценных бумаг и т.п.

Таким образом, можно рассмотреть как абсолютную «цену долга», которую уплачивают за пользование денежных средств.

Обозначают процентные деньги латинской буквой I.

9

Процентная ставка – это величина, которая характеризует интенсивность начисления процентов. Процентная ставка обозначается через r и является относительным показателем.

Методика расчета проста: отношение суммы процентных денег, выплачивающихся за определенный период времени, к величине ссуды. Этот показатель выражается либо в долях единицы, либо в процентах. Таким образом процентная ставка показывает, сколько денежных единиц должен заплатить заёмщик (лицо, берущее деньги в долг) за пользование в течение определенного периода времени 100 единицам первоначальной суммы долга.

Исходную инвестированную сумму будем называть первоначальной суммой или современ-

ной (текущей) стоимостью, и обозначать PV (present value).

Наращенной суммой или будущей стоимостью будем называть первоначальную сумму долга с начисленными на неё процентами к концу срока ссуды и обозначать FV (future value), т.е.

FV=PV+I.

Коэффициент наращения или индекс роста показывает, во сколько раз выросла первоначальная сумма за время t, т.е.

Bt = FVPV .

Коэффициент Bt показывает, во сколько раз наращенная сумму FV больше первоначальной суммы долга PV, т.е. по существу является относительным показателем.

Обратным показателем к индексу роста является величина, называемая дисконт фактором Dt, который показывает, какую часть суммы PV составляет в сумме FV, т.е.

Dt = PVFV .

Отношение процентных денег к деньгам, возвращенным заемщиком кредитору (лицо, дающее деньги в долг), называют учетной ставкой и обозначают d, таким образом

d = FV − PV . FV

Между величинами d, r, Bt, Dt существует непосредственная связь, зная один из показателей можно вычислить и все другие показатели.

Период начисления – это промежуток времени, за который начисляются проценты. Интервал начисления – это минимальный промежуток времени, по прошествии которого

происходит начисления процентов.

Например, первоначальная сумма может быть инвестирована на 2 года (это период начисления), а проценты начисляться на нее будут каждый квартал (интервал начисления).

Различают 2 способа начисления процентных денег: декурсивный и антисипативный. При декурсивном способе проценты начисляются в конце каждого интервала начисления, и

при этом процентные деньги начисляются по ставке процентов r.

При антисипативном (предварительном) способе проценты начисляются в начале каждого интервала начисления, т.е. процентные деньги начисляются по учетной ставке d.

В обоих способах процентные ставки могут быть либо простыми (в течение всего периода начисления применяются к первоначальной сумме), либо сложные (в каждом интервале начисления применяются к текущей наращенной сумме).

1.4.Вопросы и задачи для проверки усвоения пройденного материала

10

1.Что такое проценты?

2.Что называется в финансовых расчетах процентом?

3.Что такое процентная, учетная ставка? Какая связь между ними существует?

4.Что такое процесс наращения?

5.Дать определение коэффициента наращения, индекса роста.

6.Какие существуют способы начисления процентных денег?

7.Уставной капитал компании «АВС» сформирован следующим способом: Алексей внес - 55 % того, что Василий и Семён – 80 % того, что Алексей и Василий вместе. Семён внес на 6900 руб. больше Алексея. Найти вклад Василия в уставной капитал.

8.Если из числа вычесть 120, то оно уменьшится на 20 %. Если к новому числу прибавить 60, то новое число возрастет на сколько процентов?

9.После двух повышений на одно и то же число процентов зарплата выросла на 44 %. На сколько процентов каждый раз она повышалась?

10.Из прибыли в 5 млн. руб. фирма отчисляет 49 % в строительный фонд, причем 4 % из них для строительства базы отдыха. Сколько денег из прибыли выделяет фирма для строительства базы отдыха?

Глава 2. ОПЕРАЦИИ НАРАЩЕНИЯ

2.1.Простые проценты

Рассмотрим процесс наращения, т.е. определения денежной суммы в будущем, исходя из заданной суммы сейчас. Экономический смысл операции наращения состоит в определении величины той суммы, которой будет или желает располагать инвестор по окончании этой операции. Здесь идет увеличение денежного потока от настоящего к будущему.

Величина FV показывает будущую стоимость первоначальной, «сегодняшней» величины PV при заданном уровне начисления процентов r.

Рис. 1. Экономический смысл операции наращения.

При использовании простых ставок процентов проценты (процентные деньги) определяются исходя от первоначально суммы долга.

Схема простых процентов предполагает неизменность базы, с которой происходит начисление процентов.

Из определения процентов не трудно заметить, что процентные деньги представляют собой абсолютные приросты.

I=FV-PV, а поскольку база для их начисления является постоянной, то за n лет общий абсолютный прирост составит:

11

где по определению процентной ставки

r = FV − PV PV

Таким образом, размер ожидаемого дохода FV зависит от трех факторов: от величины инвестированной суммы PV, от уровня процентной ставки r, от срока финансовой операции n (в годах). Тогда наращенную сумму по схеме простых процентов можно будет определить по формуле:

FV = PV+I = PV + r*PV*n = PV*(1+r*n) – формула простых процентов.

Пример 1. Первоначальная сумма PV = 5000 руб. помещена в банк на n = 2 года под r = 15 % годовых (проценты простые). Тогда наращенная сумма после двух лет составит:

FV = PV*(1+r*n)=5000*(1+0,15*2)=6500 руб.

Пример 2. Сумма в размере 2000 руб.дана в долг на 2 года по схеме простых процентов под 10 % годовых. Определить проценты и сумму, подлежащую возврату.

Решение: Сумма подлежащая возврату: FV = PV*(1+r*n)=2000*(1+0,1*2)=2400 руб. Сумма начисленных процентов:

I=FV-PV=2400-2000=400 руб. или I=PV*r*n=2000*0,1*2=400 руб.

Таким образом, через два года необходимо вернуть общую сумму в размере 2400 руб., из которой 2000 руб. составляет долг, а 400 руб. – процентные деньги или «цена долга».

Задача 1. Первоначальная сумма PV = 7000 руб. помещена в банк на r = 3 года под r = 18 % годовых (простые проценты). Найти наращенную сумму.

Зная первоначальную сумму PV, наращенную сумму FV , простую годовую процентную

Пример 3. Первоначальная сумма PV =3000 руб., наращенная сумма FV = 4500 руб., r = 20 % годовых (простые проценты). Тогда период начисления

Задача 2. Первоначальная сумма PV =5000 руб., наращенная сумма FV = 7200 руб., r = 10 % годовых (простые проценты). Найти период начисления.

Зная первоначальную сумму PV, наращенную сумму FV, период начисления n (в годах), можно определить простую годовую процентную ставку r:

12

Пример 4. Первоначальная сумма PV =2000 руб., наращенная сумма FV = 2200 руб., период начисления n = 0,5 года. Тогда простая процентная ставка

Задача 3. Найти простую процентную ставку, если известна первоначальная сумма 3000 руб., наращенная сумма 3300 руб. и период начисления 0,5 года.

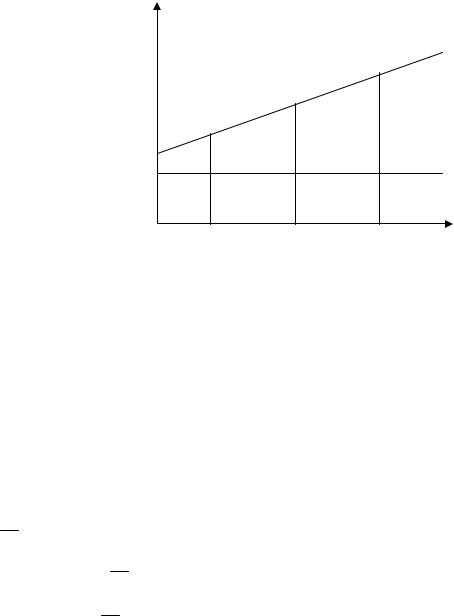
При наращении простых процентов процентные деньги растут в арифметической прогрессии. Графически это показано на рис. 2, где Р – начальная сумма, отрезки РкТк – наращенные суммы и отрезки РкМк – процентные деньги.

Р

Р

Р

Р

М1 М2 Мк

Рис. 2. Наращение простых про-

2.2.Английская, немецкая и французская практика начисления

Следует заметить, что задачи на формулу простых процентов на практике встречаются редко, поскольку к этим задачам прибегают в случаях:

−выдачи краткосрочных ссуд, т.е. ссуд, срок которых либо равен году, либо меньше его, с однократным начисление процентов;

−когда проценты не присоединяются к сумме долга, а периодически выплачиваются. В тех случаях, когда срок ссуды менее года, происходит модификация формулы

FV = PV*(1+r*n):

1)если срок ссуды выражен в месяцах (м), то величина n выражается в виде дроби:

n = 12M , тогда все формулы можно представить в виде:

FV = PV (1 + 12M * r) I = PV * r * 12M .

Пример 5. Изменим условия примера 2, снизив срок долга до 6 месяцев. Решение. Наращенная сумма:

13

FV = PV (1 + 12M * r) = 2000(1 +126 * 0,1) = 2100 руб.

Сумма начисленных процентных денег:

I = PV * r * 12M = 2000 * 0,1* 126 =100 руб. или I=FV-PV=2100-2000=100 руб.

таким образом, через полгода необходимо вернуть общую сумму в размере 2100 руб., из которой 2000 руб. составляет долг, а проценты – 100 руб.

2)если время выражено в днях (t), то величина n выражается в виде следующей дроби:

n = Tt ,

где t – число дней ссуды, т.е. продолжительность срока на который выдана ссуда; T – расчетное число дней в году (временная база).

Отсюда модифицированные формулы имеют вид:

FV = PV (1 + Tt * r)

I = PV * r * Tt

В мировой практике существует несколько способов определения срока возврата ссуд. Таким образом, расчет простых процентов может быть произведен одним из трех возмож-

ных способов:

а) обыкновенные проценты с приближенным числом дней ссуды, это способ называется немецким и часто упоминается как способ 360/360. число Т – продолжительность года условно принимают за 360 дней, целого месяца – за 30 дней, поэтому число t состоит из полного числа месяцев плюс точное число дней в оставшемся неполном месяце минус один день (день выдачи и день погашения ссуды считаются одним днем). Этот способ обычно используется в Германии, Дании, Швеции.

б) обыкновенные проценты с точным числом дней ссуды, или «французская практика расчета», когда продолжительность года условно принимается за 360 дней, а продолжительность ссуды рассчитывается точно по календарю минус один день (день выдачи и день погашения считаются одним днем). Этот способ имеет распространение во Франции, Бельгии, Испании, Швеции и обозначается АСТ/360.

в) точные проценты с точным числом дней ссуды, или «английская практика» (которая обозначается АСТ/АСТ), когда продолжительность года и продолжительность ссуды берутся точно по календарю (минус 1 день).

Для упрощения процедуры расчета точного числа дней финансовой операции пользуются специальными таблицами порядковых номеров дней года (см. Приложение), в которых все дни в году последовательно пронумерованы. Точное количество дней получается путем вычитания номера первого дня финансовой операции из номера последнего дня финансовой операции.

Пример 6. Сумма 3000 руб. положена в банк в 18 марта 2007 года по 20 октября 2007 года под r = 12 % годовых (простые проценты). Найти наращенную сумму при различной практике их начисления.

Решение. В немецкой практике начисления процентов продолжительность года Т = 360 дней, t = 14 (март) + 6*30 (апрель, май, июнь, июль, август, сентябрь) + 20 (октябрь) – 1 (день от-

14

крытия и день закрытия счета всегда считается за один день) = 213 дней. Тогда FV = PV (1 + Tt * r)

= 3000 * (1 + 360213 * 0,12) = 3213 руб.

Во французской практике: Т = 360 дней, t = 14 (март) + 30 (апрель) + 31 (май) + 30 (июнь) + 31 (июль) + 31 (август) + 31 (сентябрь) +20 (октябрь) – 1 (день открытия и день закрытия счета считаются всегда за один день) = 216 дней.

Тогда FV = PV (1 + Tt * r) = 3000 * (1 + 360216 * 0,12) = 3213,04 руб.

В английской практике: Т = 365 дней, t =216 дней.

Тогда FV = 3000 * (1 + 365216 * 0,12) ≈ 3213,04 руб.

Задача 4. Первоначальная сумма 2000 руб. помещена в банк под r = 15 % годовых (простые проценты) на срок с 19 февраля 2007 г. По 27 ноября 2007 г. Найти наращенную сумму в каждой из практик начисления процентов.

Как видно, результат финансовой операции во многом зависит от выбора способа начисления простых процентов. Поскольку точное число дней в большинстве случаев больше приближенного числа дней, то и проценты с точным числом дней ссуды обычно получаются выше процентов

сприближенным числом дней ссуды.

Впрактическом смысле эффект от выбора того или иного способа зависит от значительности суммы, фигурирующих в финансовых операциях.

2.3.Переменные ставки

Ставка процентов не является застывшей на вечные времена величиной, поэтому в финансовых операциях предусматривают дискретно изменяющиеся во времени процентные ставки. Пусть на интервалах начисления (в годах) n1, n2, …, nk применяются простые процентные ставки r1, r2, …, rk соответственно. Тогда наращенную сумму определяют по формуле:

FV= PV*(1+n1*r1+ n2*r2+…+ nk*rk) = PV * (1 +∑k n j * rj ) .

j=1

Пример 7. Вклад в сумме 3000 руб.был положен в банк. В первой половине года применялась простая процентная ставка r1 = 15 % годовых, во второй половине года – r2 = 12 % годовых. Определить наращенную сумму.

Решение. Наращенная сумма FV равна

FV= PV*(1+n1*r1+ n2*r2) = (1+0,5*0,15+0,5*0,12) = 3405 руб.

Задача 5. Вклад в сумме 5000 руб. был положен в банк 25 мая не високосного года по ставке 35 % годовых, а с 1 июля банк снизил ставку по вкладам до 30 % годовых и 15 июля вклад был востребован. Определить сумму начисленных процентов при английской практике начисления.

2.4.Сложные проценты

15

В финансовой практике значительная часть расчетов ведется с использованием схемы сложных процентов. Применение схемы сложных процентов целесообразно в тех случаях, когда:

−проценты не выплачиваются по мере их начисления, а присоединяются к первоначальной сумме долга. Присоединение начисленных процентов к сумме долга, которая служит базой для их начисления, называется капитализацией процентов;

−срок ссуды более года.

При наращении сложных процентов по ставке r каждая следующая сумма возрастает на долю r от предыдущей.

Таким образом, к концу единичного промежутка начисления суммы PV возрастет на долю r и станет FV1=PV+PV*r, к концу 2-го промежутка начисления эта сумма возрастет на долю r от FV1 и станет

FV2 = FV1+ r* FV1=PV*(1+r)+r*PV*(1+r)=PV*(1+r)*(1+r)=PV*(1+r)2 и т.д.

Тогда за n периодов начисления формула примет вид:

FV=PV*(1+r) n

При этом величину (1+r) n называют коэффициентом (множителем) наращения сложных процентов, который показывает во сколько раз возрастет за n лет сумма, положенная в банк под r процентов годовых.

Для облегчения расчетов коэффициенты наращения, зависящие от процентной ставки r и числа периода наращения n представлены в Приложении.

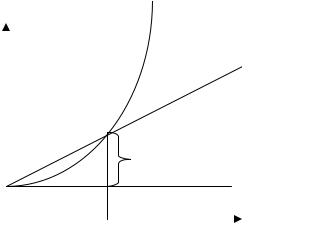
Сравнение силы роста простых и сложных процентов представлены на рис. 3.

(1+r)n

FV

1+n*r

r

1

n

1

Рис. 3. Сравнение силы роста простых и сложных процентов

Как видно из рис.2, при кратковременных ссудах начисление по простым процентам предпочтительнее, чем по сложным процентам, при сроке в один год разница отсутствует, но при среднесрочных и долгосрочных ссудах наращенная сумма значительно выше рассчитанная по сложным процентам, чем по простым.

Таким образом, для лиц, предоставляющих кредит:

−более выгодна схема простых процентов, если срок ссуды менее года (проценты начисляются однократно в конце года);

−более выгодной является схема сложных процентов, если срок ссуды превышает год;

−обе схемы дают одинаковый результат при продолжительности периода один год и однократном начислении процентов.

16

Достаточно часто в финансовых контрактах при предоставлении кредитов на срок, меньший 1 года, расчеты, как правило, по схеме простых процентов. При предоставлении кредитов на срок, больший 1 года, возможны три случая:

−расчет по схеме простых процентов;

−расчет по схеме сложных процентов;

−расчет по смешенной схеме.

В случае нецелого числа лет, расчет по смешанной схеме производится следующим обра-

зом:

1)с помощью наращения сложных процентов на сумму PV вычисляются процентные деньги за пользование кредитов в течении целого числа лет;

2)с помощью наращения простых процентов на накопленную к этому моменту сумму долга вычисляются процентные деньги за оставшуюся неполную часть года.

Пример 8. Пусть PV =3000000 ден. ед. ; r =0,16 %; n =3,4 года.

Решение. Для расчета по смешанной схеме «нарастим» сначала на сумму PV сложные проценты за 3 года:

FVх=PV*(1+r) n=3000000*1,163=46826889.

«Нарастим» теперь на FVх простые проценты за оставшиеся 0,4 года:

FV= FVх*(1+ r*n)=4682689(1+0,16*0,4)=4982380,03.

Итак при расчете по смешанной схеме заемщик через 3,4 года возвращает кредитору

4982380,03 (ден. ед.).

2.5.Внутригодовые процентные начисления

Вбанковской практике капитализация процентов может производиться несколько раз в год

–ежемесячно, ежеквартально, по полугодиям и т.д. Однако в условиях финансовых операций ука-

зывается не ставка за период, а годовая ставка с указанием периода начисления – номинальная ставка rm.

Номинальная ставка (nominal rate) – годовая ставка процентов, исходя из которой определяется величина ставки процентов в каждом периоде начисления, при начислении сложных процентов несколько раз в год.

Эта ставка

•во-первых, не отражает реальной эффективности сделки;

•во-вторых, не может быть использована для сопоставлений.

Если начисление процентов будет производиться m раз в год, а срок долга – n лет, то общее количество периодов начисления за весь срок финансовой операции составит

N = n *m

Отсюда формулу сложных процентов можно записать в следующем виде:

FV = PV*(1 + rm / m)N = P*(1 + r/m)m*n ,

где rm – номинальная годовая ставка процентов.

Пример 9. Сумма в размере 2000 руб. дана в долг на 2 года по ставке процента равной 10 % годовых. Найти проценты и сумму, если начисление ежеквартальное.

Решение: Количество периодов начисления:

N = m*n = 4 * 2 = 8

Наращенная сумма составит:

17

FV = PV * (1 + r / m)m*n = 2000 * (1 + 0,1 / 4 )8 = 2436,81 руб.

Сумма начисленных процентов:

I = FV - PV = 2436,81 - 2000 = 436,81 руб.

Таким образом, через два года на счете будет находиться сумма в размере 2436,81 руб., из которой 2000 руб. является первоначальной суммой, размещенной на счете, а 436,81 руб. – сумма начисленных процентов.

Наряду с номинальной ставкой существует эффективная ставка (effective rate), измеряющая тот реальный относительный доход, который получен в целом за год, с учетом внутригодовой капитализации. Эффективная ставка показывает, какая годовая ставка сложных процентов дает

тот же финансовый результат, что и m-разовое наращение в год по ставке rm / m: (1 + ref)n = (1 + rm / m)m * n,

следовательно,

ref = (1 + rm / m)m - 1.

Из формулы следует, что эффективная ставка зависит от количества внутригодовых начис-

лений.

Расчет эффективной ставки является мощным инструментом финансового анализа, поскольку ее значение позволяет сравнивать между собой финансовые операции, имеющие различные условия: чем выше эффективная ставка финансовой операции, тем (при прочих равных условиях) она выгоднее для кредитора.

Пример 10. Рассчитаем эффективную ставку для финансовой операции, рассмотренной в предыдущем примере, а также для вклада при ежемесячном начислении процентов по годовой ставке 10%.

Решение:

Эффективная ставка ежеквартального начисления процентов, исходя из 10% годовых, со-

ставит:

ref = (1 + rm / m)m - 1 = (1 + 0,1 / 4)4 - 1 = 0,1038.

Эффективная ставка ежемесячного начисления процентов будет равна: ref = (1 + rm / m)m - 1 = (1 + 0,1 / 12)12 - 1 = 0,1047.

Таким образом, годовая ставка, эквивалентная номинальной ставке процентов в размере 10% годовых при ежемесячном начислении процентов, составит 10,47% против 10,38% с ежеквартальным начислением процентов. Чем больше периодов начисления, тем быстрее идет процесс наращения.

Для облегчения расчетов можно пользоваться таблицами коэффициентов наращения сложных процентов, но внимательно следить за соответствием длины периода начисления и процентной ставки за этот же период. Например, если периодом начисления является квартал, то в расчетах должна использоваться квартальная ставка.

2.6.Вопросы и задачи для проверки усвоения пройденного материала

1.Дать определения процесса наращения.

2.Суть формулы простых процентов.

3.Какие существуют практики начисления процентов в мировой практике?

4.Расчет наращенной суммы в случае дискретно изменяющейся во времени процентной ставки по схеме простых процентов как вычисляется? (вывести аналогичную формулу по схеме сложных процентов)

5.Дать определения номинальной и эффективной ставок.

6.Как определить срок и процентную ставку финансовой операции?

18

7.Задачи для самостоятельного решения.

Задача 1. Пусть P=1 000 000, p= 0.12 , t=1,5. В каком случае плата за кредит больше: при расчете по схеме простых или сложных процентов?

Задача 2. Пусть P=3 000 000, p = 0.16, t =3,4. Найти сумму, возвращаемую кредитору в случае расчета по смешанной схеме.

Задача 3. Заемщик получил ссуду 1 000 000 руб., которую должен погасить одним платежом через 5 лет. Расчет производиться по схеме сложных процентов, причем первые 2 года годовая процентная ставка равна12 %, а в оставшееся время – 16%. Найти сумму, возвращаемую кредитору, и процентные деньги.

Задача 4. Сначала цена товара увеличилась на 60 %, а затем новая цена уменьшилась на 20 %.Что произошло с первоначальной ценой товара?

Задача 5. Банковский вклад, не тронутый в течение года, в конце этого года увеличивается на 5 %. На сколько процентов увеличится вклад, не тронутый в течение 4 лет?

Задача 6. Найти месячный темп инфляции, если за 2 месяца цена товара увеличилась с 6250 до

6760 .

Задача 7. В течение первых 3 месяцев темп инфляции был равен 3 % , а в течение следующих 2 месяцев – 4%. На сколько процентов увеличились цены за 5 месяцев?

Задача 8. Депозит рассчитывается по схеме простых процентов с годовой процентной ставкой 20 % .За какое время первоначальная сумма увеличиться в 3 раза?

Задача 9. Сумма 2 000 000 руб. взята в долг на срок 4,8 года с годовой процентной ставкой 10 % при условии погашения долга одним платежом в конце срока. Какую сумму нужно будет возвратить кредитору, если расчет ведется:

А) по схеме простых процентов? Б) по схеме сложных процентов? В) по смешанной схеме?

Задача 10. Сумма 2 000 000 руб. взята в долг на срок 3 года 9 месяцев с годовой процентной ставкой 10 % при условии погашения долга одним платежом в конце срока. Какую сумму нужно будет возвратить кредитору, если расчет производиться по схеме простых процентов с поквартальным реинвестированием процентов?

Задача 11. Заемщик получил ссуду 3 000 000 руб., которую должен погасить одним платежом через 1.5 года. Расчет производиться по схеме простых процентов, причем первые 0,75 года годовая процентная ставка равна 13 %, а в оставшееся время годовая процентная ставка равна 17%. Найти сумму , возвращаемую кредитору.

Задача 12. Заемщик получил 09.03.05 ссуду 600 000 долл., возвратить которую необходимо 29.07.05 , а расчет производится по схеме простых процентов с 13 %-ной годовой процентной ставкой

.Какую сумму должен возвратить заемщик кредитору при расчете: Задача 13. по английскому способу?

Задача 14. по французскому способу? Задача 15. по немецкому способу?

Задача 16. Годовая ставка простых процентов равна 8,3 %. Через сколько лет начальная сумма удвоится?

Задача 17. Пусть P=1000, r = 10 %. Найти наращенную сумму за n=3 промежутка начисления. Задача 18. Годовая ставка сложных процентов равна r = 8 %. Через сколько лет начальная сум-

ма удвоится?

Задача 19. Предприниматель получил в банке ссуду в размере 25 тыс. руб. сроком на 6 лет на следующих условиях: для первого года процентная ставка равна 10 % годовых, на следующие 2 года устанавливается маржа в размере 0,4 % и на последующие годы маржа равна 0,7 %. Найти сумму, которую предприниматель должен вернуть в банк по окончании срока ссуды по схеме простых и сложных процентов.

Задача 20. Товар ценой в 3 тыс. руб. продается в кредит на 2 года под 12 % годовых с ежеквартальными равными погасительными платежами, причем начисляются простые проценты. Определить долг с процентами, проценты и величину разового погасительного платежа.

Глава 3. ОПЕРАЦИИ ДИСКОНТИРОВАНИЯ

19

Математическое дисконтирование – определение первоначальной суммы долга, которая при начислении процентов по заданной величине процентной ставки ( i ) позволит к концу срока получить указанную наращенную сумму:

для простых процентов

PV = FV/(1 + n*r) = FV*1/(1 + n*r) = FV*(1 + n* r) -1 ,

где(1 + n*r) -1 – дисконтный множитель (коэффициент приведения) для простых процентов. Дисконтный множитель показывает, какую долю составляет первоначальная сумма долга в величине наращенной суммы. Поскольку дисконтный множитель (множитель приведения) зависит от двух аргументов (процентной ставки и срока ссуды), то его значения легко табулируются, что

облегчает финансовые расчеты.

Пример 1. Через 150 дней с момента подписания контракта необходимо уплатить 310 тыс. руб., исходя из 8% годовых и временной базы 360 дней. Определить первоначальную сумму долга.

Решение:

Поскольку срок ссуды менее года, то используем формулу простых процентов:

PV = FV* 1/ (1 + t/ T * r) =

= 310000* 1 / (1 + 150 / 360* 0,08) = 300000 руб.

Таким образом, первоначальная сумма долга составила 300 тыс. руб., а проценты за 150 дней – 10 тыс. руб.

Для сложных процентов

PV = FV* (1 + r) -n ,

где (1 + r) -n – дисконтный множитель для сложных процентов, который также табулируется (см. Приложение)

Если начисление процентов производится m раз в год, то формула примет вид:

PV = FV *(1 + r / m) -m*n .

Пример 2. Через два года фирме потребуется деньги в размере 30 млн руб., какую сумму необходимо сегодня поместить в банк, начисляющий 25% годовых, чтобы через 2 года получить требуемую сумму?

Решение:

Поскольку срок финансовой операции составляет более года, что используем формулу при-

ведения для сложных процентов:

PV = FV* 1 / (1 + r) n =

= 30000000* 1 / (1 + 0,25)2 = 19200000 руб.

Таким образом, фирме следует разместить на счете 19200000 руб. под 25% годовых, чтобы через два года получить желаемые 30000000 руб.

Современная величина и процентная ставка, по которой проводится дисконтирование, находятся в обратной зависимости: чем выше процентная ставка, тем при прочих равных условиях меньше современная величина.

В той же обратной зависимости находятся современная величина и срок финансовой операции: чем выше срок финансовой операции, тем меньше при прочих равных условиях современная величина.

3.3.Банковский учет

Банковский учет – второй вид дисконтирования, при котором исходя из известной суммы в будущем, определяют сумму в данный момент времени, удерживая дисконт.

Операция учета (учет векселей) заключается в том, что банк или другое финансовое учреждение до наступления платежа по векселю покупает его у предъявителя по цене ниже суммы век-

21

селя, т.е. приобретает его с дисконтом. Сумма, которую получает векселедержатель при досрочном учете векселя, называется дисконтированной величиной векселя. При этом банк удерживает в свою пользу проценты (дисконт) от суммы векселя за время, оставшееся до срока его погашения. Подобным образом (с дисконтом) государство продает большинство своих ценных бумаг.

Определение 1. Векселем называется безусловное письменное обязательство векселедателя (заемщика) выплатить векселедержателю (кредитору) в указанное время и в указанном месте ука-

занную сумму (номинальную стоимость векселя).

Определение 2. Учетом (дисконтированием) векселя называется его покупка по цене, меньшей номинальной стоимости.

Определение 3. Дисконтом называется разница между номинальной стоимостью векселя и ценой его покупки.

Для расчета дисконта используется учетная ставка:

•простая учетная ставка:

D = FV - PV = FV * n* d = FV *t / T *d ,

где n – продолжительность срока в годах от момента учета до даты выплаты известной суммы в будущем.

Отсюда:

PV = FV - FV * n * d = FV *(1 - n *d),

где (1 - n * d) – дисконтный множитель.

Очевидно, что чем выше значение учетной ставки, тем больше дисконт. Дисконтирование по простой учетной ставке чаще всего производится по французской практике начисления процентов, т.е. когда временная база принимается за 360 дней, а число дней в периоде берется точным.

Пример 3. Вексель выдан на 5000 руб. с уплатой 17 ноября, а владелец учел его в банке 19 августа по учетной ставке 8%. Определить сумму, полученную предъявителем векселя и доход банка при реализации дисконта.

Решение:

Для определения суммы при учете векселя рассчитываем число дней, оставшихся до погашения обязательств:

t = 13 (август) + 30 (сентябрь) + 31 (октябрь) + 17 (ноябрь) - 1 = 90 дней.

Отсюда, определяемая сумма:

PV = FV *(1 - t / T *d) = 5000 *(1 - 90 / 360* 0,08) = 4900 руб.

Тогда дисконт составит:

D = FV - PV = 5'000 - 4900 = 100 руб.

или

D = FV* t / T *d = 5000 *90 / 360* 0,08 = 100 руб.

Следовательно, предъявитель векселя получит сумму 4900 руб., а банк при наступлении срока векселя реализует дисконт в размере 100 руб.

• по сложной учетной ставке:

PV = FV *(1 - d) n

При использовании сложной учетной ставки процесс дисконтирования происходит с прогрессирующим замедлением, т.к. учетная ставка каждый раз применяется к уменьшаемой на величину дисконта величине.

Пример 4. Определить величину суммы, выдаваемую заемщику, если он обязуется вернуть ее через два года в размере 55 тыс. руб. Банк определяет свой доход с использованием годовой учетной ставки 30%.

Решение:

Используя формулу дисконтирования по сложной учетной ставке, определяем:

22

PV = FV* (1 - d) n = 55000* (1 - 0,3)2 = 26950 руб.

Заемщик может получить ссуду в размере 26950 руб., а через два года вернет 55 тыс. руб.

В том случае, когда учету подлежит долговое обязательство, по которому предусматривается начисление процентов, происходит совмещение начисления процентов по процентной ставке и дисконтирования по учетной ставке:

PV2 = PV1* (1 + n1* r)* (1 - n2* d ),

где PV1 – первоначальная сумма долга;

PV2 – сумма, получаемая при учете обязательства; n1 – общий срок платежного обязательства;

n2 – срок от момента учета до погашения.

Пример 5. Обязательство уплатить через 100 дней сумму долга в размере 50 тыс. руб. с начисляемыми на нее точными процентами по ставке 40%, было учтено за 25 дней до срока погашения по учетной ставке 25%. Определить сумму, полученную при учете обязательства.

Решение:

Следует обратить внимание на различие временных баз, используемых при наращении и

учете:

PV2 = PV1* (1 + n1 * r) • (1 - n2* d ) =

= 50'000* (1 + 100 / 365* 0,4)* (1 - 25 / 360* 0,25) = 54516 руб.

Следовательно, сумма, получаемая при учете данного обязательства, составит 54516 руб.

3.4.Ломбардный кредит

Для получения ломбардного кредита заемщик должен передать кредитору в качестве залога материальные ценности или ценные бумаги. Получив залог, кредитор производит оценку его текущей рыночной стоимости и предоставляет заемщику ссуду по схеме простых процентов на основе учетной ставки, причем кредитное соглашение заключается так, чтобы возвращаемая заемщиком кредитору долговая сумма (с учетом процентных денег и расходов кредитора по обслуживанию долга) не превышала 50-85 % стоимости залога.

Ломбардный кредит обычно выдается на срок 3 месяца, а погашение осуществляется по одному из следующих вариантов:

1)заемщик может погасить весь долг вовремя;

2)заемщик может продлить срок погашения долга на следующие 3 месяца;

3)заемщик может погасить вовремя лишь часть долга, а оставшуюся часть погашать в течение следующих 3 месяцев.

При расчетах процентных денег учитывается точное число дней в каждом месяце, а год принимается равным 360 дням. День выдачи и день погашения ломбардного кредита считаются одним днем.

Если заемщик не погасит долг вовремя, то он, как правило, за время просрочки платежа рассчитывается с кредитором по увеличенной (штрафной) ставке.

В случае, если заемщик не может (или не хочет) полностью рассчитаться с кредитором, кредитор реализует залог в установленном законом порядке.

Пример 6. Клиент обратился в банк за получением ломбардного кредита и передал в залог 150 акций. Банк согласился предоставить кредит на 3 месяца исходя из 80 % курсовой стоимости

23

акций. Годовая учетная ставка равна 18 %, а затраты банка по обслуживанию долга в течение 3 месяцев – 200 руб. На какой кредит может рассчитывать клиент банка, если текущий курс его акций составляет 300 руб. за акцию, а кредит выдается с 16.03.04 по 16.06.04?

Решение. Совокупная стоимость ценных бумаг заемщика равна

300 руб. * 150 = 45000 руб.,

Следовательно, заемщик должен возвратить банку

FV = 45000*0,8=36000 руб.

Найдем время n пользования кредитом в годах. При пользовании кредитом 16.03.04 по 16.06.04 время n можно рассчитать по формуле:

n = Tt = 36091 = 0,2528 ,

где t =91 – срок кредита в днях; Т = 360 – количество дней в году.

D = FV*r*t=36000*0,18*0,2528=1638 руб.

Теперь найдем сумму, которую получит «на руки» заемщик. Для этого нужно из суммы FV вычесть процентные деньги и затраты банка по обслуживанию долга

PV= FV- D-200=36000-1638-200=34162

Ответ. Заемщик 16.03.04 получает 34162 руб. и должен возвратить 16.06.04 банку 36000

руб.

Пример 7. Продолжая предыдущую задачу, предположит, что заемщик выплатил 16.06.04 банку только часть долга – 6000 руб. и попросил продлить срок погашения долга еще на 3 месяца. Банк согласился продлить срок погашения, увеличив учетную ставку до 20 %. Сколько должен будет заплатить заемщик банку 16.09.04?

Решение. Сначала найдем остаток долга на 16.06.04:

PV1 = 36000-6000=30000.

Воспользовавшись формулой, определим возвращаемую заемщиком сумму FV1 за 91 день использования кредитом 30000 руб. в период с 16.06.04 по 16.09.04 (d = 0,2 – учетная ставка):

Таким образом, с учетом расходов банка по обслуживанию долга заемщик должен 16.09.04

заплатить банку 31597,43+200=31797,43 руб.

Ответ. Заемщик 16.09.04 должен заплатить банку 31797,43 руб.

3.5.Вопросы и задачи для проверки усвоения пройденного материала

1.Что такое дисконтирование?

2.В чем суть банковского учета?

3.В чем суть математического и банковского дисконтирования?

4.Какой вид дисконтирования выгоднее для векселедержателя?

5.Назовите формулу дисконтирования по сложным процентам и простой учетной

ставке.

6.Вексель на сумму 300000 руб. со сроком погашения 16.07.04 г. Учитывается банком

16.04.04по простой учетной ставке 9 %. Найти дисконтированную цену векселя, используя способ расчета 365/360.

24

7.Задачи для самостоятельного решения

Задача 1. Ломбард предоставляет кредиты под залог ювелирных изделий исходя из 50 % текущей рыночной стоимости изделия на основе годовой учетной ставки 30 % на срок 3 месяца. Клиент передал в ломбард золотой браслет. Эксперт ломбарда оценил рыночную стоимость браслета в 10 000 руб. Какую сумму получит клиент и какую сумму он должен возвратить ломбарду?

Задача 2. Депозит в 200 тыс. руб. положен в банк на 4 года под 15 % годовых. Найти наращенную сумму, если ежегодно начисляются сложные проценты.

Задача 3. Клиент обратился в банк 12 апреля с целью получения кредита под залог 300 ценных бумаг, причем курсовая стоимость каждой ценной бумаги на этот день составляет 100 рублей. Банк предоставляет кредит под 10 % годовых на 3 месяца в размере 80% курсовой стоимости ценных бумаг. В контракте с клиентом оговаривается, что затраты банка на обслуживание долга составляют 1 % от номинальной суммы кредита и удерживаются вместе с процентным платежом в момент предоставления кредита. В случае просрочки выплаты долга клиент рассчитывается с банком за каждый лишний день по ставке 12 % годовых. Найти величину кредита, который получит клиент.

Задача 4. Предпринимателю необходима сумма в 40 тыс. руб. на 3 месяца. Банк предоставит ему кредит в размере 75 % от стоимости залога под 12 % годовых и за обслуживание долга взыщет 400 руб. Определить величину залога, если кредит взят 15 мая.

Задача 5. По договоренности с кредитором для оплаты векселя номинальной стоимостью F = 1 000 000 руб. и сроком платежа 18.04.03 заемщик выписывает 18.04.03 кредитору четыре векселя на основе простой годовой учетной ставки 6% в соответствии с табл.1 .Найти номинальную стоимость векселей 3 и 4 , используя способ расчета 365/360.

Таблица 1

Задача 6. Банк А имеет обязательства оплатить 18.06.03 банку Б векселя на сумму F=860 000 долл. . В качестве частичной оплаты банк А сдает в переучет (редисконт) банку Б три векселя на основе простой годовой учетной ставки 9 % в соответствии с таблицей 2. Найти остаток долга , используя способ расчета 365/360, если затраты банка Б на операцию переучета составляют 100 долл.

25

Глава 4. ПОТОКИ ПЛАТЕЖЕЙ И ФИНАНСОЫЕ РЕНТЫ

Очень часто в контрактах финансового характера предусматривают не отдельные разовые платежи, а серию платежей, распределенных во времени. Предположим, что ссуда размером PV с годовой процентной ставкой r, предоставленная на срок n (в годах) и предусматривающая погашение долговой суммы (с учетом процентных денег) при помощи m одинаковых платежей, осуществляемых через равные периоды времени, причем в случае простых процентов размер каждого погашающего платежа равен

A = PVm

а в случае сложных процентов размер каждого погашающего платежа равен

A = PVm

Определение: Платежи, осуществляемые в начале периодов времени, называются платежами пренумерандо, а в конце периодов – платежами постнумерандо.

4.1.Потребительский кредит

Ранее мы рассматривали случаи, когда долг вместе с процентными деньгами возвращался заемщиком кредитору одним платежом в конце срока, установленного кредитным соглашением.

Далее рассматриваются случаи, когда ссуда выделяется заемщику целиком, а возвращается (погашается) несколькими платежами, которые могут быть одинаковыми или изменяться, например, в арифметической или геометрической прогрессии.

В одних случаях заемщику выгодно погашать ссуду одинаковыми платежами, так как это позволяет равномерно распределить тяжесть задолженности на весь срок ссуды. В других случаях заемщику может быть невыгодно погашать ссуду одинаковыми платежами, если в первое время после начала инвестирования финансовые поступления слишком малы для возврата долга.

Определение. Потребительским кредитом называется ссуда размером PV с годовой процентной ставкой r, предоставленная на срок n (в годах) и предусматривающая погашение долговой суммы (с учетом процентных денег) при помощи m одинаковых платежей, осуществляемых через равные периоды времени, причем в случае простых процентов размер каждого погашающего платежа равен

а в случае сложных процентов размер каждого погашающего платежа равен

Пример 1. Покупатель обратился в банк с просьбой о предоставлении кредита на покупку телевизора стоимостью 9000 руб. Банк предоставил покупателю потребительский кредит на срок 1,5 года с расчетом по схеме простых процентов на основе годовой процентной ставки 12 % с ежемесячными погашениями постнумерандо. Какую сумму денег покупатель должен ежемесячно перечислять банку?

26

Решение. Поскольку m = 18; r = 0,12; n = 1,5; PV = 9000, то, воспользовавшись формулой (1), получим

A = 181 (1 +1,5 * 0,12) = 590.

Ответ. Покупатель должен ежемесячно перечислять банку 590 руб.

Пример 2. Покупатель обратился в банк с просьбой о предоставлении кредита на покупку автомобиля стоимостью $ 18000. Банк предоставил покупателю потребительский кредит на срок 3 года с расчетом по схеме сложных процентов на основе годовой процентной ставки 9 % с ежемесячными погашениями постнумерандо. Какую сумму денег покупатель должен ежемесячно перечислять банку?

Решение. Поскольку m = 36; r = 0,09; n = 3; PV = 18000, то, воспользовавшись формулой (2), получим

A = 361 *18000 * (1 +0,09)3 =647,51.

Ответ. Покупатель должен ежемесячно перечислять банку $ 647,51.

Потребительский кредит очень привлекателен для кредитора и крайне несправедлив по отношению к заемщику. Конечно, в случае потребительского кредита кредитор получает от заемщика те же самые процентные деньги, как и в случае ссуды, возвращаемой одним платежом в конце срока. Но в отличие от такой ссуды в случае потребительского кредита кредитор начинает получать от заемщика погашающие платежи заранее и у него появляется возможность совершенно бесплатно пустить их в дело, предоставив, например, потребительский кредит другому клиенту. В результате кредитор получает такую плату за кредит, которая значительно превышает сумму процентных денег, выплаченных заемщиком.

Докажем это на ряде примеров. Рассмотрим сначала случай потребительского кредита с расчетом по схеме простых процентов.

Пример 3. Произведем расчет платы за кредит, описанный в примере 1, с точки зрения кредитора.

Решение. До момента внесения заемщиком последнего платежа (конец 18-го месяца) кредитор пользуется в течение 17 месяцев платежом 590 руб., выплаченным заемщиком в конце 1-го месяца. Сумма 590 руб., полученная кредитором в конце 1-го месяца, эквивалентна по простой процентной ставке 12 % сумме

590 * (1 +0,121712) = 690,3 (руб.),

полученной в конце 18-го месяца. Также до момента внесения заемщиком последнего платежа кредитор пользуется в течении 16 месяцев платежом в размере 590 руб., выплаченным заемщиком в конце 2-го месяца, эквивалентна по простой процентной ставке 12 %

590 * (1 +0,121612) = 684,4 (руб.),

полученной в конце 18-го месяца. Рассуждая аналогично, получаем, что третий платеж эквивалентен сумме

27

и т.д. Возникает убывающая арифметическая прогрессия {an },содержащая 18 членов

а1 = 690,3; а2 =684,4; а3 =678,5; …; а18 =590,

разность d которой равна

d = 590(1 +0,12 1612) −590(1 +0,121712) = −590(0,12 121 ) = −5,9 .

Найдем сумму этой арифметической прогрессии:

a1 + a2 +... + a18 = a1 +2a18 18 = 690,32+59018 =11522,7 .

Отсюда следует, что «в действительности» плата за кредит равняется

11522,7 – 9000 = 2522,7 руб.

Для сравнения подсчитаем процентные деньги в условиях примера 1:

D = PV*n*r = 9000 * 0,12 128 =1620 .

Таким образом, «в действительности» кредитор получает на 2522,7-1620=902,7 (руб.) больше, чем указано в кредитном соглашении.

Ответ. «В действительности» кредитор получает на 902,7 руб. больше, чем указано в кредитном соглашении.

Перейдем к случаю потребительского кредита с расчетом по схеме сложных процентов.

Пример 4. Произведем расчет платы за кредит, описанный в примере 2, с точки зрения кредитора.

Решение. До момента внесения заемщиком последнего платежа (конец 36-го месяца) кредитор пользуется в течение 35 месяцев платежом в размере $ 647,51, выплаченным заемщиком в конце 1-го месяца. Сумма $ 647,51, полученная кредитором в конце 1-го месяца, эквивалентна по сложной процентной ставке 9 % сумме

35

647,51(1+0,09)12 = 832,54 ,

полученной в конце 36-го месяца. Также до момента внесения заемщиком последнего платежа кредитор пользуется в течение 34 месяцев платежом в размере $ 647,51, выплаченным заемщиком в конце 2-го месяца. Сумма $ 647,51, полученная кредитором в конце 2-го месяца, эквивалентна по сложной процентной ставке 9 % сумме

34

647,51(1 +0,09)12 = 826,55 ,

полученной в конце 36-го месяца. Рассуждая аналогично, находим, что третий платеж эквивалентен сумме

33

647,51(1+0,09)12 = 820,6

и т.д. Возникает убывающая геометрическая прогрессия {bn }, содержащая 36 членов

b1 = 832,54; b2 = 826,55; b3 = 820,6; …; b36 = 647,51,

знаменатель которой

28

− 1

q =1,09 12 = 0,9928 .

Найдем сумму этой геометрической прогрессии:

Отсюда следует, что «в действительности» плата за кредит равняется 26345,83 – 18000 = 8345,83 (долл.). Для сравнения подсчитаем процентные деньги в усло-

виях примера 2:

D = PV (1 + r)n − PV =18000((1 +0,09)3 −1) = 5310,36 .

Таким образом, «в действительности» кредитор получает на 8345,83-5310,36=3035,47 долл. больше, чем указано в кредитном соглашении.

За счет чего же кредитор получает дополнительную плату за кредит, описанную в примерах

3 и 4? За счет того, что он длительное время бесплатно пользуется деньгами заемщика, посту-

пившими к нему в качестве погашающих платежей.

4.2. Погашение ссуд одинаковыми платежами, на которые начисляются процентные деньги

Данный параграф посвящен методу погашения ссуд посредством одинаковых платежей, осуществляемых через равные периоды времени. Однако в отличие от 4.1 в счет погашения ссуды идут не только погашающие платежи, но и начисленные на них процентные деньги, что гораздо более справедливо по отношению к заемщику.

Определение. Платежи , осуществляемые ежегодно , называются аннуитетами.

Пример 5. Заем $150 000, предоставленный на срок 4 года с расчетом по схеме простых процентов с годовой процентной ставкой 10 %, погашается одинаковыми аннуитетами постнумерандо. Кредитор по такой же схеме рассчитывает процентные деньги за пользование каждым аннуитетом с момента его получения и до срока окончания займа, которые идут в счет погашения займа. Найти значения аннуитетов.

Решение. По условию задачи PV =150000, r = 0,1; n=m=4. Получим сначала формулу, позволяющую найти значения А аннуитетов для произвольных значений P, r, m, а затем подставим в эту формулу числовые данные решаемой задачи.

Поскольку кредитор пользуется первым аннуитетом в течение (n-1) года, вторым аннуитетом – в течение (n-2) лет и т.д., то воспользовавшись для расчета процентных денег формулой простых процентов, составим следующее уравнение

A(1+(n-1)*r+ A(1+(n-2)*r+ … + A=PV(1+n*r). (3)

Из уравнения (1) легко находится аннуитет

С помощью формулы для суммы арифметической прогрессии

(1+(n-1)r)+(1+(n-2)r+…+1= 2 +(n −1)r n 2

29

Очевидно, что размер погашающего платежа $ 45652,17, рассчитаны по формуле (6), гораздо предпочтительнее для заемщика, чем погашающего платежа $ 52500, рассчитанного по (7).

Ответ. Аннуитет равен $ 45652,17.

Перейдем к случаю сложных процентов.

Пример 6. Заем $ 200 000, предоставленный на срок 5 лет с расчетом по схеме сложных процентов с годовой процентной ставкой 6 %, погашается одинаковыми аннуитетами постнумерандо. Кредитор по такой же схеме рассчитывает процентные деньги за пользование каждым аннуитетом с момента его получения и до срока окончания займа, которые идут в счет погашения займа. Найти аннуитеты.

Решение. По условию задачи PV =200000, r=0,06, n=m=5. Получим сначала формулу, позволяющую найти значение А аннуитетов для произвольных PV, r, n, а затем подставим в эту формулу числовые данные решаемой задачи.

Поскольку кредитор пользуется первым аннуитетом в течение (n-1) года, вторым аннуитетом – в течении (n-2) лет и т.д., то, воспользовавшись для расчета процентных денег формулой сложных процентов, составим следующее уравнение:

Для сравнения подсчитаем аннуитеты, когда на аннуитеты не начисляются процентные деньги:

30

Очевидно, что размер погашающего платежа $ 47479,28, рассчитанный по формуле (11), гораздо предпочтительнее для заемщика, чем размер погашающего платежа $ 53529,02, рассчитанный по формуле (12).

Ответ. Аннуитет равен $ 47479,28.

4.3. Погашение ссуд одинаковыми платежами в случае, когда процентные деньги погашаются в зависимости от остатка долга

Разделение погашающих платежей на две части, отвечающие за погашение долга и погашение процентных денег, принципиально важно, поскольку от этого зависят уплачиваемые налоги.

Данный параграф посвящен методу погашения ссуд, предоставленных по схеме простых или сложных процентов с годовой процентной ставкой r %, при котором часть каждого погашающего платежа, идущая на погашение процентных денег, равна r % от существующего в момент совершения погашающего платежа остатка долга (без учета процентных денег).

Рассмотрим применение этого метода на решении примера 7 и является продолжением примера 6.

Пример 7. Заем $ 200000, предоставленный на срок 5 лет с расчетом по схеме сложных процентов с годовой процентной ставкой 6 %, погашается аннуитетами $ 47479,28 постнумерандо. Часть каждого аннуитета, идущая на погашение процентных денег, составляет 6 % существующего в момент совершения погашающего платежа остатка долга (без учета процентных денег). Составить план погашения займа (результаты сравнить с табл.1).

Решение. Введем следующие обозначения:

D1, D2, D3, D4, D5 – процентные платежиза 1, 2, 3, 4, 5-й годы соответственно (части аннуитетов, идущие на погашение процентных денег);

В1, В2, В3, В4, В5 – выплаты долга за 1, 2, 3, 4, 5-годы соответственно (части аннуитетов, идущие на погашение долга);

Z1, Z2, Z3, Z4, Z5 – остатки долга после внесения 1, 2, 3, 4, 5-го аннуитетов соответственно; А = 47479,28 – размер каждого аннуитета.

Таким образом,

D = D1+D2+ D3+ D4+ D5,

Z = В1+В2+В3+В4+В5.

Найдем первый процентный платеж D1:

D1 = 200000*0,06 = 12000.

Первая выплата по погашению долга представляет собой разность между аннуитетом и процентным платежом:

В1 = А - D1 =47479,28 – 12000 = 35479,28.

Следовательно, после первого погашения долг сокращается на $ 35479,28 и оказывается равным

Z1 = Z – B1 = 200000-35479,28 = 164520,72.

Вычислим процентный платеж на остаток долга:

D2 = 164520,72*0,06 = 9871,24.

31

Вторая выплата долга

В2 =А - D2 = 47479,28-9871,24 = 37608,04.

Далее по аналогии находим:

Z2 = Z1 - В1 = 164520,72-37608,04 = 126912,68; D3 = 126912*0,06 = 7614,76;

В3 = 47479,28-7614,76 = 39864,51; Z3 = 126912,68-39864,51 = 87048,16; D4 = 87048,16*0,06 = 5222,88;

В4 = 47479,28-5222,88 = 42256,4; Z4 = 87048,16-42256,4 = 44791,76; D5 = 4479,76*0,06 = 2687,52;

В5 = 47479,28-2687,52 = 44791,76;

Если из остатка долга вычесть последнюю выплату, получим

Z5 = Z4 - В5 = 44791,76-44791,76 = 0.

Ответ. Представим план погашения займа в форме таблицы 1.

Таблица 1. План погашения займа

4.4. Погашение ссуд платежами, содержащими одинаковые выплаты долга, в случае, когда процентные деньги погашаются в зависимости от остатка долга

Пример 8. Заем $ 150 000, предоставленный на срок 5 лет с расчетом по схеме сложных процентов с годовой процентной ставкой 5 %, погашается аннуитетами постнумерандо с одинаковыми выплатами долга. Процентные деньги на аннуитеты не начисляются. Часть каждого аннуитета, идущая на погашение процентных денег , составляет 5 % от существующего в момент совершения погашающего платежа остатка долга (без учета процентных денег). Составить план погашения займа.

Решение. Обозначим символами А1, А2, А3, А4, А5 аннуитеты за 1, 2, 3, 4, 5-й годы соответственно (в рассматриваемой задаче они различны). Так как

PV = 150000, r = 0,05, n = 5,

То ежегодные выплаты долга

В1 =B2 = B3 = B4 = B5 = Z/5=150000/5 = 30000.

Первый процентный платеж

D1 = PV* r = 150000*0,05 = 7500,

следовательно, аннуитет

32

А1 = В1 + D1 = 30000+7500 = 37500.

Поскольку после первой выплаты долг уменьшается на сумму В1 , то и процентный платеж, значит, и аннуитет, уменьшаются на соответствующий процент от выплаты В1:

А2 = А1 – В1*r = 37500-30000*0.05 = 37500-1500 = 36000.

Аналогичным образом находим

А3 = А2 – В1*r = 36000-1500 = 34500, А4 = А3 – В1*r = 34500-1500 = 33000, А5 = А4 – В1*r = 33000-1500 = 31500.

Ответ. Представим план погашения займа в форме в таблице 2. Таблица 2. План погашения займа

4.5. Погашение ссуд выплатами, изменяющимися в арифметической прогрессии, в случае, когда процентные деньги погашаются в зависимости от остатка долга

Пример 9. Заем в размере $ 200 000 погашается в течение 5 лет аннуитетами постнумерандо, причем выплаты долга от года к году:

1)увеличиваются на $ 5000,

2)уменьшаются на $ 5000.

Годовая ставка простых процентов равна 6 %. Процентные деньги на аннуитеты не начисляются. Составить план погашения займа в каждом из этих случаев.

Решение. а) Так как PV = 200 000, r = 0,06, n = 5, d = 5000 (разность арифметической прогрессии), то первая выплата В1 долга находится из уравнения

2B1 + d (n −1) n = PV , 2

Левая часть которого есть сумма n первых членов арифметической прогрессии. Следовательно, первая выплата долга

В1 = PV/n-d(n-1)/2=200 000/5-5000(5-1)/2 = 30 000,

первый процентный платеж

D1 = 200 000*0,06 = 12 000,

а первый аннуитет

А1 = В1 + D1 = 42 000.

Поступая аналогично, составим таблицу 3.

Таблица 3. План погашения займа в случае а.

33

б) Этот случай отличается от случая а лишь тем, что d = -5000 и первая выплата долга

В1 = PV/n-d(n-1)/2=200 000/5+5000(5-1)/2 = 50 000.

План погашения займа в случае б задается табл. 4.

Таблица 4. План погашения займа в случае б.

Ответ. В случаях а и б планы погашения займа представлены в таб. 3 и 4 соответственно.

4.6. Погашение ссуд выплатами, изменяющимися в геометрической прогрессии, в случае, когда процентные деньги погашаются в зависимости от остатка долга

Пример 10. Заем в размере $ 200 000. Погашается в течение 5 лет аннуитетами постнумерандо, причем выплаты долга от года к году:

1)увеличиваются на 5 %;

2)уменьшаются на 5 %.

Процентная ставка сложных процентов равна 10 %. Процентные деньги на аннуитеты не начисляются. Составить план погашения займа в каждом из этих случаев.

Решение. а) По условию задачи PV = 200 000, r = 0,1, n = 5, а знаменатель геометрической прогрессии q = 1,05

B1 qn −−1 = PV , q 1

С помощью которой можно найти первую выплату В1:

В1 = PV (q-1)/(qn-1)= 200 000(1,05-1)/(1,055-1) = 36 195.

Первый процентный платеж

D1 = 200 000*0,1 = 20 000,

34

а первый аннуитет

А1 = В1 + D1 = 56 195.

Поступая аналогично, составим таблицу 5.

Таблица 5. План погашения займа в случае а.

б) Этот случай отличается от случая а лишь тем, что q = 1-0,05 = 0,95 и первая выплата

В1 = PV (1-q)/(1-qn) = 200 000(1-0,95)/(1-0,955) = 44 204,74.

Действуя, как в случае а, составим табл. 5.

Таблица 6. План погашения займа в случае б.

Ответ. В случаях а и б планы погашения займа представлены в таб. 5 и 6 соответственно.

4.7. Погашение ссуд аннуитетами, последний из которых может отличаться от остальных, в случае, когда процентные деньги погашаются в зависимости от остатка долга

Пример 11. Заем в размере $ 8 000 000 погашается аннуитетами, каждый из которых, за исключением последнего, составляет 35 % займа. Заем предоставляется на основе сложных процентов с годовой процентной ставкой 5 %. Процентные деньги на аннуитеты не начисляются. Составить план погашения займа и определить последний аннуитет.

Решение. Сначала найдем все аннуитеты, за исключением последнего:

А = 8 000 000*0,35 = 2 800 000.

Первый аннуитет состоит из первой выплаты долга и процентного платежа. Первый процентный платеж D1:

35

D1 = 800 000 000*0,05 = 400 000.

Первая выплата долга:

В1 = А - D1 =2 800 000 – 400 000 = 2 400 000.

Остаток долга после первой выплаты

Z1 = Z – B1 = 8 000 000-2 400 000 = 5 600 000.

Далее получаем

D2 = 5 600 000*0,05 = 280 000,

В2 =А - D2 = 2 800 000-280 000 = 2 520 000,

Z2 = Z1 – В2 = 5 600 000-2 520 = 3 080 000, D3 = 3 080 000*0,05 = 154 000,

В3 = А – D3 = 2 800 000-154 000 = 2 646 000,

Z3 = Z2 – В3 = 3 080 000-2 646 000 = 434 000.

Заметим, что остаток долга Z3 оказался меньше предыдущих аннуитетов, и найдем процентный платеж

D4 = 434 000*0,05 = 21 700.

На этом шаге размер выплаты долга совпадает с остатком долга

В4 = Z3 = 434 000,

а аннуитет оказывается равным

В4 + D4 = 434 000+21 700 = 455 700.

Ответ. План погашения займа представлен в таблице 7.

Таблица 7. План погашения займа

4.8.Постоянные финансовые ренты

Определение. Финансовой рентой называется последовательность платежей, осуществляемых через одинаковые промежутки времени.

Определение. Постоянной финансовой рентой называется финансовая рента с одинаковыми платежами, в противном случае она называется переменной.

Определение. Финансовая рента называется конечной, если количество платежей ограничено, в противном случае она называется бесконечной.

Финансовые ренты часто встречаются в повседневной жизни. Простейшим примером является заработная плата (всегда ли?), пенсионные платежи, погасительные платежи в потребитель-

36

ском кредите, арендные платежи, платежи в различные фонды и т.д. За пользование рентными суммами, как правило, начисляются процентные деньги.

Пример 12. В первый день каждого месяца, начиная с 1 января 2004 года, вкладчик помещает на свой счет в банке 1 000 руб. Расчет производиться по схеме простых процентов с годовой процентной ставкой 6% и помесячным начислением процентных денег, причем год считается состоящим из 12 месяцев по 30 дней. Какая сумма окажется на счете 31 декабря 2013 года?

Решение. На первую сумму, внесенную на счет, процентные деньги начисляются в течение 120 месяцев, а за каждый месяц наращивается 6 %/12 = 0,5 %

поэтому к 31 декабря 2013 г. первая сумма превращается в сумму

F1 = 1000(1+0,005*120) = 1600

На вторую сумму, внесенную на счет, процентные деньги начисляются в течение 119 месяцев, и к 31 декабря 2013 г. она превращается в сумму

F2= 1000(1+0,005*119) = 1595.

Третья внесенная на счет сумма превращается в сумму

F3 = 1000(1+0,005*118) = 1590

и т.д. Таким образом, возникает убывающая арифметическая прогрессия F1, F2, … , F20 с первым членом 1600 и разностью (-5), последний член которой

F120 = 1000(1+0,005) = 1005.

Сумма этой арифметической прогрессии

S = 1600 +1005120 =156300 . 2

Ответ. 31 декабря 2013 г. на счете окажется 156 300 руб.

Перейдем к случаю начисления сложных процентов.

Пример 13. В первый день каждого года, начиная с 1 января 2004 года, вкладчик помещает на свой счет в банке 100 000 руб. Расчет производится по схеме сложных процентов с годовой процентной ставкой 6 %. Какая сумма окажется на счете 31 декабря 2013 года?

Решение. На первую сумму, внесенную на счет, процентные деньги начисляются в течение 10 лет, поэтому к 31 декабря 2013 г. первая сумма превращается в сумму

F1 = 1000(1+0,06)10 = 179 084,77.

На вторую сумму, внесенную на счет, процентные деньги начисляются в течение 9 лет, и к 31 декабря 2013 г. она превращается в сумму

F2= 1000(1+0,06)9 = 168 947,9.

Третья внесенная на счет сумма превращается в сумму

F3 = 1000(1+0,06)8 = 159 384,81

и т.д. Таким образом, возникает убывающая геометрическая прогрессия F1, F2, … , F10 с первым членом 179 084,77 и знаменателем q = 1/1,06 = 0,9434, последний член которой

F10 = 100 000(1+0,06) = 106 000.

Сумма этой геометрической прогрессии

37

Ответ. 31 декабря 2013 г. на счете окажется 1 397 257,42 руб.

Определение. Наращенная сумма потока платежей – это сумма всех членов последова-

тельности платежей с начисленными на них процентами к концу срока ренты. Под современной величиной потока платежей понимают сумму всех его членов , дисконтированных ( приведенных) на некоторый момент времени, совпадающий с началом потока платежей или предшествующий ему.

Финансовая рента имеет следующие параметры:

член ренты – величина каждого отдельного платежа; период ренты – временной интервал между двумя соседними платежами,

срок ренты - время, измеренное от начала финансовой ренты до конца ее последнего периода; процентная ставка - ставка, используемая при наращении или дисконтировании платежей, образующих ренту.

Взависимости от продолжительности периода ренты делят на годовые и p - срочные, где p

–число выплат в году. По числу начислений процентов различают ренты с начислением 1 раз в году, m раз или непрерывно. Моменты начисления процентов могут не совпадать с моментами рентных платежей.

4.8.1. Формулы наращенной суммы. Обычная годовая рента

Пусть в конце каждого года в течение n лет на расчетный счет вносится по R руб., сложные проценты начисляются 1 раз в год по ставке r, тогда наращенная сумма в конце срока будет равна:

Пример 14. В течение трех лет на расчетный счет в конце каждого года поступает по 10 млн. руб., на которые один раз в год начисляются проценты по сложной годовой ставке 10 %. Требуется определить сумму на расчетном счете к концу указанного срока.

Решение. По формуле находим

FV =10 (1 +0,1)3 −1 = 33,1 млн. руб. 0,1

Годовая рента с начисление процентов m раз в году. Посмотрим, как усложнится фор-

мула, если предположить теперь, что платежи делают 1 раз в конце года, а проценты начисляются m раз в году. Это означает, что применяется каждый раз ставка rj / m,

где rj – номинальная ставка процентов. Тогда члены ренты с начисленными до конца срока процентами имеют вид

R(1+rj/m)m(n-1), R(1+rj/m)m(n-2), …, R

38

Если рассмотрим эту последовательность справа налево, то увидим, что перед нами опять геометрическая прогрессия, первым членом которой является R, знаменателем (1+rj/m)m, а число членов равно n. Сумма членов этой прогрессии и будет наращенной суммой ренты:

FV = R (1+rj / m)mn −1 . (1+rj / m)m −1

Пример 15. В течение трех лет на расчетный счет в конце каждого года поступает по 10 млн. руб., на которые ежеквартально (m = 4) начисляются проценты по сложной годовой ставке 10 %. Требуется определить сумму на расчетном счете к концу указанного срока.

Решение. По формуле находим

FV = 10[(1+0,1/4)3*4-1] / [1+0,1/4)4-1] = 33,222 млн. руб.

Рента р - срочная, m =1. Найдем наращенную сумму при условии, что рента выплачивается p раз в году равными платежами, а проценты начисляются 1 раз в конце года. Если R - годовая сумма платежей, то размер отдельного платежа составляет R/p. Тогда наращенная сумма рассматриваемой ренты равна:

Пример 16. В течение трех лет на расчетный счет в конце каждого квартала поступают платежи равными долями из расчета 10 млн. руб. в год (т.е. по 10/4 млн. руб. в квартал), на которые в конце года начисляются проценты по сложной ставке 10% годовых. Требуется определить сумму на расчетном счете к концу указанного срока.

Решение. По формуле находим

FV = (10/4)[(1+0,1)3-1] / [(1+0,1)1/4-1] = 34,317 млн. руб.

Рента р - срочная, р = m. В контрактах часто начисление процентов и поступление платежа совпадают по времени, т.е. p = m. Тогда для получения наращенной суммы можно воспользоваться формулой:

Пример 17. В течение трех лет на расчетный счет в конце каждого квартала поступают платежи равными долями из расчета 10 млн. руб. в год (т.е. по 10/4 млн.руб. в квартал ) , на которые ежеквартально начисляются проценты по сложной ставке 10% годовых . Требуется определить сумму на расчетном счете к концу указанного срока .

Решение. По формуле находим

FV = 10[(1+0,1/4)3*4-1] / 0,1 = 34,489 млн. руб.

39

Рента р – срочная, р ≥ 1, m ≥ 1. Рассмотрим самый общий случай p - срочной ренты с начислением процентов m раз в году, причем возможно p ≠ m . В результате получаем наращенную сумму:

Пример 18. В течение трех лет на расчетный счет в конце каждого квартала поступают платежи (р =4) равными долями из расчета 10 млн. руб. в год (т.е. по 10/4 млн.руб. в квартал ), на которые ежемесячно (m=12) начисляются проценты по сложной ставке 10 % годовых. Требуется определить сумму на расчетном счете к концу указанного срока.

Решение. По формуле находим

FV = (10/4)[(1+0,10/4)3*4-1] / [(1+0,10/4)12/4-1] = 34,5296 млн. руб.

4.8.2. Формулы современной величины. Обычная годовая рента

Пусть размер годового платежа равен R , процентная ставка r , проценты начисляются 1 раз в конце года , срок ренты n . Тогда дисконтированная величина первого платежа равна:

R 1 +1 r =Rv.

Приведенная к началу ренты величина второго платежа равна Rv2 и т. д. В итоге приведенные величины образуют геометрическую прогрессию: Rv, Rv2,…, Rvn , сумма которой

где anr = (1 – (1+r)-n)/r - коэффициент приведения ренты, значения которого можно пред-

ставить в табличном виде.

Пример 19. В течение трех лет на расчетный счет в конце каждого года поступает по 10 млн. руб. Ежегодное дисконтирование производится по сложной ставке 10 % годовых. Определить современную стоимость ренты.

Решение. По формуле

A = 10[1-(1+0,1)-3] / 0,1 = 24,868 млн. руб.

Формула для расчета современной величины ренты в самом общем случае для произвольных значений p и m , где p ≥ 1, m ≥ 1 вычисляется:

A =R 1 −(1 + rj / m)−mn p((1 + rj / m)m / p −1)

4.8.3. Зависимость между современной величиной и наращенной суммой ренты

Пусть A- современная величина годовой ренты постнумерандо, а FV - ее наращенная стоимость к концу срока n , p= 1, m= 1 .Наращение процентов на сумму A за n лет дает сумму, равную

FV:

40

Отсюда же следует , что дисконтирование FV дает A:

FV vn = A,

а коэффициенты дисконтирования и наращения ренты связаны соотношениями

anr (1+ r)n = snr ;

snr vn =anr .

4.8.4. Определение параметров финансовой ренты

Иногда при разработке контрактов возникает необходимость определить по заданной наращенной сумме ренты FV или ее современной стоимости. A остальные параметры ренты :R ,n ,r ,p, m .Такие параметры, как m и p, обычно задаются по согласию двух подписывающих сторон. Остаются параметры R , n, r . Два из них задаются, а третий рассчитывается.

Определение размера ежегодной суммы платежа. В зависимости от того, какая обоб-

щающая характеристика постоянной ренты задана - FV или A , возможны два следующих варианта расчета:

Определение срока постоянной ренты. Разрешая исходные формулы для FV и A относительно срока n , получаем соответствующие выражения:

Последнее выражение для n , очевидно, имеет смысл только при R> Ar .

4.9.Вопросы и задачи для проверки усвоения пройденного материала

1.Дать определение аннуитета.

2.По каким формулам вычисляются аннуитеты, если на них начисляются процентные

деньги.

3.Какие схемы погашения ссуд Вы знаете, в чем их сущность?

4.В чем суть потребительских кредитов?

5.Что такое финансовые ренты, какие финансовые ренты бывают?

6.Что называется наращенной суммой потока платежей, как она вычисляется?

7.Как вычисляется современная величина потока платежей?

8.Задачи для самостоятельного решения.

Задача 1. .Покупатель обратился в банк с просьбой о предоставлении кредита на покупку ноутбука стоимостью 36 000 руб. Банк предоставил покупателю потребительский кредит на срок 2 года на основе годовой процентной ставки 20 % с ежемесячными погашениями постнумерандо. Какую сумму денег покупатель должен ежемесячно перечислять банку, если при расчете применяется схема:

1)простых процентов?

2)сложных процентов?

Задача 2. Заем 200 000 долл., предоставленный на срок 5 лет с годовой процентной ставкой 15 % , погашается одинаковыми аннуитетами постнумерандо. Кредитор по такой же схеме рассчи-

41

тывает процентные деньги за пользование каждым аннуитетом с момента его получения и до срока окончания займа, которые идут в счет погашения займа. Найти значения аннуитетов, если при расчете применяется схема :

1)простых процентов?

2)сложных процентов?

Задача 3.Заем в сумме 5 000 000 долл. Погашается в течение 10 лет аннуитетами постнумерандо, причем выплаты долга от года к году:

1)увеличиваются на 25 000 долл.,

2)уменьшаются на 25 000 долл.

Задача 4. В первый день каждого месяца, начиная с 1 января 2005 год , вкладчик помещает на свой счет в банке 2 000 руб. Расчет производится по схеме простых процентов с годовой процентной ставкой 8 % и помесячным начислением процентных денег, причем год рассматривается состоящим из 12 месяцев по 30 дней . Какая сумма окажется на счете 31 декабря 2010 г.?

Задача 5. В фонд ежегодно постнумерандо вносится по 10 000 руб. в течение 20 лет, на которые начисляются сложные проценты 10 % годовых один раз в году . Определить наращенную сумму на конец срока .

Задача 6. В фонд ежегодно постнумерандо вносится по 10 000 руб. в течение 20 лет, на которые начисляются сложные проценты 10% годовых ежеквартально. Определить наращенную сумму на конец срока.

Задача 7. В фонд ежегодно вносится по 10 000 руб. в течение 20 лет. Платежи производят равными долями в конце каждого квартала. Сложные проценты по ставке 10 % годовых начисляются один раз в конце года . Определить наращенную сумму на конец срока .

Задача 8. В фонд ежегодно вносится по 10 000 руб. в течение 20 лет. Платежи производят равными долями в конце каждого квартала. Сложные проценты по ставке 10 % годовых начисляются ежеквартально. Определить наращенную сумму на конец срока.

Задача 9. В фонд ежегодно вносится по 10 000 руб. в течение 20 лет. Платежи производят равными долями в конце каждого квартала. Сложные проценты по ставке 10 % годовых начисляются ежемесячно. Определить наращенную сумму на конец срока.

Задача 10. В течение 20 лет на расчетный счет в конце каждого года поступает по 10 000 руб. Ежегодное дисконтирование производится по сложной ставке 10 % годовых. Определить современную стоимость ренты.

42