Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Белорусский национальный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

opt1-2[1]

.pdf

Скачиваний:

Добавлен:

26.03.2016

Размер:

247.22 Кб

Скачать

☆

1.2.Энергия и поток энергии электромагнитного поля.

1.2.1.Изменение энергии в объеме. Уравнение неразрывности.

Энергия электрического и магнитного полей нами уже определялась в разделе “Электромагнетизм” соотношениями

r r

Wэл =

∫EDdV

Wэл =

∫EdDdV

8π

или более общими

4π

(1.2.1)

Wмагн =

∫HBdV

Wмагн =

∫HdBdV

8π

4π

Под действием электрических и магнитных сил может совершаться работа. Поэтому, записывая закон сохранения энергии для электромагнитного поля, необходимо включать и эту работу тоже.

Пусть среда, в которой возбуждается электромагнитное поле и токи неподвижна. Тогда в единице объема возбуждается энергия за счет работы внешних сил – энергия электромагнитного поля и энергия

тока:	1	r r r r	r r

δA =		(HdB + EdD)+ (j ,E)dt		(1.2.2)
	4π

Последнее слагаемое в (1.2.2) описывает Джоулево тепло. Считаем для простоты, что других превращений энергии в этом объеме нет. Эта работа δА идет на приращение внутренней энергии за вычетом тепла, уходящего из единицы объема среды вследствие теплопроводности. Если теплопроводность равна 0, то весь запас внутренней энергии пополняется работой δА.

Пусть u - внутренняя энергия единицы объема. Тогда ее приращение равно работе внешних сил:

δA = du = 41π (ErdDr + HrdBr)+ rjErdt

Или, разделив на dt, имеем в дифференциальной форме и интегральной (для конечного объема V) формах, соответственно:

∂U ∂t

∂u

∂D

∂B

+ H

+ jE

∂t

4π

∂t

∂

∫udV =

∂D r ∂B

+ H

∂t

∫ E

∂t

dV + ∫

4πV

∂t

rr jEdV

(1.2.3)

(1.2.4)

Под u понимается плотность всей внутренней энергии, а не только ее электромагнитная часть. Поэтому уравнение (1.2.3) справедливо для любых сред, в том числе ферромагнитных и сегнетоэлектрических. Оно

учитывает не только джоулево тепло ( jE ), но и тепло ферромагнитного и диэлектрического гистерезиса.

1 ∂D

4π r

1 ∂B

Преобразуем (1.2.3), вспомнив уравнения Максвелла

= rotH и

−

= rotE :

∂t

∂u 1 r

r r

1 r ∂B

1 ∂D

1 r ∂B c

c r

∂D

+ E j +

(E,rotH )−

(H ,rotE)

∂t

4π

∂t

4π

∂t

= E,

4π ∂t

+ j

4π

∂t

4π

Далее, используя векторное тождество ErotH − HrotE = −div[E,H ], получаем:

∂u

div[Er,Hr]= 0

(1.2.5)

Введем вектор

∂t

4π

Sr ≡

[Er,Hr

(1.2.6)

4π

тогда получаем уравнение (1.2.5) типа уравнения неразрывности (вспомним закон сохранения плотности

вероятности или закон сохранения заряда	∂ρ	+ divrj = 0 ):
	∂t	∂u	+ divSr = 0
		∂u	+ divSr = 0	(1.2.7)
		∂t

По аналогии с другими законамиr сохранения заключаем, что поскольку имеем изменение плотности

энергии во времени, то вектор S играет роль плотности потока электромагнитной энергии. Смысл уравнения становится более понятным, если записать его в интегральной форме. Пользуясь (1.2.4) и (1.2.6), имеем:

∂U	r	∂U	r r	= 0	(1.2.8)
∂t	+ ∫divSdV =	∂t	+ ∫Sds	= 0	(1.2.8)
∂t	V	∂t

То есть приращение внутренней энергии в объеме V происходит за счет электромагнитной энергии,

втекающей в этот объем из окружающего пространства через поверхность s.

------------------------------------------------------------------------------------------------------

Примечание 1. Различные выражения закона сохранения энергии.

1). Если теплопроводность отлична от 0, то к потоку электромагнитной энергии добавится плотность потока

тепла.
2). Электромагнитная часть энергии определяется				соотношением			dW = ∫dwdV ,	где приращение
							V
			1		r r	r	r
плотности электромагнитной энергии равно dw =			1		(EdD	+ HdB). Тогда, разделяя полную энергию
плотности электромагнитной энергии равно dw =		4π			(EdD	+ HdB). Тогда, разделяя полную энергию
		4π
U на электромагнитную энергию W и джоулево					тепло	Pdt = σE 2 dt = jEdt ,		можно записать
выражение для мощности, выделяемой в объеме V из-за токов проводимости:
P = −	∂W				r r			(1.2.9)
P = −	∂t			− ∫Sds				(1.2.9)
	∂t				s

Эта мощность равна уменьшению энергии электромагнитного поля и потоку энергии через поверхность объема. Если энергия электромагнитного поля не изменяется во времени (стационарный случай), то

мощность равна нулю ∂W	∂t	= 0 и вся производимая работа в замкнутом объеме совершается за счет

энергии электромагнитного поля, проникающую через поверхность, ограничивающую объем.
3). Если рассматриваем вакуум		или диэлектрик,	то плотность тока проводимости	j = 0 и мощность
выделяемого джоулева тепла		P = 0 и в закон сохранения энергии входят только электромагнитные
величины:		∂W	r r
				(1.2.10)
		∂t	+ ∫Sds = 0
			s
---------------------------------------------------------------------------------------------------------------------------------

Вектор плотности потока электромагнитной энергии S называется вектором Пойнтинга. Иногда его называют вектором Умова – Пойнтинга. Умов ввел понятие плотности потока энергии для упругих сред и

вязких жидкостей в 1874 г. Пойнтинг ввел вектор S для электромагнитного поля в 1885 г. (Джон Генри Пойнтинг, английский физик, 1852–1914; Николай Алексеевич Умов, русский физик, 1846–1915). Размерность вектора Пойнтинга:

[S ]= энергия/время площадь (в системе единиц Гаусса [S ]= смЭрг2 с ).

Отметим, что кроме простоты выражение Sr = 4cπ [Er,Hr]отличается большой общностью, так как вектор

Пойнтинга выражается только через напряженности полей E и H и не содержит никаких величин, характеризующих индивидуальные свойства среды, в которой течет электромагнитная энергия.

-------------------------------------------------------------------------------------------------------------------------------------------

Приложение 1.

Другой вариант рассмотрения пункта 1.2.1. (более частное рассмотрение). Энергия и поток энергии электромагнитного поля.

Если принять, что энергия электромагнитного поля может быть локализована в пространстве, то её объемная плотность в произвольном месте поля определяется выражением

r r

w =

(DE + BH )=

(εE 2 +µH 2 ).

8π

Рассмотрим теперь изменение во времени энергии поля W , заключенной в объеме V , ограниченном

неподвижной поверхностью s .

(DE + BH )dV

= ∫∂wdV .

∂W = ∂ 1 ∫

r r

∂t

8π

V ∂t

Если характеристики среды ε и µ не меняются со временем, то

∂w

∂E

∂H

∂D

+µH

+ H

∂B

∂t

εE

∂t

4π

∂t

4π

Подставляя сюда из уравнений Максвелла

∂D

= crotHr − 4πrj

∂B

= −crotEr, имеем

∂t

∂w

= −rjEr +

(ErrotHr − HrrotEr),

4π

∂t

или в силу векторного тождества

ErotH − HrotE = −div[E,H ]:

∂w

= −rjEr −

div[Er

,Hr].

∂t

4π

Если среда неподвижна и мы пренебрегаем теплом, уходящим из среды вследствие теплопроводности (положив последнюю равной нулю), то изменение внутренней энергии u единицы объема среды происходит за счет изменения энергии электромагнитного поля и работы, совершаемой электрическим

полем E над токами проводимости j

∂∂ut = ∂∂wt + rjEr .

Введем обозначение Sr = 4cπ [Er,Hr]. Тогда

∂∂ut + divSr = 0 .

Для понимания физической смысла этого уравнения сравним его с уравнением непрерывности – законом сохранения заряда

∂∂ρt + divrj = 0 .

Использование формальной аналогии позволяет сделать вывод, что энергия течет в пространстве подобно

некоторой жидкости, причем вектор S приобретает смысл плотности потока электромагнитной энергии. В интегральной форме это уравнение принимает вид

	Sr		∂U	+ ∫Srdsr = 0 ,
			∂t
V		где U - внутренняя энергия объема, ограниченного поверхностью s . В
	nr	такой форме уравнение означает, что приращение внутренней энергии U в
s		объеме V происходит за счет электромагнитной энергии, втекающей в этот
		объем из окружающего пространства через поверхность s .
		Представление о течении энергии сохраняется также при учете
теплопроводности,	но к	плотности потока электромагнитной энергии в этом случае следует добавить

4
плотность потока тепла. Таким образом, уравнение	∂u	+ divSr = 0 выражает закон сохранения энергии
	∂t

в электродинамике и носит название теоремы Умова – Пойнтинга.

1.2.2. Поток энергии в плоской электромагнитной волне.

Итак, плотность потока электромагнитной энергии задается вектором Пойнтинга (1.2.6). Ранее для вектора напряженности магнитного поля в плоской электромагнитной волне мы получили (см. §1.1.

формула (1.1.21))

Hr = µωc [kr,Er].

Подставим H в выражение для вектора Пойнтинга, и, вспоминая поперечность электромагнитной волны, а также связь между модулями векторов напряженности электрического и магнитного поля в этой волне

(1.1.25)	εE = µH , получаем:	0
		0

Sr =

[Er[kr,Er]]=

(krE 2 − Er

(kr,Er))= c2 E 2 k

= c2 H 2 k

= c2 EH

4πµω

4π µ

4π ε ω

4π εµ ω

Плотность энергии в электромагнитной волне, распространяющейся в однородной и изотропной среде,

равна

w =

(εE 2

+µH 2 ).

(1.2.11)

8π

И с учетом

εE =

µH , имеем для плотности энергии:

w =

εE 2

(1.2.12)

4π

Тогда можно записать вектор Пойнтинга в следующем виде (т.к. фазовая скорость

= v ):

c2 E 2 r

v 2

k =

= wv ,

(1.2.13)

4π

µω

εµω

Интерпретация этого соотношения, таким образом, довольно проста: электромагнитная волна переносит энергию в направлении своего распространения:

S = wvr

(1.2.14)

1.2.3. Другие примеры.

1. Выделение джоулева тепла в проводнике.

Пусть по цилиндрическому проводнику радиусом r течет

постоянный

ток

I .

Магнитное

поле тока

на

поверхности

проводника

равно

(из

теоремы

циркуляции

H 2πr =

4π

πr 2

j ):

H =

2πjr

(1.2.15)

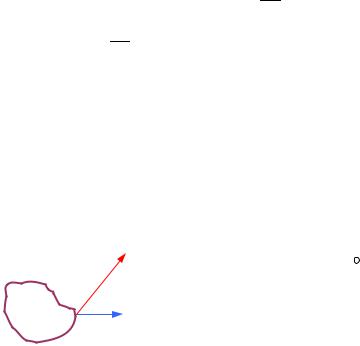
а его силовые линии представляют собой концентрические

окружности. Электрическое поле E параллельно оси провода (см рисунок). Поэтому вектор Пойнтинга S направлен внутрь проводника нормально к его боковой поверхности. Следовательно, электромагнитная

энергия втекает из окружающего пространства внутрь проводника. Сравним её с количеством теплоты, выделяющимся в проводнике при протекании тока. Поток электромагнитной энергии сквозь боковую поверхность участка проводника длиной l равен:

S 2πrl =	c	EH 2πrl = πr 2 ljE =VjE .	(1.2.16)
	4π

Здесь вместо напряженности магнитного поля подставлено выражение (1.2.15), V - объем участка проводника. Таким образом, поток электромагнитной энергии, поступающей в проводник извне, целиком превращается в джоулево тепло.

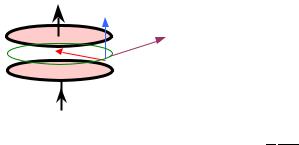
2. Зарядка конденсатора.

циркуляции вектора H

конденсатора равен

находим

Пусть плоский конденсатор имеет круглые обкладки радиусом r , находящиеся на расстоянии h друг от друга. Пренебрегая краевыми эффектами, найдем поток электромагнитной энергии, втекающей в конденсатор через его боковую “поверхность” (именно там вектор Пойнтинга направлен внутрь конденсатора). На этой “поверхности” имеется меняющееся во времени электрическое поле

E и вызванное его изменением магнитное поле H . По теореме о

H 2πr = 1c ∂∂Dt πr 2 . Тогда поток электромагнитной энергии внутрь

S 2πrh =

EH 2πrh =

∂D

hπr 2 =

∂D

(1.2.17)

4π

∂t

Таким образом, за время dt приращение энергий конденсатора составит (если D = εE ):

dW =

EdD =

d (εE 2V )=

d (EDV ).

(1.2.18)

4π

8π

Проинтегрировав это выражение, мы получаем формулу для энергии заряженного конденсатора.

Соседние файлы в папке В.К. Иванов. Волновая оптика

#
26.03.2016285.04 Кб38opt1-1[1].pdf
#
26.03.2016247.22 Кб39opt1-2[1].pdf
#
26.03.2016204.42 Кб38opt1-3[1].pdf
#
26.03.2016249.13 Кб41opt1-4[1].pdf
#
26.03.2016199 Кб42opt1-5[1].pdf
#
26.03.2016190.58 Кб44opt1-6[1].pdf
#
26.03.2016180.15 Кб40opt1-7[1].pdf