1.4. Понятие связи и ее реакции

Все тела можно разделить на две группы свободные и несвободные.

Тело называют свободным, если оно может получать перемещение в лю-

бом направлении (свободно падающий камень).

Тело называют несвободным, если оно не может получать перемещения

хотя бы в одном направлении (шарик на нити не может удалиться от точки

подвеса).

Физические тела, ограничивающие свободу других тел, называют механи-

ческими связями, или просто связями.

Сила, с которой связь действует на рассматриваемый объект, называется

реакцией связи, или реактивной силой.

У

В подавляющем большинстве тела являются несвободными. Это значит,

что связей имеется бесчисленное множество. Однако их можноТобъединить в

группы (типы) по различным признакам.

NB

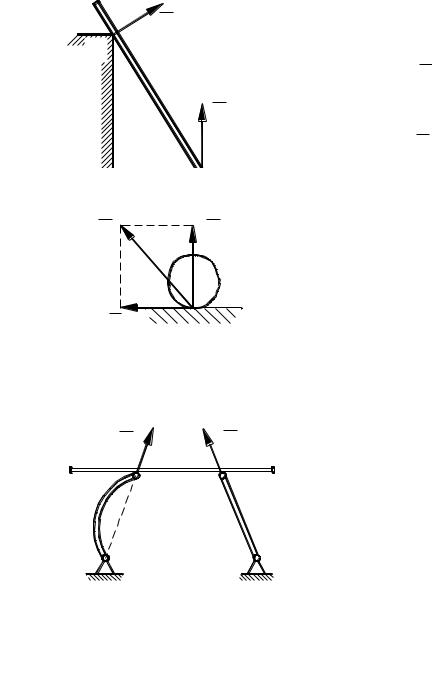
Гладкая поверхность. СвязьНограничивает пе-

ремещение тела лишь в одном направлении. Ее реак-

B

ция совпадает с нормалью к поверхности связи в

Б

точке касания (см.

N A ). Если в точке касания к связи

нельзя

нормаль (край стены, острие), то ре-

NA

й

акцию нап авляют по нормали к поверхности каса-

ющегося тела (см.

NB ).

A

и

провести

R

N

оНегладкая (шероховатая) поверхность. В

э ом случае кроме нормальной реакции имеется

т

и

также составляющая в касательной плоскости

(силы трения).

Fтр

з

Гибкаяосвязь (трос, канат, ремень, цепь, нить). Такая связь считается неве-

сомой, н растяжимой, гибкой. Ее реакция всегда направлена вдоль связи.

п

N1

N2

Невесомый стержень. Такой стержень

е

является промежуточным звеном между телом и

Р

опорой. Он соединен с ними посредством шар-

ниров без трения, и его реакция всегда направ-

лена вдоль прямой, соединяющей шарниры (см.

N1

и N2 ).

Шарнирные опоры. Различают три случая таких опор.

YA

Тело соединено цилиндрическим шарниром с не-

XA

подвижной опорой (шарнирно-неподвижная опора).

A

Соединение позволяет телу поворачиваться вокруг оси

шарнира. Реакция в шарнире перпендикулярна к его

оси и при решении задач раскладывается обычно на

две перпендикулярные составляющие.

RB

RB

RB

Тело

соединено

цилиндрическим

шарниром с опорой, которая может пере-

B

B

B

мещаться по другой опорной поверхности

(шарнирно-подвижная опора). Если эта

поверхность – гладкая, то реакцияУнаправ-

лена по нормали к опорной поверхности.

Тело соединено сферическим шарниром с неподвижной опоройТ. Соеди-

нение позволяет телу поворачиваться вокруг центра шарнира. Реакция в шар-

нире может иметь любое направление и при решении задач обычно расклады-

вается на три перпендикулярные составляющие.

Н

БZA

а)

z

б)

RA

й

RA

y

и

A

YA

x

р

XA

Gt

о

Петля, завеса, ц л ндр ческий подшипник. Соединение позволяет те-

лу поворачиваться вокруг

петли и перемещается в отверстии. Для упро-

центра

щения расчетов пр н мают, что данный вид связи ограничивает только линей-

ные перемещения в плоскости перпендикулярной оси вращения вала. Опору

считают беск

у кой и моменты реакций не учитывают.

з

Реакция лежит в плоскости и при решении задач обычно раскладываются

на

ер ендикулярные составляющие.

нечно

п

две

Р

10

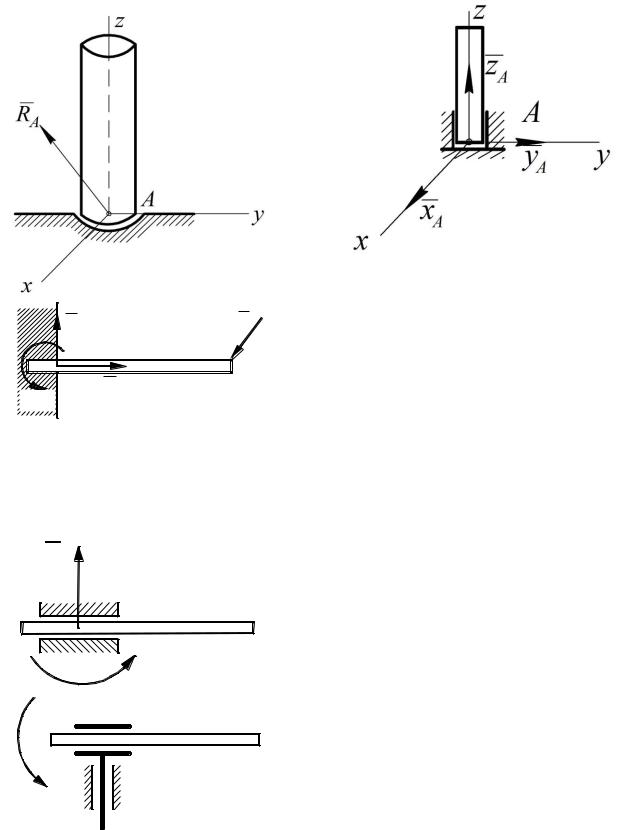
Подпятник. Связь позволяет телу поворачиваться, т.е. ограничивает пе-

ремещение вала по осям координат, не препятствуя его поворотам относи-

тельно осей координат. Реакцию в подпятнике при решении задач обычно рас-

кладывают на три перпендикулярные составляющие.

У

Т

Н

Б

YA

P

Жесткая заделка. Если тело со связью

соед нено жестко (не допускаются никакие

й

пе емещен я), то такое соединение назы-

вают жесткой заделкой, или защемлением

MA

XA

(к нецбалки в кирпичной или бетонной

кладке, конец столба в земле). Реакция

р

такой связи состоит из силы и пары. Силу раскладывают на две перпендику-

лярные составляющие, а пару сил прикладывают к защемленному концу,

направляя ее по ходу

о

про ив хода стрелки часов (для плоской системы

т

сил). Или на три перпенд кулярные составляющие и на три пары сил вокруг

трех перпендикулярных осей (для пространственной системы сил).

ли

Скользящая заделка. Связь ограничи-

RА

з

вает линейное перемещение тела в одном

о

направлении и не позволяет телу поворачи-

ваться вокруг опоры. Ее реакция расклады-

п

вается на силу RA , которая направлена по

нормали к заделке и на пару сил прило-

е

МА

женных к телу с моментом M A .

Р

Двойная скользящая заделка. Связь

препятствует повороту тела. Ее реакция

представляет собой пару сил приложенных

МА

к телу с моментом M A .

11