
1-41
.pdf
10. статический и кинематичский методы построение линий влияния.
1.Статический метод построения ЛВ:
Зав-ти для опр-ия опорных реакций при перемещении ед-ой силы по балке получаем из ур-ий равновесия балки. Верт-ую р-цию опр-им из уравнения ΣY=0 => RA=1 по всей длине.
Момент определим из ур-ия: ΣМА=0, -MRA+1XFA=0;
MRA=XFA. ИМ и поперечную силу в т.К опр-им из урия равновесия правой части, когда сила справка: Мк пр=-1ХFK (при ХFK=0; Мк=0 при XFK=c MК=-с); Qк
пр=+1.
Когда сила слева рассматриваем правую часть и получаем, что на участке слева Мк=0, Qк=0. Для построения ЛВ в многопролетной балке требуется сначала построить ЛВ в простой балке, к которой рассматриваемое усилие. Ордината ЛВ в шарнире , соединяющим главную балку с второстепенной, явлся уже известной. При расположении подвижной нагрузки над опорой давление на ниже
расположенную балку не передается 2.Кинематический метод построения ЛВ: он основан на принципе возможных
перемещений, согласно к-му для находящейся в равновесии системы сумма работ всех сил на любых возможных бесконечно малых перемещениях = 0. Для построения ЛВ этим методом необходимо отбросить связь в к-ой возникает это усилие, после чего полученному механизму по направлению усилия в отброшенной связи задается перемещение равное единице. Полученный график усилия и будет представлять собой ЛВ рассматриваемого усилия.
Рассмотрим двухопорную балку. Отбросим правую опору, заменив ее действием реакцией
RB. За возможные перемещения примем перемещения, вызванные поворотом балки |
|
|
вокруг точки А на угол θ. Запишем сумму работ сил, действующих на систему: |
|
|
-F∆c+RB∆B=0 => RB=F∆c/∆B |
. Т.О. числитель-ф-ция, соот-щая |
эрюре |
с будет изм-ся как ф-ция аргумента Х |
||
возможных вертикальных перемещений, а |
знаменатель явл-ся масштабным |
коэф- |
ом,приравняв его к 1, получим=> RB= с. |
|
|
Сл-но очертание линии влияния RB (г) соот-ет эпюре возможных |
||
перемещений балки (в). Перемещение точек С и В можно |
|
|
выразить через угол поворота θ: ∆c= xtgθ=xθ; ∆B=l tgθ=lθ |
|
|
Подставляя их в выражение для RB, получим: RB= x/l. Для построения ЛВ изгибающего момента в сечении К рассматриваемой балки введем шарнир в этом сечении (д). Сумма работ сил и моментов опр-ся: -F∆c+Mkφ=0, где φ-угол взаимного поворота торцевых сечений эл-ов примыкающих к шарниру(ж)=> при F=1: Mk=∆c/φ Приняв φ=1 получим, что искомая ЛВ ИМ в сеч. К совпадает с эпюрой возможных перемещений балки(ж.)
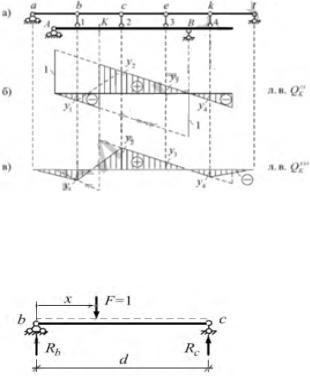
11.Линии влияния при узловой передаче нагрузки.
Нагрузка передается на сооружение не непосредственно, а через дополнительные устройства, к-е представлены в виде двухопорных балок-передаточные. Сооружения, на к-е передается нагрузка через передаточные устройства-основные или главные. Передаточные балки передают нагрузки на главные только в опр-ых точках-узлах. При узловой передаче нагрузки на уч-ах между узлами л.в усилий всегда будут линейными. Рассм. л.в. поперечной силы в сеч-и К балки АВ при движении груза по этой балке (рис. 3.12,а,б). Пусть
нагр-а на балку АВ передается посредством системы передаточных балок.
Выделим уч-к между узлами b и с. При расположении силы в точке b или с, т. е. над опорами передаточной балки be, она через опорные стержни будет полностью передаваться на главную балку. Значит, положение силы в точке b или с на передаточных балках эквивалентно ее положению в точках 1 или 2 на главной балке. ординаты yi и у2 л.в. Qk, полученные при непосредственном нагружении главной балки, будут справедливы и при узловой передаче нагрузки. При движ-и еди-
ничной силы по балке be ее опорные реакции (рис. 3.13) равны: Rb = (d-x)/x ; dRc = x/d . Попер-ая сила в сечении К от действия сил, передаваемых на главную балку посредством опорных стержней в точках 1 и 2: Qk=RbУ1+RcУ2=(d-x)/d*У1 + x/d *У2= У1+(y1-y2)/d* x. Полученное выражение п. с. ур-ие прямой на участке be. Следовательно, л. в. Qk на участках между узлами является прямолинейной. Т. о., для построения л. в. усилия при узловой
передаче нагрузки необходимо сначала построить л. в. рассматриваемого усилия при непосредственном загружении сооружения. Затем необходимо зафиксировать ординаты этой л. в. под узлами и соединить их прямыми линиями.
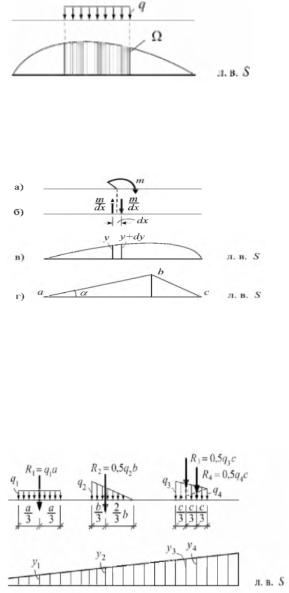
12.Определение усилий по линиям влияния.
Ордината y i л.в усилия S п. с. знач-е этого усилия при расположении единичной силы над этой ординатой. Если над ординатой y, будет не единичная сила, а сила F, то усилие от ее действия будет в F раз больше. То есть усилие равно: S = F yi. усилие S, вызванное системой сосредоточенных сил равно: S = F1 У1 + F2 У2 + - + Fn y n = ∑Fiyi, Усилие S равно
произведению интенсивности нагрузки q на площадь Q л. в. усилия под этой нагрузкой. Для вычисления усилия по л.в. от сосредоточенного момента, представим этот момент в виде пары сил, действующих в окрестности точки приложения момента. Плечо пары сил примем бесконеч-
но малым (dx), тогда каждая из сил будет равна m /dx. Для вычисления усилия воспользу-
емся выражением: m m dy, S = -m/dx* y + m/dx* (y + dy) =mdy/dx= my’
Т.о, усилие S от действия сосредоточенного момента вычисляется по л.в этого усилия как произведение момента на значение первой производной от фун-и влияния усилия в точке приложения момента. При этом сосредоточенный момент принимается полным,
если он действует по часовой стрелке. На линейном участке л.в. производная от фун-и влияния усилия равна тангенсу угла наклона участка л.в усилия по отношению к базовой оси. В этом случае усилие от действия сосредоточенного момента можно вычислить по формуле: S= m*tga. Для стат-ки опр-ых систем, у к-ых л.в. явл-ся кусочно-линейными, общее выражение для оприя усилий от действия сосредоточенных сил, равномер-
но распределённых нагрузок и сосредоточенных моментов имеет вид: S = ∑Fiyi+
+∑q jΩj +∑mk tg ak, (i=1, n; j=1, s; к=1, t), где n, s, t - число, соответственно, сосредоточенных сил Fi, равномерно распределённых нагрузок qj и сосредоточенных моментов mk. Важным при опр-нии усилий от внешних нагрузок явл-ся след-е св-во прямолинейного участка л.в: на прямолинейном участке л. в. усилие от системы вертикальных сил м.б. определено произведением равнодействующей этой системы сил на ординату л. в. под равнодействующей. Это св-во упрощает опр-ие усилий от действия любых нагрузок, действующих на прямолинейных участках л.в, при условии, что можно легко найти равно-
действующие этих нагрузок и точки их приложения. Так, в случае равномерно распределённой нагрузки ее равнодействующая = произведению интенсивности нагрузки на длину участка и приложена в середине этого участка. Распределённую нагрузку, имеющую форму трапеции, следует разбивать на равномерно распределённую и треугольную нагрузки. Либо на две нагрузки, распределенные по форме треугольников:
S = (q1*a)У1+(0,5q2b)У2 + (0,5q3c )y3 + (0,5 q4c) y4
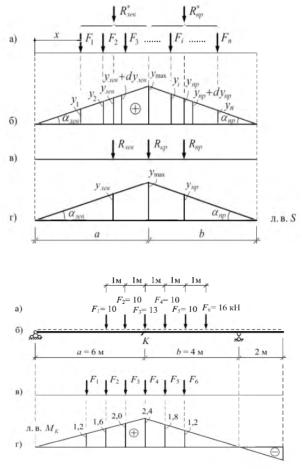
13.Определение наиболее невыгодного положения подвижных нагрузок по л. в.
Наиболее невыгодным положением на сооружении подвижной нагрузки наз-ся такое положение, при к-ом рассматриваемое усилие достигает экстремального знач-я.
1. При действии на сооружение одной подвижной силы расчетному усилию будет соответствовать положение этой силы над наибольшей («+» или «-») ординатой л.в.
2. При действии на сооружение связанной системы сосредоточенных сил, расст-е между к-ми при их движ-ии не меняется, усилие опр-ся: S=∑Fiyi
Рассмотрим действие такой нагрузки на треугольном участке л. в. Примем, что система связанных сил движется слева направо. Положение поезда хар-ся абсциссой x.
Все силы можно разделить на 2 группы: -распол-ые слева от вершины л. в. (Fiлев), и - силы, распол-ые справа от вершины л. в. (Fk npав ). Каждую из этих групп можно привести к равнодействующим Rлев* и R*прав. Тогда выражение для усилия S:
S=ΣFiлев*Yiлев+ΣFkпрYk пр= R*лев Yлев+R*пр Yпр, где у лев, у пр - ординаты л.в. под равнодействующими. В состав равнодействующих следует включать только те грузы, к-ые находятся на соответствующем участке л.в.
Переместив поезд сил на бесконечно малую величину d x , найдемприращение усилия в виде: dS= R*лев dyлев+R*пр dyпр. Разделив на dx, получим выражение для первой производной усилия по переменной x:dS/dx=R*лев dyлев/dx+R*пр dyпр/dx
учитывая dyлев/dx=tgaлев, dyпр/dx=-tgaпр, полу-
чим dS/dx=R*лев tgaлев- R*пр tgaпр
условие для опр-ия невыгодного расположения нагрузки в виде 2-х неравенств: система
(Rлев+Fкр) tgaлев >= Rпр tgaпр; Rлев tgaлев<= (Rпр+Fкр) tgaпр
Первое неравенство-когда критическая сила находится слева от вершины л. в., а второе - когда критическая сила перешла через вершину. Учитывая, что tgaлев = ymax/ а и tgaпр = ymax /b неравенства, после сокращения на ymax: система (Rлев+Fкр)/а >=Rпр/b, Rлев/a<= (Rпр+Fкр)/b. Опр-ие критического груза в соответствии с условием сводится к пробным установкам поезда сил, при к-ых одна из сил, предполагаемая критической, располагается над вершиной л.в. Попытки повторяются до тех пор, пока не будут выполняться оба неравенства.
14.Матрицы влияния усилий в простых и многопролётных балках
15. Связь понятий «линия влияния» и «матрица влияния»
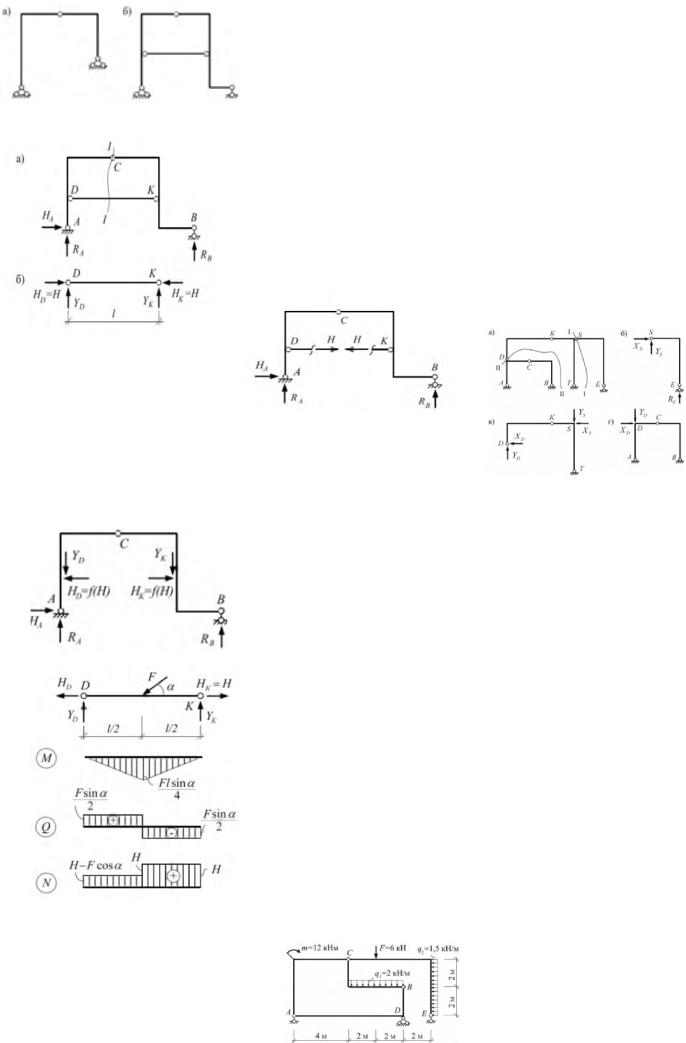
16. Расчёт трёхшарнирных и составных рам. |
|
Трехшарнирная рама п. с. два диска в виде ломаных стержней, соединенных между собой |
|
шарниром, при этом каждый из дисков опирается на шар- |
|
нирно неподвижные опоры. Если в трехшарнирной раме |
|
затяжка не нагружена, то ее следует рассматривать как |
|
связь первого вида, в которой может возникнуть только |
|
продольная сила. Усилие Н в затяжке DK опр-ся из ур -ия |
|
равновесия левой или правой части рамы, отделяемой се- |
|
чением, проходящим через ключевой шарнир и затяжку. |
|
Тогда для рамы можно принять следующий порядок расчета. |
|
1.Опр-ем опорные реакции: ΣМА=0 =>Rвб, ΣМв=0=>RA, |
|
ΣХ=0 =>НА. |
|
2. Рассматривая, например, равновесие правой части рамы, из |
|
ур-ия ∑Мправ с= 0 находим Н. Для проверки применяем |
|
условие равновесия левой части рамы: ∑М левС= 0. |
|
Для трехшарнирной рамы с нагруженной затяжкой, послед- |
|
нюю можно рассматривать как шарнирно опертую балку . |
|
Порядок расчета рамы сводится к следующему: |
|
1. Внешние опорные реакции Rа, Hа и Rв опр-ются так же, |
|
как и для трехшарнирной рамы |
|
с ненагруженной затяжкой. |
2. |
Вырезаем стержень DK и |
|
рассматриваем его равнове- |
|
сие. Из ур-ий ∑MD=0 и |
|
∑МК=0 опр-ем реактивные |
|
усилия YD и YK, а из ур-ия |
до |
∑Х=0 найдем зависимость между HD и HK с точностью |
|
параметра Н, к-ый пока остается неизвестным. |
|
3. Равновесие рамы сохранится, если влияние удаленного |
и H |
стержня на полурамы AC и CB заменить силами: H D, YD |
|
K, YK. Из ур-ия равновесия одной из полурам найдем неизвестный параметр Н: |
|
Составными называют рамы, состоящие из нескольких со- |
|
единенных между собой простых и (или) трехшарнирных |
|
рам (рис. 4.22,а). Для расчета составные рамы, по аналогии |
|
со статически определимыми многопролетными балками, |
|
необходимо разделять на основные и вспомогательные ра- |
|
мы, то есть составить схему взаимодействия составных ча- |
|
стей. Расчет, как и в балках, начинается со второстепенных |
|
рам. Эпюры усилий для составных рам получим путем объ- |
|
единения соответствующих эпюр для отдельных рам. |
|
Например, расчет составной рамы можно выполнять в сле- |
|
дующей последовательности: 1. Сеч. I—I отрезаем правую |
|
часть рамы SE. Эта часть рамы п. с. простую раму. Опре- |
|
деляем в ней вертикальную реакцию RE в шарнирно по- |
|
движной опоре E и реактивные силы XS, YS в шарнире S. |
|
Силы взаимодействия в шарнире S учитываем при расчете |
|
последующих рам. |
|
2. Выделяем раму DKT. Она явл-ся трехшарнирной с опо- |
|
рами в разных уровнях. Опр-ив опорные реакции, постро- |
|
им |
|
эпюры усилий в ней и перейдем к расчету фрагмента ACB |
|
учитывая, кроме действующих на него нагрузок, силы вза- |
|
имодействия в шарнире D . |
|
3. Рама АСВ является трехшарнирной рамой с опо- |
|
рами в одном уровне (А и В). Особенности расчета таких рам рассмотрены ранее. Рас- |
|
смотрим расчет составной рамы, |
представленной на. Анализ ее |
структуры показывает, что ос- |
новной (главной) частью явля- |
ется ломаный стержень ADB, на |
который опирается трехшар- |
нирная рама ACB, а на после д- |
нюю - простая рама CE. Расчет |
начнем со вспомогательной рамы |
СЕ. Определим опорную реак- |
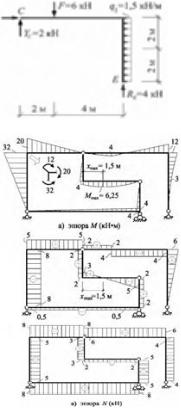
цию RE и реактивные силы в шарнире С: ΣХправ=0, Хс=1,5*4=6 кН; ΣМс прав=0,
1,5*4*2+6*2-Rk*6=0, Rk=4кН; ΣYc прав=0, -6+4+Yc=0, Yc=2кН.
Рассматривая равновесие трехшарнирной рамы AC, найдем реакции в опорах А и В . Из ур-ий:
ΣМс пр=0, -Yв*4+Хв*2+2*4*2=0, ΣМАверх=0, 12+2*4-6*4-Хв*2-Yв*8+2*4*6=0
Хв=2 кН, Yв=5кН
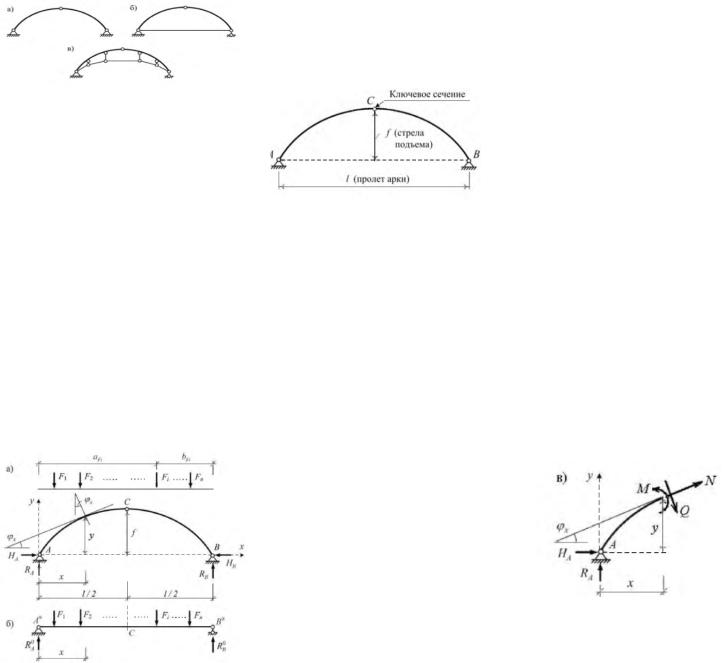
17 Образование трёхшарнирных арок, определение реакций и усилий.
Трехшарнирной называют систему, которая состоит из двух дисков, соединенных между собой шарниром, и опирающихся на землю (основание) с помощью шарнирно неподвижных опор. Трехшарнирные системы, у которых диски представлены криволинейными стержнями, называют трехшарнирными арками. основные элементы арки (рис. 4.4). Опорные сечения называют пятами. Расстояние между опорами называется пролетом. Сечение арки в точке С, в котором полуарки соединяются шарниром, называется ключевым. Высоту ключевого сечения над линией опор называют стрелой подъема арки. В зависимости от отношения стрелы подъема к пролету f / 1 различают пологие арки (при малых значениях f/1) и крутые (при больших значениях f/1). В пологих арках имеют место большие распоры и большие продольные силы. Очертание оси арки может быть задано произвольной кривой. Чаще всего арки выполняют круговыми, параболическими, синусоидальными
и т. п Вертикальные составляющие опорных реакций арки опре-
делим из ур-ий равновесия, составленных в виде сумм моментов всех сил относительно опорных точек А и В:
ΣМА=0, -Rв*l+ ΣFi aFi =0,
Rв= (ΣFi aFi )/l;
ΣМв=0, RА*l- ΣFi bFi =0, RА=
Опр-ие горизонтальных состав-
HA и HB.
ΣMc лев=0; RA l/2- ΣFi(l/2–aFi)-
HA= RA*l/2-ΣFi(l/2– aFi)/f
ΣMc пр=0; -Rв l/2+ ΣFi(l/2–bFi)-Hвf=0, Hв=Rв*l/2-ΣFi(l/2– bFi)/f, (i=1, s)
Изгибающий момент в сечении х равен алгебраической сумме моментов всех внешних сил, действующих слева от рассматриваемого сечения, относительно центра тяжести дан-
ного сечения: Mx=Mx лев=RA*Х-ΣFi(x-aFi)-Hay, (i=1, k)
Поперечная сила в сечении арки равна алгебраической сумме проекций всех внешних сил, включая опорные реакции, действующие по одну сторону от сечения, на нормаль к оси арки в этом сечении. Для сечения x получим Qx= RAcosφxF1cosφx- F2cosφx- Hsinφx= (RA-F1-F2)cosφx- Hsinφx
Продольная сила в сечении арки равна алгебраической сумме проекций всех внешних сил, включая опорные реакции, действующие по одну сторону от сечения, на касательную к оси арки в рассматриваемом сечении. Для произвольного сечения x получим:
Nx= -RAsinφx+F1sinφx+ F2sinφx- Hcosφx= -(RA-F1-F2)sinφx- Hcosφx
18.Сопоставление трёхшарнирной (распорной) системы с балкой
