
- •Минимальный набор необходимых вопросов по механике , молекулярной физике и термодинамике (для заочников)
- •Перемещение, скорость, путь, ускорение. Вычисление пройденного пути при равномерном и равноускоренном прямолинейном движении.
- •Криволинейное движение. Нормальное и тангенциальное ускорения. Кривизна траектории.
- •Угловая скорость и угловое ускорение. Вычисление угла поворота тела при равномерном и равноускоренном вращении. Связь линейных и угловых характеристик
- •Закон сохранения импульса.
- •Работа и мощность. Консервативные и неконсервативные силы.
- •Кинетическая энергия.
- •Потенциальная энергия. Связь между потенциальной энергией и силой.
- •Закон сохранения механической энергии
- •Закон всемирного тяготения. Космические скорости.
- •Момент силы и момент импульса, их запись в векторном виде.
- •Закон сохранения момента импульса.
- •Момент инерции материальной точки и твердого тела. Кинетическая энергия вращающегося тела.
- •Основной закон динамики вращательного движения.
- •Момент инерции однородных, диска, стержня, шара. Теорема Штейнера
- •Гармонические колебания. Уравнение свободных колебаний и его решение. Скорость и ускорение колеблющейся точки. Энергия гармонического колебания.
- •Математический, пружинный и физический маятники. Приведенная длина физического маятника. Центр качаний.
- •Вынужденные колебания. Резонанс. Резонансные кривые.
- •Распространение волн в упругой среде. Уравнение плоской волны. Фазовая скорость волны. Групповая скорость
- •Стоячие волны.
- •Первое начало термодинамики. Внутренняя энергия, теплота.
- •Работа газа при расширении.
- •Внутренняя энергия идеального газа
- •Уравнение состояния идеального газа. Изопроцессы. Адиабатический процесс.
- •Реальные газы. Уравнение Ван-дер-Ваальса.
- •Основное уравнение молекулярно-кинетической теории.
- •Средняя энергия молекул. Число степеней свободы газовых молекул и теплоемкость газов. Закон равнораспределения энергии по степеням свободы.
- •Скорости газовых молекул. Наиболее вероятная, средняя арифметическая и среднеквадратичная скорости газовых молекул.
- •Барометрическая формула. Распределение Больцмана
- •Средняя длина свободного пробега газовых молекул.
- •Второе начало термодинамики. Тепловые машины. Цикл Карно. Кпд цикла Карно.
- •Энтропия. Статистический смысл энтропии и 2-го начала термодинамики.
Внутренняя энергия идеального газа
![]() .
.
-
Уравнение состояния идеального газа. Изопроцессы. Адиабатический процесс.
Газ, потенциальной энергией взаимодействия между молекулами которого можно пренебречь, называется идеальным.
Уравнение Менделеева — Клапейрона (уравнение состояния идеального газа)
![]() ,
,
где т — масса газа, — молярная масса газа, R — универсальная газовая постоянная, v — количество вещества, Т — термодинамическая температура.
Опытные газовые законы, являющиеся частными случаями уравнения Менделеева — Клапейрона для изопроцессов:
а) закон Бойля—Мариотта (изотермический процесс: T=const, m=const)
![]() или
для двух состояний газа
или
для двух состояний газа
![]() ,
,
б) закон Гей-Люссака (изобарический процесс: р=const, m=const)
![]() или
для двух состояний
или
для двух состояний
![]() ,
,
в) закон Шарля (изохорический процесс: V=const, m=const)
![]() или
для двух состояний
или
для двух состояний![]() ,
,
где p1, V1, T1—давление, объем и температура газа в начальном состоянии; p2, V2, T2 — те же величины в конечном состоянии.
Адиабатический процесс - это процесс, происходящий без теплообмена с внешней средой.
Уравнение адиабаты (уравнение Пуассона) имеет вид
![]() ,
где =Cp/CV
-
показатель адиабаты.
,
где =Cp/CV
-
показатель адиабаты.
-
Реальные газы. Уравнение Ван-дер-Ваальса.
Газ, потенциальной энергией взаимодействия между молекулами которого нельзя пренебречь, называется реальным.
Уравнение Ван дер Ваальса (уравнение состояния реального газа) для одного моля реального газа
![]() .
.
-
Основное уравнение молекулярно-кинетической теории.
Основное уравнение молекулярно-кинетической теории связывает параметры состояния газа с характеристиками движения его молекул, т. е. устанавливает зависимость между давлением и объемом газа и кинетической энергией поступательного движения его молекул.
Основное уравнение кинетической теории газов,
![]()
где п — средняя кинетическая энергия поступательного движения молекулы.
-
Средняя энергия молекул. Число степеней свободы газовых молекул и теплоемкость газов. Закон равнораспределения энергии по степеням свободы.
Степенями свободы характеризуется способность системы (в нашем случае молекулы) совершать независимые движения. В соответствии с видами механического движения различают поступательные, вращательные и колебательные степени свободы.
Числом степеней свободы механической системы называется количество независимых величин, однозначно определяющих ее положение и конфигурацию в пространстве.
Закон равнораспределения по степеням свободы: если система молекул находится в состоянии теплового равновесия при температуре T, то средняя кинетическая энергия равномерно распределена между всеми поступательными и вращательными степенями свободы и для каждой поступательной или вращательной степени она равна kT/2 , а энергия, приходящаяся на колебательную степень свободы, равна kT (где k — постоянная Больцмана).
Средняя
полная кинетическая энергия молекулы
с жесткими связями, включающая кинетическую
энергию поступательного и вращательного
движения, вычисляется по формуле
![]() .
.
-
Скорости газовых молекул. Наиболее вероятная, средняя арифметическая и среднеквадратичная скорости газовых молекул.
В газе, находящемся в состоянии равновесия, устанавливается некоторое стационарное, не меняющееся со временем распределение молекул по скоростям (v), которое подчиняется закону, теоретически полученному Максвеллом. Закон Максвелла представлен в виде некоторой функцией f(v), называемой функцией распределения молекул по скоростям. Если разбить диапазон скоростей молекул на малые интервалы, равные dv, то на каждый интервал скорости будет приходиться некоторое число молекул dN(v), имеющих скорость, заключенную в этом интервале. Функция f(v) представляет собой отношение доли (относительного количества) молекул dN(v)/N, скорости которых лежат в интервале от v до v + dv, в величине этого интервала dv.
![]() (1)
(1)
Применяя методы теории вероятности, Максвелл нашел функцию f(v), т.е. закон для распределения молекул идеального газа по скоростям:
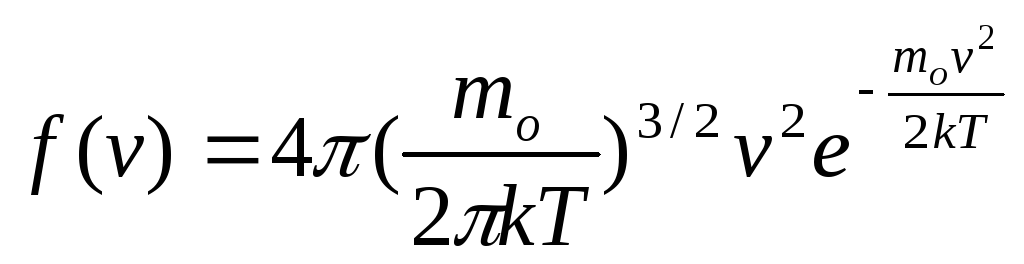 (2)
(2)
Здесь mo – масса одной молекулы.
Вид функции этой функции
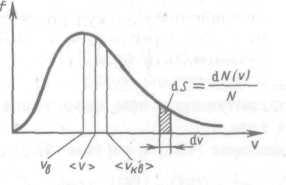
Используя ее можно получить выражения для следующих скоростей молекул:
![]() —
средняя
квадратичная;
—
средняя
квадратичная;
![]() —
средняя
арифметическая;
—
средняя
арифметическая;
![]() —
наиболее
вероятная,
—
наиболее
вероятная,
где то — масса одной молекулы.
