2.3 Отработка результатов косвенных измерений

2.3.1 Метод частных производных

Пусть интересующая нас величина y является некоторой функцией других величин x_l, x₂, x₃ и т.д., так что

у = ƒ(x_l, x₂, x₃...) (11)

причем величины x_l, x₂, x₃... мы можем измерять путем прямых измерений. В этом случае мы для определения величин и ∆ сначала измеряем все величины, от которых зависит у (x_l, x₂, x₃...) по методике, изложенной в предыдущем параграфе. В результате чего определяем , а также полные погрешности, в определении этих величин, которые обозначим как Наилучшее (среднее) значение косвенно определяемой величины у находится при подстановке в (11) наилучших (средних) значений

(12)

Для определения полной абсолютной погрешности величины у необходимо выяснить, как изменяется эта величина при относительно небольших изменениях всех величин, от которых зависит величина у. Это можно сделать с помощью полного дифференциала. Интересующее нас изменение величины

(13)

где 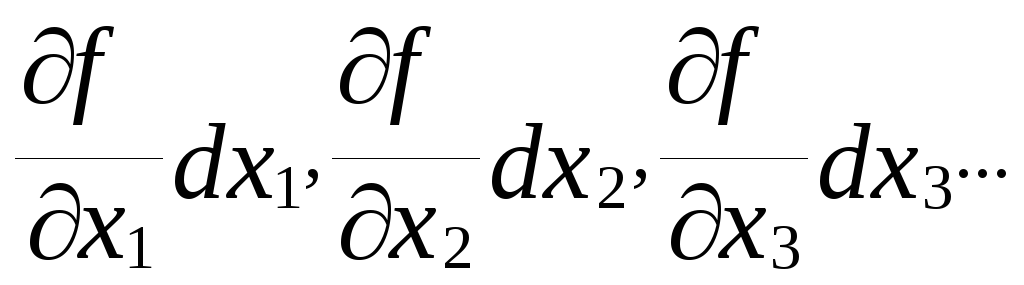– обозначают частные производные от функции f по соответствующим переменным. Эти частные производные вычисляются при наилучших (средних) значениях и т.д.

От бесконечно малых изменений величин у, x_l, x₂, x₃... в (13) перейдем к конечным значениям их изменений

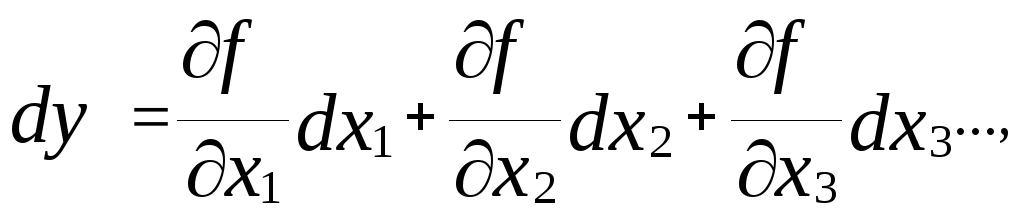(14)

где ∆y- искомая полная погрешность величины - значения соответствующих частных производных, вычисленных при наилучших (средних) значениях входящих в них величин.

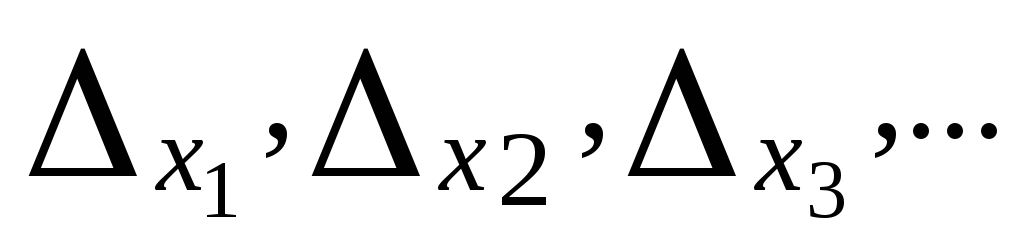- полные погрешности определения величин.

Под частной производной функции ƒ(x, y, z) по переменной X понимают величину:

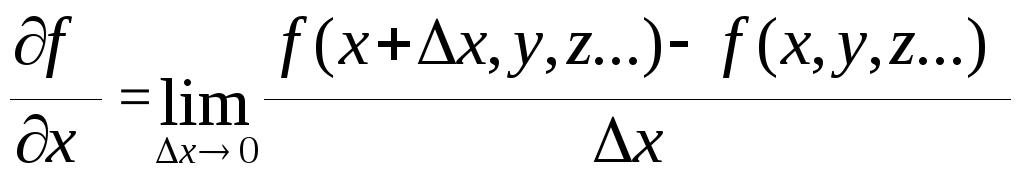(15)

т.е. это производная, которая вычисляется в предположении, что все переменные, кроме той, по которой берется производная, являются постоянными величинами. Например: пусть . Тогда

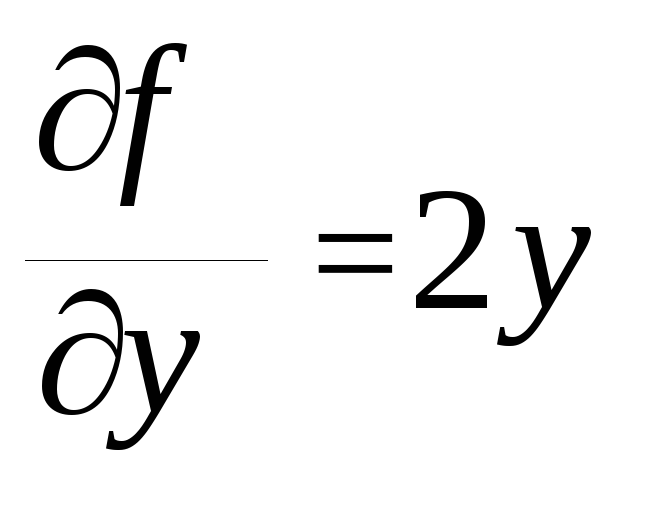
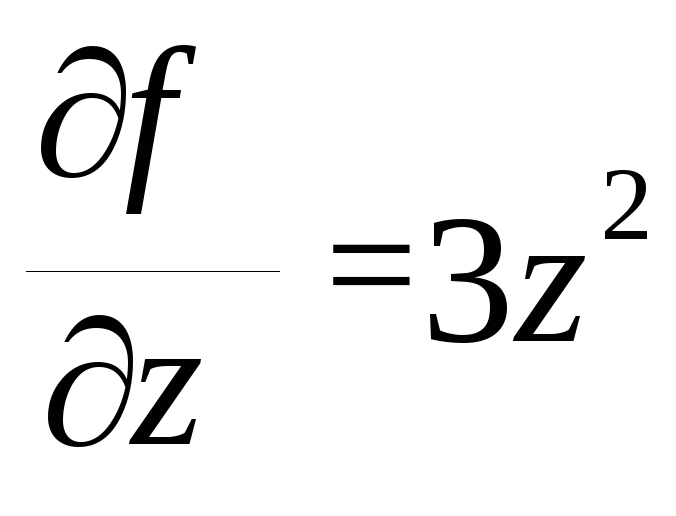
После вычисления абсолютной ошибки ∆у по формуле (12) находят относительную ошибку как

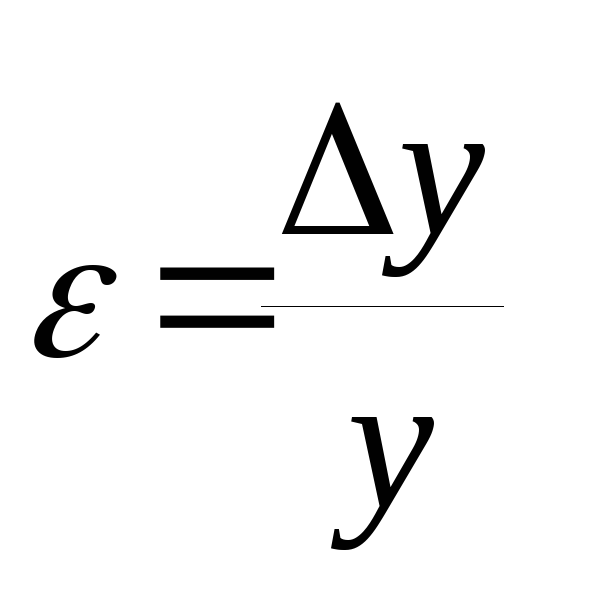(16)

Этот способ удобен в том случае, когда представляет собой алгебраическую сумму.

2.3.2 Метод логарифмирования и дифференцирования

Если в явном виде функция содержит произведения и (или) частное от деления предпочтителен другой способ. Он основан на том факте, что дифференциал от натурального логарифма дает относительную ошибку измерений:

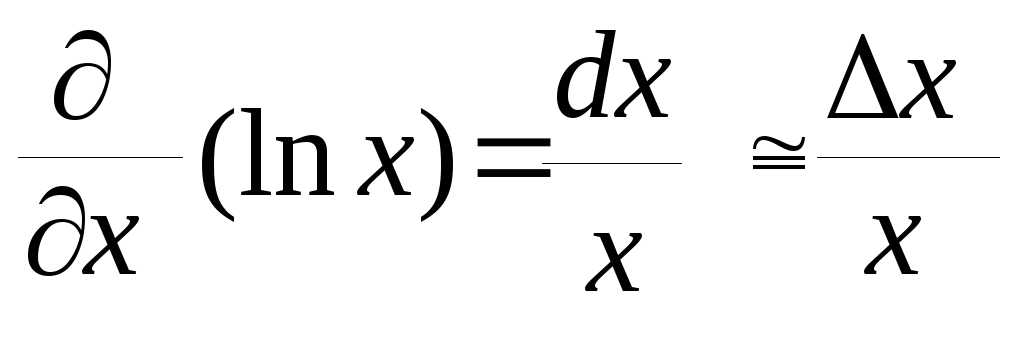(17)

3 Общая схема обработки измерений

Схему обработки измерений проиллюстрируем на конкретном примере. Предположим, что нам нужно определить ускорение тела, движущегося равноускоренно, без начальной скорости в соответствии с уравнением 18. Выразим ускорение тела из формулы пути для равноускоренного движения:

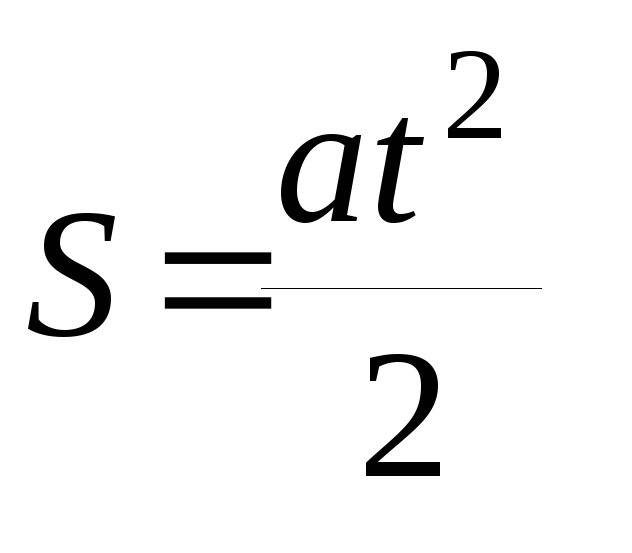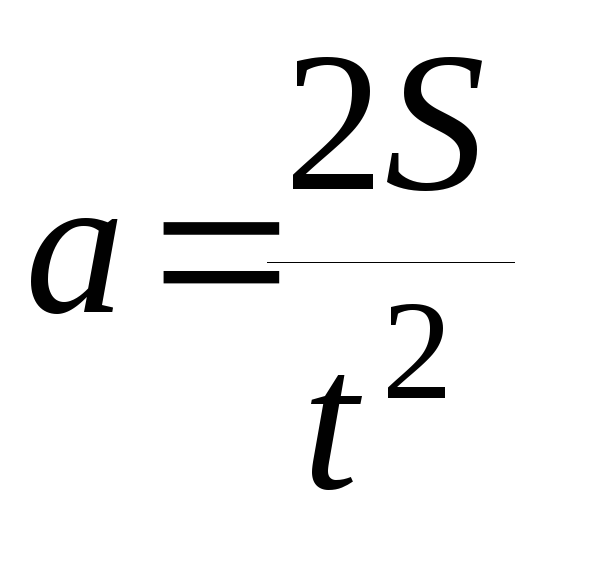; . (18)

Здесь S и t - прямо измеряемые величины, а - косвенно измеряемая величина. Обработку результатов проводим в следующей последовательности:

3.1 Проводим n опытов и получаем n значений S и t. Находим средние значения и

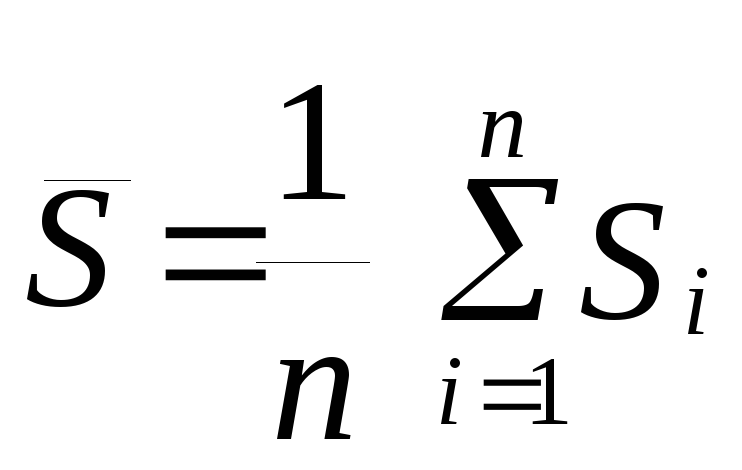; (19)

и подставив их в (18), находим среднее значение ускорения

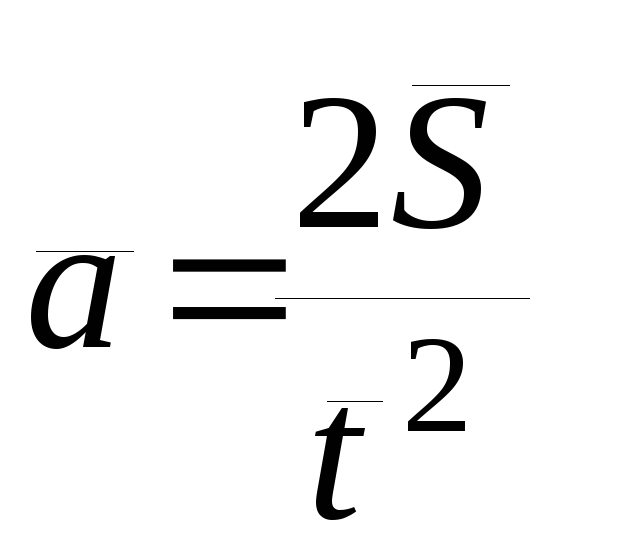(20)

3.2 Определяем полную ошибку прямо измеренных величин. Для этого:

3.2.1  Явно сомнительные результаты отбросить как промахи или повторить измерения.

3.2.2  Определить приборные ошибки икак половину цены наименьшего деления шкалы или полного наименьшего разряда цифрового прибора.

3.2.3  Рассчитать среднюю случайную ошибку икак среднее значения разностей и

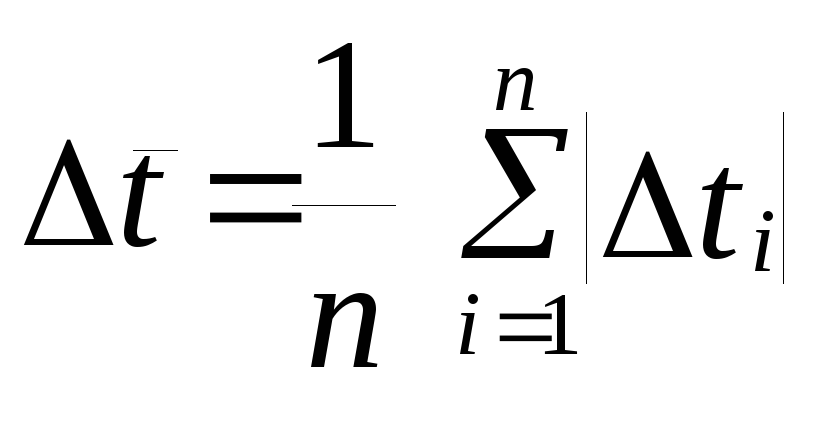; (21)

Расчет значений ипроводить до того знака после запятой, который фигурирует в соответствующих приборных ошибках и.

3.2.4 Сравнить средние случайные ошибки измерений пути и времени с их приборными ошибками. В качестве полных ошибок ∆S и ∆t взять большие значения и;и

3.3  Расчет погрешностей косвенно измеренной величины производится следующим образом:

3.3.1 Продифференцировать расчетную формулу (20) поочередно по переменным S и t:

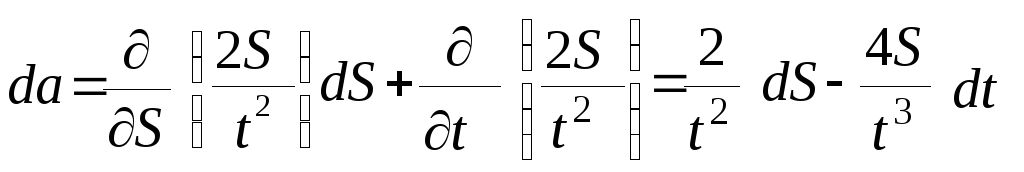(22)

3.3.2 Так как da≈∆a, ds≈∆s и dt≈∆t, равенство (22) можно записать:

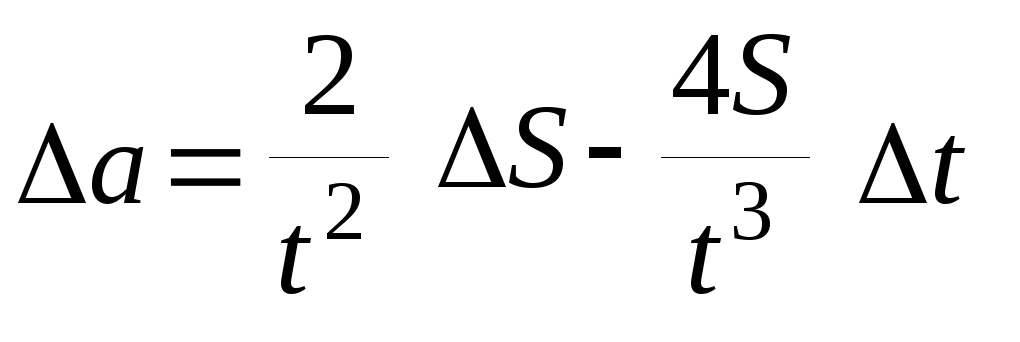(23)

3.3.3 Слагаемые со знаком минус по модулю, т.к. ошибки прямо измеренных величин складываются. Вместо ∆S и ∆t подставить их полные ошибки ∆_s и ∆_t.

Тогда формула для расчета абсолютной ошибки прямо измеренной величины а записывается:

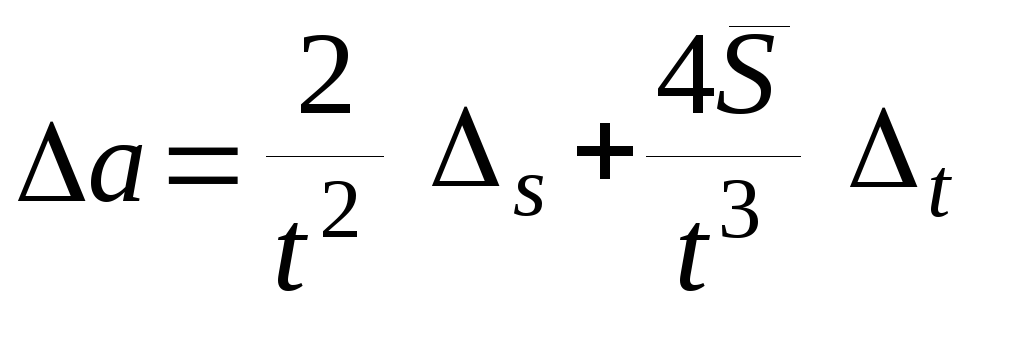, (24)

3.3.4 Рассчитать относительную ошибку измерения ускорения по формуле

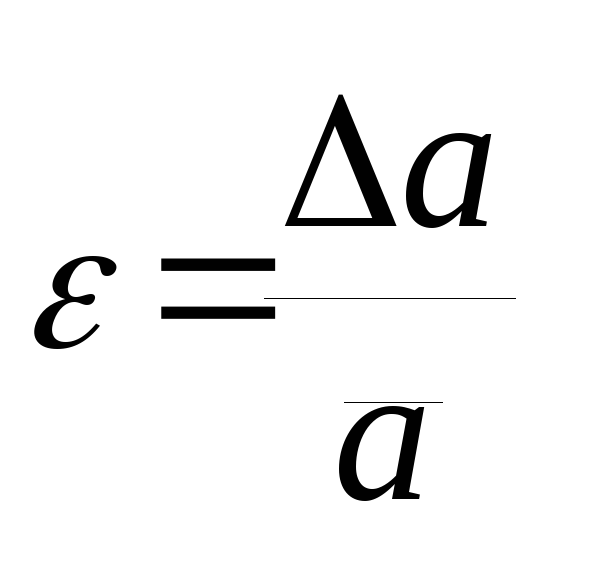(25)

Примечание. В данном случае связь между a и S и t выражается в виде частного. Поэтому в этом случае проще проводить вычисления вторым способом с предварительным логарифмированием по следующей схеме:

3.4 Прологарифмировать расчетную формулу

lna=ln2+lnS-2lnt (26)

3.5. Продифференцировать (26) по переменным S и t:

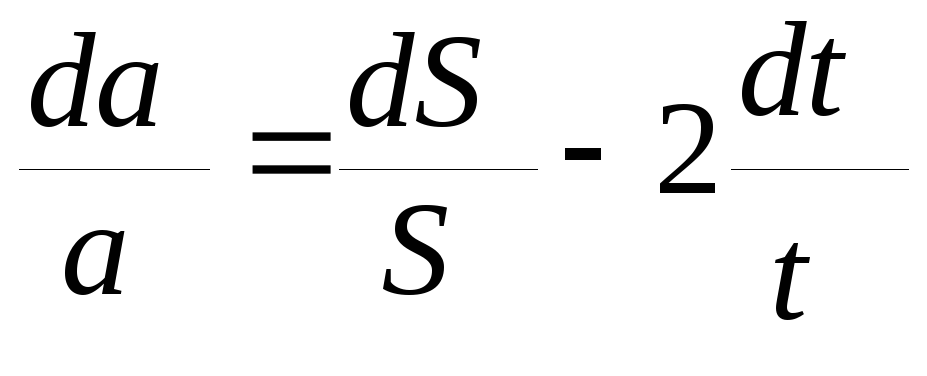(27)

3.6 Поменять знак у второго слагаемого и записать (27) в виде

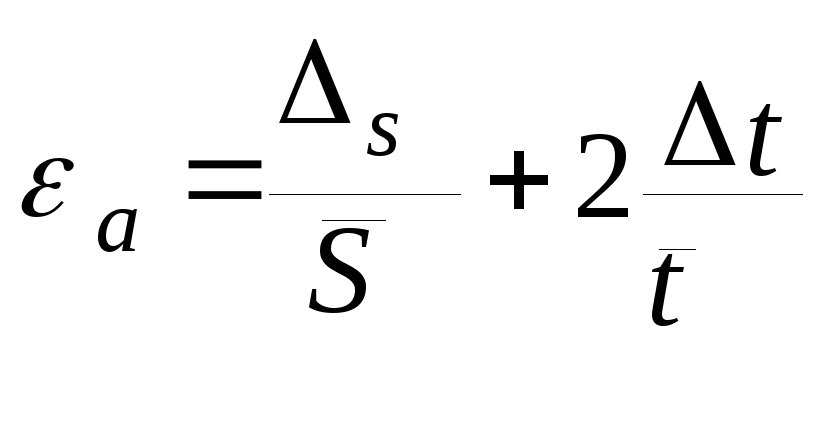(28)

3.7 Рассчитать относительную ошибку по формуле (28), а абсолютную, как

(29)

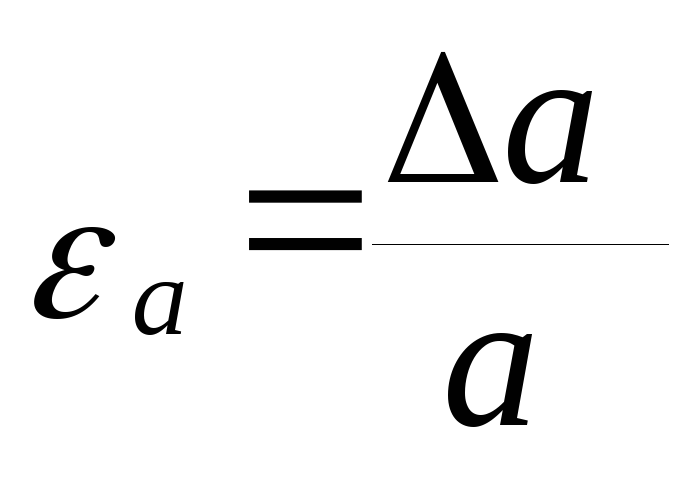
Отметим, что оба способа приводят к одинаковому результату. Например, получим формулу для расчета относительной ошибки , используя формулу (23):

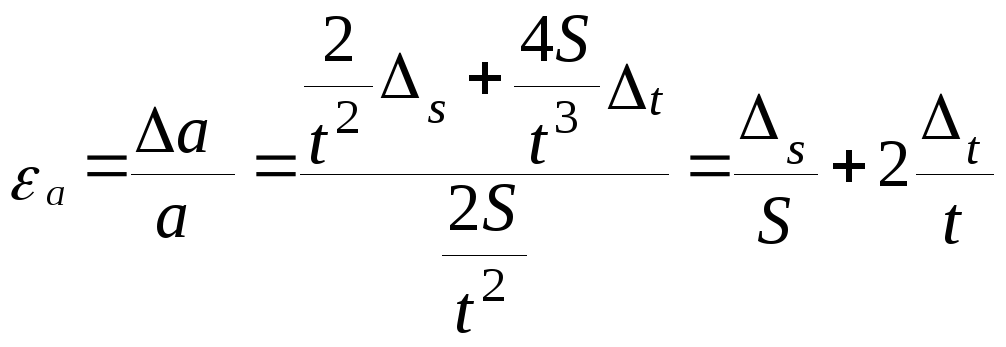(30)

Формула (30) аналогичная формуле (27), полученной вторым способом. Однако расчет вторым способом в данном случае проще.