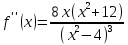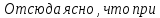- •Предел функции.
- •Правила вычисления производных, связанные с арифметическими действиями над функциями.
- •Найти , если и .
- •Производная и дифференциал функции. Уравнение касательной прямой.
- •Провести полное исследование функции и построить её график.
- •1)Свойства функций, непрерывных в точке
- •2) Методы решения задач аналитической геометрии
1)Свойства функций, непрерывных в точке
Теорема об алгебраических свойствах функций, непрерывных в точке
Если функции
f и g непрерывны в точке x0, то функции cf
(c — постоянное), f + g, f − g, f · g, а если,
кроме того, g(x0)
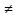 0,
то и f /g , также непрерывны в точке x0.
0,
то и f /g , также непрерывны в точке x0.
Эта теорема вытекает непосредственно из определения 1 непрерывности функции в точке и свойств пределов функции, установленных на прошлой лекции.
Докажем, например, непрерывность функции произведения f · g функций f и g. Согласно cвойств пределов функций, имеем
lim x→x0 (f · g)(x) = lim x→x0 f (x) lim x→x0 g(x) = f (x0)g(x0),
ибо пределы limx→x0 f (x) и limx→x0 g(x) существуют и равны в силу непрерывности f и g в точке x0 равны соответственно f (x0) и g(x0). Теперь выполнение доказанного выше равенства и означает непрерывность функции f · g в точке x0
Непрерывность сложной функции в точке
Теорема о непрерывности сложной функции в точке
Пусть функция y = f (x) непрерывна в точке x0, а функция z = F(y) непрерывна в точке y0 = f (x0). Тогда сложная функция или суперпозиция функций F[f (x)] непрерывна в точке x0.
Короче, но менее точно: непрерывная функция от непрерывной функции является непрерывной функцией.
Замечание.
Следует обратить внимание на то, что в теореме утверждается непрерывность сложной функции F[f (x)] в точке x0, а поскольку непрерывность функции в некоторой точке предполагает согласно определению 1 непрерывности функции в точке, что эта функция определена в некоторой окрестности точки x0.

Правило замены переменного для пределов непрерывных функций
Утверждение теоремы можно записать в виде формулы
lim x→x0 F[f (x)] = F[ lim x→x0 f (x)],
из которой видно, что операция предельного перехода перестановочна с операцией предельного перехода у непрерывной функцией.
В самом деле, левая часть предыдущего равенства равна F[f (x0)] согласно утверждению теоремы, правая часть также равна F[f (x0)] в силу непрерывности функции f (x) в точке x0.
При отыскании пределов непрерывных функций теорему о непрерывности сложной функции в точке удобно использовать в ещё в одном виде, в виде следующего правила
Правило замены переменного для пределов непрерывных функций
lim x→x0 F[f (x)] = lim y→y0 F(y), y = f (x).
Еще пару свойств функций, непрерывных в точке
Замечание.
Теорема о непрерывности сложной функции в точке переносится и на случай односторонней непрерывности.
Свойство 1. Если f : (a, b) → R и g : (a, b) → R непрерывны в точке x0 ∈ (a, b) и f (x) ≥ g(x) для всех x ∈ (a, b)\{x0}, то и в точке x0 верно это неравенство f (x0) ≥ g(x0).
Свойство 2. Если f : (a, b) → R непрерывна в точке x0 ∈ (a, b), то существует такой открытый интервал (c, d) ⊂ (a, b) , содержащий точку x0, на котором функция f будет ограниченной.
2) Методы решения задач аналитической геометрии
Аналитическая геометрия – это раздел в геометрии, в котором геометрические фигуры и их свойства исследуются средствами алгебры.
В основе решения задач данного раздела геометрии лежит метод координат. Согласно методу координат каждому геометрическому соотношению ставится в соответствие некоторое уравнение, которое связывает координаты фигуры или тела.
Основателем аналитической геометрии полноправно считается Декарт, который в 1637 году серьезно взялся за развитие данного направления в математике. Среди ученых, внесших свой вклад в развитие аналитической геометрии, можно выделить Ньютона, Лейбница и др.
Все, что изучается в аналитической геометрии, можно разделить на два основных раздела:
-
аналитическая геометрия на плоскости, изучающая такие элементы как преобразование координат, прямая, эллипс, окружность, парабола и гипербола;
-
аналитическая геометрия в пространстве, изучающая плоскость, сферу, прямую.
Аналитическая геометрия: основные формулы
При решении задач по аналитической геометрии в первую очередь используются различные действия над векторами, которые заданы в координатной форме. Приведем примеры часто используемых формул:
-
расстояние между двумя точками:

-
угол между векторами:

-
деление отрезка в отношении λ:
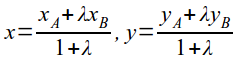
Понятие «уравнение линии» это элемент дальнейшего развития метода координат. Через любые две точки на плоскости можно провести прямую. Таким образом, если точка на плоскости определяется двумя числами (т.е. координатами точки), то линия на плоскости определяется уравнением, которое связывает координаты любой точки линии.
Приведем примеры некоторых уравнений:
-
общее уравнение прямой на плоскости:
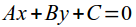
-
Уравнение окружности радиуса r с центром в точке (x0, y0):
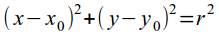
-
и многие другие.
Если же мы имеем дело с пространством, то там все аналогично плоскости, за исключением того, что координат используется не две, а три.
Приведем примеры уравнений и формул, используемых в пространственной аналитической геометрии:
-
уравнение сферы:
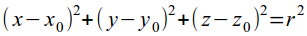
-
расстояние между двумя точками:
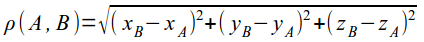
-
и т.д.
Аналитическая геометрия: этапы решения задач
Не знаете, с какого края подступиться к решению задачи? Предлагаем вашему вниманию некоторый алгоритм решения любой задачи по аналитической геометрии. Вам останется всего на всего запомнить четыре этапа, из которых состоит решение задачи, и решение любой задачи окажется вам «по плечу».
Этап 1. Определение вида задачи. На данном этапе нужно всего лишь определить «плоская» или пространственная задача предложена для решения.
Этап 2. Определить какие геометрические фигуры используются в условии задачи.
Этап 3. Выполнение чертежа. Чертеж лучше делать всегда, даже если этого не требуется по условию. Поверьте, это очень помогает при решении задачи.
Этап 4. Составление алгоритма решения и его выполнение. Как правило, задачи в геометрии не решаются в одну строчку. Поэтому для большей наглядности и упрощения себе жизни само решение и его оформление лучше разбить на сгруппированные по смыслу пункты.
Руководствуясь этими простыми этапами и помня основные формулы, можно решить любую, пусть даже самую сложную, задачу.
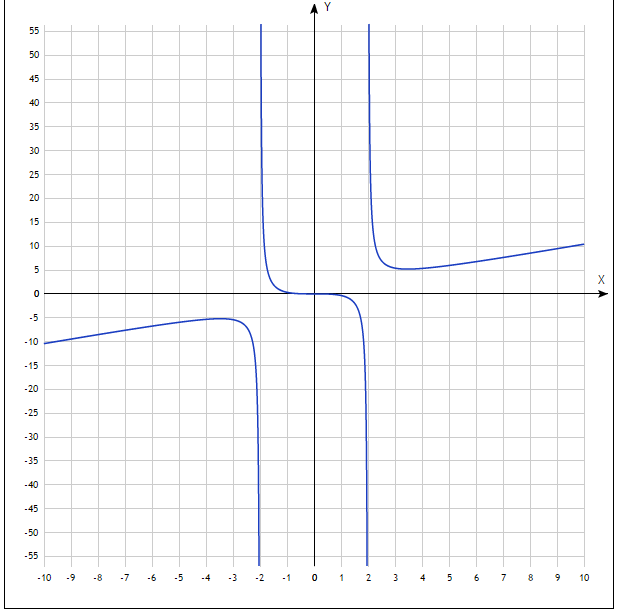
3.Провести
полное исследование функции
 и построить её график.
и построить её график.
1)
Область
определения:
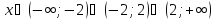
2) Непериодическая. Проверим на четность-нечетность:
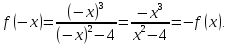 Значит,
функция нечетная.
Значит,
функция нечетная.
3) Найдем точки пересечения с осями координат.
График
пересекает ось Y
в том случае, когда x=0
=>
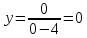 ,
т.е. график пересекает ось Y
в точке (0;0).
,
т.е. график пересекает ось Y
в точке (0;0).
График
пересекает ось X
в том случае, когда y=0
=>
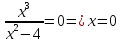 ,
т.е. график пересекает ось X
в точке (0;0)
,
т.е. график пересекает ось X
в точке (0;0)
-
Найдем интервалы знакопостоянства:
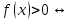
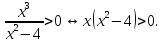 Тогда
получаем следующее (решив методом
интервалов):
Тогда
получаем следующее (решив методом
интервалов):
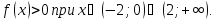
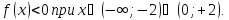
-
Найдем асимптоты.
Вертикальные асимптоты:
 ,
значит x=2
– вертикальная асимптота. В силу
симметрии (нечетная функция) x=
- 2 также является вертикальной асимптотой.
,
значит x=2
– вертикальная асимптота. В силу
симметрии (нечетная функция) x=
- 2 также является вертикальной асимптотой.
Наклонные асимптоты:

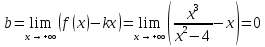
Значит, прямая y=x – наклонная асимптота.
-
Найдем интервалы монотонности и экстремумы функции, исследуя первую производную:
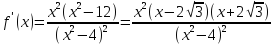

Отсюда
видно, что при x0
функция имеет минимум в точке x=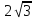 ,
убывает на (0;2) и (2;
,
убывает на (0;2) и (2;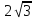 )
и возрастает на (
)
и возрастает на (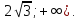 Аналогично, для x<0
(функция нечетна, а значит симметрична
относительно начала координат).
Аналогично, для x<0
(функция нечетна, а значит симметрична
относительно начала координат).
-
Чтобы определить интервалы выпуклости и точки перегиба, вычислим вторую производную: