
Министерство образования и науки РФ
.pdf
Коэффициент готовности, равный вероятности безотказной работы, для систем с
облегченным режимом равен
|
|
|
s |
k |
|
|
kгот 1 Ps |
1 [ (s 1) 0 |
] / 1 (s 1) 0 |
|
(20) |
||
|
|
|
k 1 |
i 1 |
|
|
Для систем с холодным резервированием 0 0 и. стало быть 0 0 , получаем
kгот (1 s ) |
(1 s 1 ) |
|
(21) |
|||
Для систем с горячим резервированием |
0 |
получаем |
||||
|
|
|
s |
|
|
|
|
|
(s i 1)r |
|
|
||
kгот 1 |
|
i 1 |
|
|
(22) |
|
|
s |
k |
|
|||
|
(s i 1)r |
|
|
|||
|
k 1 |
i 1 |
|
|
||
Формулы (21) и (22) являются расчетными для анализа установившихся режимов в системах с восстановлением.
2. Анализ надежности системы с горячим и холодным резервированием методом имитационного моделирования во многом аналогичен методам, рассмотренным в предыдущей работе. Разница состоит в том, что в нашем случае транзакт, выйдя из канала обслуживания (из многоканального устройства), не покидает систему, а направляется в ремонт. Если прибор, имитирующий механика по ремонту, занят, транзакт становится в очередь. Задержавшись в этом приборе на время ремонта, транзакт блоком TRANSFER вновь возвращается в работу. Второй сегмент GPSS – программы полностью идентичен такому же в ранее рассмотренной программе. Различие состоит только в том, что для получения результатов моделирования необходимо проверку состояния прибора (многоканального устройства) производить через весьма большой интервал времени, когда режим работы системы можно считать установившимся.
Пример выполнения практической работы №4
1. Дана вычислительная система с горячим резервированием. Резервирование двукратное: 1 ЭВМ - рабочая, две – резервные (s=3). Среднее время наработки одной ЭВМ на отказ – 20 часов (интенсивность отказов λ = 1/t = 0.05 1/час). Интенсивность восстановления μ равно 0.1 1/час.
Определить вероятность того, что система является работоспособной (в начале работы все ЭВМ исправны). Решение получить в установившемся режиме (расчет с помощью аналитического решения и методом имитационного моделирования) и в переходном режиме, решая численным методом систему дифференциальных уравнений.
1.1 Решение задачи в среде MathCAD
Коэффициент готовности системы с горячим резервированием и с восстановлением вышедших из строя элементов вычисляем по формулам (22). Ниже приведен фрагмент MATHCAD – программы:
21

r |
l |
s |
|
||
m |
|
||||
|
|
|
|
(s i 1) r |
|
|
|
k 1 |
|
i 1 |
|
|
|
|
|
|
|
|
|
|
s |
k |
|
|
|
|
|
||
|
|
|
1 |
(s i 1) r |
|
|
|
|
|
k 1 |
i 1 |
k 

Таким образом, вероятность безотказной работы системы (коэффициент готовности) в установившемся режиме равна 0,842.
Решение системы уравнений Колмогорова (15) методом Рунге – Кутты дается в следующем фрагменте:
22
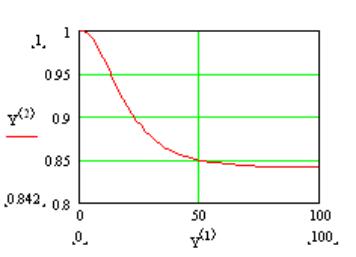
Рис. 9. Вероятность исправной работы системы с горячим резервированием (и с восстановлением вышедших из строя элементов) как функция времени.
Результаты этих решений полностью совпадают .
1.2 Решение задачи методом имитационного моделирования. Ниже приведены текст GPSS – программы и результаты ее работы.
RMULT |
223 |
|
EXPON1 |
FUNCTION RN1,C24 |
EXPONENTIAL DISTRIBUTION |
0,0/.100,.104/.200,.222/.300,.355/.400,.509/.500,.690/.600,.915/.700,1.200/.7
50,1.380/.800,1.600/
.840,1.830/.880,2.120/.900,2.300/.920,2.520/.940,2.810/.950,2.990/.960,3.200/
.970,3.500/.980,3.900/
.990,4.600/.995,5.300/.998,6.200/.999,7/1,8
|
COMP |
STORAGE |
3 |
|
GENERATE |
,,,3 |
|
L1 |
ENTER |
COMP |
|
|
ADVANCE |
20,FN$EXPON1 |
|
|
LEAVE |
COMP |
|
|
QUEUE |
LINE |
|
|
SEIZE |
remont |
|
|
DEPART |
LINE |
|
|
ADVANCE |
10,FN$EXPON1 |
|
|
RELEASE |
remont |
|
|
TRANSFER |
,L1 |
|
|
GENERATE |
100 |
|
|
TEST E SE$COMP,0,L2 |
|
|
|
SEIZE |
NUMBER |
|
|
RELEASE |
NUMBER |
|
L2 |
TERMINATE |
1 |
|
|
START |
1000 |
|
23
|
START TIME |
|
END TIME |
BLOCKS |
FACILITIES |
|
STORAGES |
|
|
|
|||||
|
|
0.000 |
|
100000.000 |
|
15 |
|
2 |
|
1 |
|
|
|
||
|
NAME |
|
|
|
|
VALUE |
|
|
|
|
|
|
|
||
|
COMP |
|
|
|
|
10007.000 |
|
|
|
|
|
|
|
||
|
EXPON1 |
|
|
|
|
10006.000 |
|
|
|
|
|
|
|
||
|
L1 |
|
|
|
|
|
2.000 |
|
|
|
|
|
|
|
|
|
L2 |
|
|
|
|
|
15.000 |
|
|
|
|
|
|
|
|
|
LINE |
|
|
|
|
10008.000 |
|
|
|
|
|
|
|
||
|
NUMBER |
|
|
|
|
10010.000 |
|
|
|
|
|
|
|
||
|
REMONT |
|
|
|
|
10009.000 |
|
|
|
|
|
|
|
||
LABEL |
|
LOC |
BLOCK TYPE |
|
ENTRY COUNT CURRENT |
COUNT RETRY |
|
|
|||||||
|
|
1 |
GENERATE |
|
|
|
3 |
|
|
0 |
0 |
|
|
|
|
L1 |
|
2 |
ENTER |
|
|
|
7852 |
|
|
0 |
0 |
|
|
|
|
|
|
3 |
ADVANCE |
|
|
7852 |
|
|
2 |
0 |
|
|
|
||
|
|
4 |
LEAVE |
|
|
|
7850 |
|
|
0 |
0 |
|
|
|
|
|
|
5 |
QUEUE |
|
|
|
7850 |
|
|
0 |
0 |
|
|
|
|
|
|
6 |
SEIZE |
|
|
|
7850 |
|
|
0 |
0 |
|
|
|
|
|
|
7 |
DEPART |
|
|
7850 |
|
|
0 |
0 |
|
|
|
||
|
|
8 |
ADVANCE |
|
|
7850 |
|
|
1 |
0 |
|
|
|
||
|
|
9 |
RELEASE |
|
|
7849 |
|
|
0 |
0 |
|
|
|
||
|
|
10 |
TRANSFER |
|
|
7849 |
|
|
0 |
0 |
|
|
|
||
|
|
11 |
GENERATE |
|
|
1000 |
|
|
0 |
0 |
|
|
|
||
|
|
12 |
TEST |
|
|
|
1000 |
|
|
0 |
0 |
|
|
|
|
|
|
13 |
SEIZE |
|
|
|
|
846 |
|
|
0 |
0 |
|
|
|
|
|
14 |
RELEASE |
|
|
|
846 |
|
|
0 |
0 |
|
|
|
|
L2 |
|
15 |
TERMINATE |
|
|
1000 |
|
|
0 |
0 |
|
|
|
||
FACILITY |
|
ENTRIES |
UTIL. |
AVE. TIME AVAIL. OWNER PEND |
INTER RETRY |
|
|||||||||
DELAY |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
REMONT |
|
7850 |
0.788 |
|
10.043 |
1 |
|
4 |
0 |
0 |
|
0 |
|
||
NUMBER |
|
846 |
0.000 |
|
0.000 |
1 |
|
0 |
0 |
0 |
|
0 |
|
||
QUEUE |
|
MAX CONT. ENTRY ENTRY(0) AVE.CONT. AVE.TIME |
AVE.(-0) |
|
|||||||||||
RETRY |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
LINE |
|
2 |
0 |
7850 |
|
3109 |
0.636 |
8.104 |
13.419 |
0 |
|||||
STORAGE |
|
CAP. REM. MIN. MAX. |
ENTRIES AVL. |
AVE.C. UTIL. RETRY |
|
||||||||||
DELAY |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
COMP |
|
3 |
1 |
0 |
|
3 |
7852 |
1 |
1.575 |
0.525 |
0 |
|
0 |
||
FEC XN |
PRI |
BDT |
|
ASSEM |
CURRENT |
NEXT |
PARAMETER |
VALUE |
|
|
|
||||
4 |
0 |
100006.349 |
4 |
|
|
8 |
9 |
|
|
|
|
|
|
|
|
1 |
0 |
100040.889 |
1 |
|
|
3 |
4 |
|
|
|
|
|
|
|
|
1004 |
0 |
100100.000 |
1004 |
|
|
0 |
11 |
|
|
|
|
|
|
|
|
3 |
0 |
100109.907 |
3 |
|
|
3 |
4 |
|
|
|
|
|
|
|
|
Из 1000 проверок (транзакты, прошедшие через блок TEST) 846 закончились успешно. Вероятность исправной работы - 0.846. Расхождение результатов с аналитическим решением равно 0.4 процента! Очень высокая точность, которую можно еще повысить, увеличивая время моделирования.
1.2Дана та же самая система, что и в пункте 1.1, только резервирование – холодное.
2.1Решение задачи в среде MathCAD
24
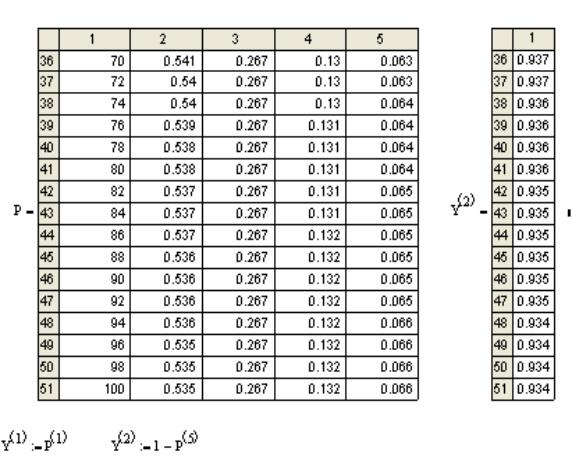
Фрагмент MATHCAD – программы:
|
l 0.05 |
|
|
s 3 |
|
|
|
r |
l |
|
m 0.1 |
|
||
|
|
|
|
|
m |
|
|
|
||||||
|
|
|
|
|
|
1 rs |
|
|
|
|
|
|||
|
|
|
khol |
|
|
|
|
|
|
|
||||
|
|
|
1 rs 1 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
khol 0.933 |
|
|
m 0.1 |
l 0.05 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l P |
m P |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
1 |
|
|
|
l P |
l P m P m P |
||||||
|
|
|
|
|
|
|
||||||||
|
|
|
|
f(t P) |
|
2 |
1 |
3 |
2 |
|
||||
|
|
|
0 |
l P |
l P m P m P |
|||||||||
|
P |
|
|
|
||||||||||
|
|
0 |
|
|
|
|
3 |
2 |
4 |
3 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
m P4 l P3 |
|
||||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
0 |
|
|
|
|
|
|
|||||
P:=rkfixed(P,0,100,50,f)
25
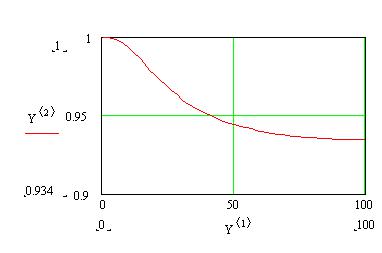
Рис. 10. Вероятность исправной работы системы с холодным резервированием (и с восстановлением вышедших из строя элементов) как функция времени.
2.2 Решение задачи методом имитационного моделирования. (текст GPSS – программы и результаты ее работы)
RMULT |
223 |
|
EXPON1 |
FUNCTION RN1,C24 |
EXPONENTIAL DISTRIBUTION |
0,0/.100,.104/.200,.222/.300,.355/.400,.509/.500,.690/.600,.915/.700,1.200/.7
50,1.380/.800,1.600/
.840,1.830/.880,2.120/.900,2.300/.920,2.520/.940,2.810/.950,2.990/.960,3.200/
.970,3.500/.980,3.900/
.990,4.600/.995,5.300/.998,6.200/.999,7/1,8
|
GENERATE |
,,,3 |
L1 |
SEIZE |
COMP |
|
ADVANCE |
20,FN$EXPON1 |
|
RELEASE |
COMP |
|
QUEUE |
LINE |
|
SEIZE |
remont |
|
DEPART |
LINE |
|
ADVANCE |
10,FN$EXPON1 |
|
RELEASE |
remont |
|
TRANSFER |
,L1 |
|
GENERATE |
100 |
|
TEST E F$COMP,1,L2 |
|
|
SEIZE |
NUMBER |
|
RELEASE |
NUMBER |
L2 |
TERMINATE |
1 |
|
START |
1000 |
START TIME |
END TIME BLOCKS FACILITIES |
STORAGES |
|
|
0.000 |
100000.000 |
15 |
3 |
0 |
NAME |
|
VALUE |
|
|
COMP |
10007.000 |
|
|
|
EXPON1 |
10006.000 |
|
|
|
L1 |
|
2.000 |
|
|
L2 |
|
15.000 |
|
|
26
|
LINE |
|
|
|
|
10008.000 |
|
|
|
|
|
|
|
NUMBER |
|
|
|
|
10010.000 |
|
|
|
|
|
|
|
REMONT |
|
|
|
|
10009.000 |
|
|
|
|
|
|
LABEL |
|
LOC |
BLOCK TYPE |
ENTRY COUNT CURRENT |
COUNT RETRY |
|
|
|||||
|
|
1 |
GENERATE |
|
|
3 |
|
0 |
0 |
|
|
|
L1 |
|
2 |
SEIZE |
|
|
4590 |
|
0 |
0 |
|
|
|
|
|
3 |
ADVANCE |
|
4590 |
|
1 |
0 |
|
|
||
|
|
4 |
RELEASE |
|
4589 |
|
0 |
0 |
|
|
||
|
|
5 |
QUEUE |
|
|
4589 |
|
1 |
0 |
|
|
|
|
|
6 |
SEIZE |
|
|
4588 |
|
0 |
0 |
|
|
|
|
|
7 |
DEPART |
|
4588 |
|
0 |
0 |
|
|
||
|
|
8 |
ADVANCE |
|
4588 |
|
1 |
0 |
|
|
||
|
|
9 |
RELEASE |
|
4587 |
|
0 |
0 |
|
|
||
|
|
10 |
TRANSFER |
|
4587 |
|
0 |
0 |
|
|
||
|
|
11 |
GENERATE |
|
1000 |
|
0 |
0 |
|
|
||
|
|
12 |
TEST |
|
|
1000 |
|
0 |
0 |
|
|
|
|
|
13 |
SEIZE |
|
|
|
931 |
|
0 |
0 |
|
|
|
|
14 |
RELEASE |
|
|
931 |
|
0 |
0 |
|
|
|
L2 |
|
15 |
TERMINATE |
|
1000 |
|
0 |
0 |
|
|
||
FACILITY |
|
ENTRIES |
UTIL. |
AVE. TIME AVAIL. OWNER PEND INTER RETRY |
|
|||||||
DELAY |
|
|
|
|
|
|
|
|
|
|
|
|
COMP |
|
4590 |
0.938 |
|
20.427 |
1 |
4 |
0 |
0 |
0 |
|
|
REMONT |
|
4588 |
0.461 |
|
10.041 |
1 |
1 |
0 |
0 |
0 |
|
|
NUMBER |
|
931 |
0.000 |
|
0.000 |
1 |
0 |
0 |
0 |
0 |
|
|
QUEUE |
|
MAX CONT. ENTRY ENTRY(0) AVE.CONT. AVE.TIME |
AVE.(-0) |
|
||||||||
RETRY |
|
|
|
|
|
|
|
|
|
|
|
|
LINE |
|
2 |
1 |
4589 |
|
2695 |
0.252 |
5.489 |
13.299 |
0 |
||
FEC XN |
PRI |
BDT |
|
ASSEM |
CURRENT |
NEXT |
PARAMETER |
VALUE |
|
|
||
4 |
0 |
100010.314 |
4 |
|
3 |
4 |
|
|
|
|
|
|
1 |
0 |
100030.170 |
1 |
|
8 |
9 |
|
|
|
|
|
|
1004 |
0 |
100100.000 |
1004 |
|
0 |
11 |
|
|
|
|
|
|
Вероятность исправной работы системы (коэффициент готовности) равна 0.931 !
Индивидуальные задания на работу №4
Исследовать надежность системы с восстановлением с горячим и холодным резервированием всеми перечисленными выше способами со следующими исходными данными:
n – номер варианта;
- интенсивность отказов [единиц/час];
s – количество устройств в системе (рабочее и резервные) μ – интенсивность восстановления [единиц/час].
27
n |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
|
|
|
|
|
|
|
|
|
|
0.04 |
0.05 |
0.06 |
0.07 |
0.08 |
0.08 |
0.08 |
0.1 |
0.1 |
0.1 |
|
|
|
|
|
|
|
|
|
|
|
s |
2 |
3 |
3 |
3 |
4 |
4 |
4 |
3 |
4 |
4 |
|
|
|
|
|
|
|
|
|
|
|
μ |
0.05 |
0.06 |
0.07 |
0.08 |
0.09 |
0.1 |
0.05 |
0.06 |
0.07 |
0.08 |
|
|
|
|
|
|
|
|
|
|
|
Требования к оформлению отчета
Отчет должен соответствовать стандарту СТО ИрГТУ. 005 – 2007 Оформление текстовых и графических материалов студентами.
Контрольные вопросы.
1. В чем заключается сущность метода восстановления?
2.Есть ли достоинства у данного метода ?
3.Чем отличаются программы имитационного моделирования систем с восстановлением от систем без восстановления?
4.Можно ли для анализа систем с восстановлением использовать уравнения Колмогорова ?
5.Чему будет равна вероятность исправной работы системы в установившемся режиме, если интенсивность выхода элементов из строя λ будет превышать интенсивность восстановления μ?
Литература
1.Е.С. Вентцель, А.А. Овчаров. Теория вероятностей и ее инженерные приложения.
М.: “Наука” ,1988 г.
2.Т.Дж. Шрайбер. Моделирование на GPSS. М.: Машиностроение, 1980 г.
3.Надежность АСУ / под ред. Хетагурова - М.:Высш. Шк., 1979 г.
4.А.И. Плис, Н.А. Сливина. MATHCAD 2000. М.: Финансы и статистика,2000 г.
5.Ю.П. Хрусталев. Моделирование систем массового обслуживания. Из-во ИрГТУ,
2007
6.СТО ИрГТУ. 005 – 2007. Оформление текстового и графического материала студентами.
28
